Lesson 2

Cover Up: Fact Families

Est. Class Sessions: 1

Developing the Lesson

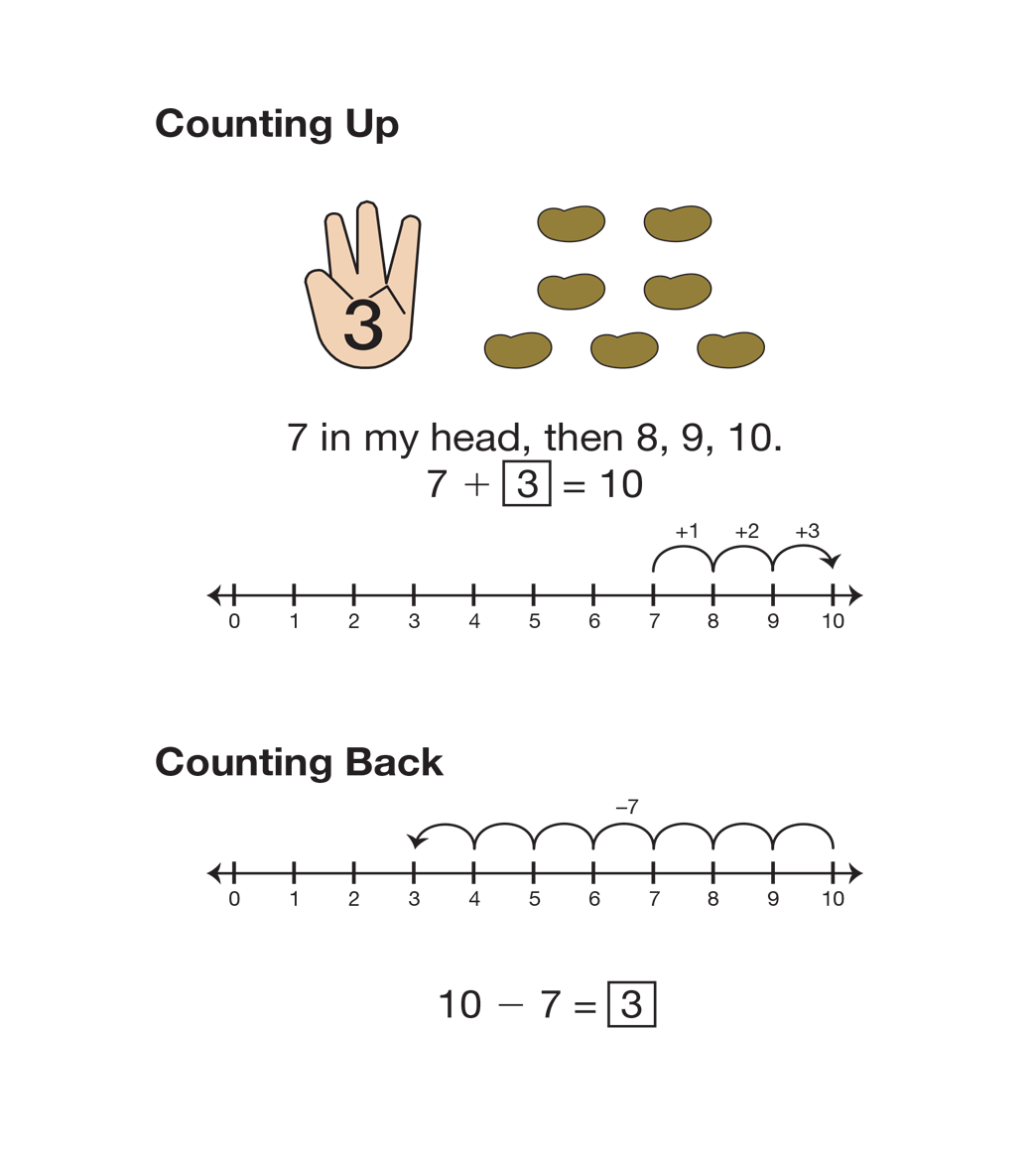
Solve a “Cover-Up” Problem. Display 10 beans. Ask students to count the beans. Cover up several beans. Make sure students do not see how many you cover. Ask students to determine the number of beans you have covered by looking at the beans that are left over. Students can use a variety of strategies to solve this problem. For example, if seven beans are left, a student might use the counting-up strategy to determine the number hidden. Other students may choose to use their desk number lines or other manipulatives to count back. See Figure 1.

Ask students to share their strategies. As students volunteer their strategies, ask other students to explain the same strategy in their own words.

After students share their solution strategies, ask them to describe the problem with a number sentence. Write the number sentences in a column on the board or other display. Ask students for more than one number sentence. For example, one student may suggest 7 + 3 = 10, while another gives 10 − 3 = 7.

Write both on the display and ask:

X
  • What do you notice about these two number sentences? Do you notice anything that is the same? (They both have the same numbers in them.)
  • What is different? (The numbers are in a different order. One is an addition sentence and one is subtraction.)
  • Are there other number sentences that we can write using these three numbers? What are they? (3 + 7 = 10 and 10 − 7 = 3)

Ask volunteers to tell a story for 10 − 3 = 7 and 10 − 7 = 3 using beans and then ask students to show how to solve these problems on the class number line.

Then use the following prompt to help students confront common mistakes when writing fact families:

X
  • What if I change the order in which these subtraction section sentences are written?

Add 3 − 7 = 10 and 7 − 10 = 3 to the display in a second column next to the other four previously written then ask:

X
  • Use the beans to tell your neighbor a story that matches 3 − 7 = 10 or 7 − 10 = 3.
  • What do you notice about your stories? (They don’t work or make sense. I can’t take more away than I have.)
  • Can someone show us on the class number line how to solve these number sentences? (Possible response: They won’t work. If there’s only 3 of something there are not enough to take 7 away. If you have 7 things, there’s not enough to take 10 away. When I solved 3 − 7 = 10 I landed below zero on the number line.)
  • How are the subtraction sentences in the first column different from those in the second column? (Possible response: The number sentences in the second column are not true.)
  • We call the four number sentences in the first column a “fact family.” Why do you think we call them a “family”? How are they like a family? (Possible responses: They all use the same numbers and families have the same name; they belong together; they look alike but they are different sentences.)
  • Would it be helpful to know the other members in a fact family? Why? How could it help you? (Knowing an addition fact can help you solve a subtraction problem. It can also help you solve the turn-around fact. For example, 3 + 5 = 8 and 5 + 3 = 8.)

Pose several other cover-up problems covering up different numbers of beans. Each time, ask students for all the number sentences in the fact family and write them on display.

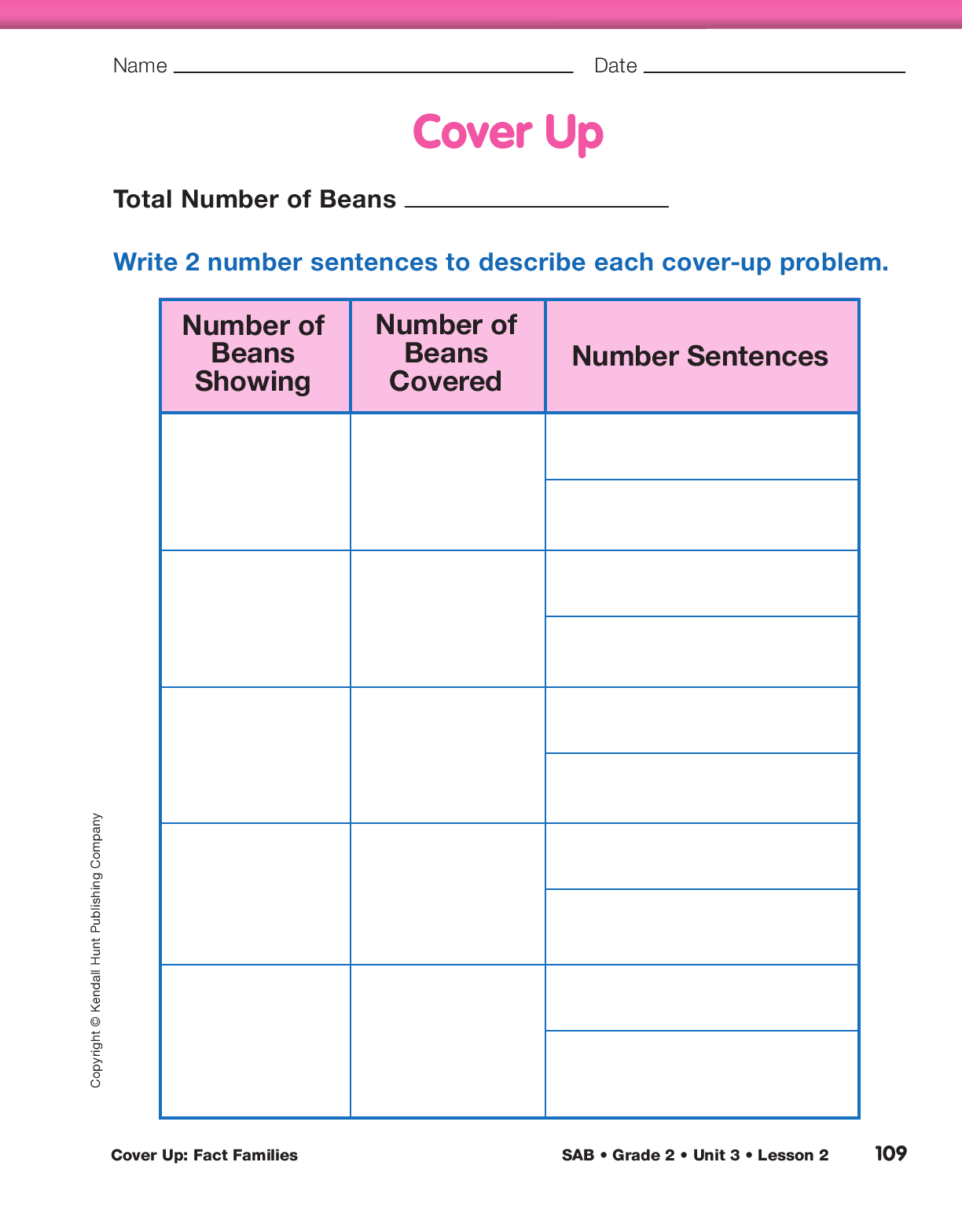
Demonstrate and Play Cover Up. Display the first page of the Cover Up pages in the Student Activity Book. Distribute
20 beans to each student pair. Students should record the total number of beans they are using at the top of the Cover Up page. They can use any number they choose from 9 through 20. Encourage students to take turns being “Hiders” and “Detectives” in a game of Cover Up. One student hides a number of beans while the other tries to determine the number of beans covered. Both students record the number of beans showing and the number of beans hidden on their Cover Up page. They write a number sentence for each problem and then write a different number sentence that is in the same fact family. Use the display to demonstrate a round. See Figure 2.

While students play Cover Up, observe the use of various solution strategies. Elicit other number sentences that describe the same problem. Encourage students to repeat the game by choosing a different starting number. A second game page is provided.

X

Assigning higher or lower numbers to various groups playing Cover Up may be appropriate to enable students to play successfully. For example, by providing extra beans, students who are comfortable can play using larger starting numbers.

ADVENTURE BOOK:
Student Activity Book: 109
X
SAB_Mini
+
Master:
Solving a “cover-up” problem
X
+
Sample recordings in Cover Up game
X
+