Exploring Numbers
Number Sense and Operations

This unit introduces ideas associated with number sense and numeration. Some of the … read more
This unit introduces ideas associated with number sense and numeration. Some of the activities involve mathematics
in real-world contexts. Others are simply numerical explorations. These activities will strengthen students’
background for work with numbers in
future units.
The mathematical topics introduced here will be revisited during the course of the year. We do not expect mastery of the topics during this unit, nor is mastery required for subsequent work. Rather, we expect students to show growth with continued exposure over time.
Topics covered in this unit include writing number sentences that have more than one addend on each side of the equal sign, problem solving involving addition and subtraction, working with data, skip counting, exploring and comparing numerical patterns on number charts and number lines, and recognizing even and odd numbers. Math tools, such as the 200 Chart, number line, and coins are used. Students investigate a problem using the TIMS Laboratory Method. Students will also read an Adventure Book story about a boy who solves a problem in the grocery store using strategies he explored in class.
Subtraction Concepts
This unit builds subtraction concepts, language, and skills that help students make sense of … read more
Subtraction Concepts
This unit builds subtraction concepts, language, and skills that help students make sense of subtraction situations in order to solve problems. Lesson 3, Explore Subtraction Word Problems, focuses on two of the three types of subtraction situations, Separate/Take Away and Compare. The three main types of problem situations that can be represented by 9 − 5 = ? are illustrated in Figure 1. It is important that students encounter multiple examples of each of these subtraction situations so that they can learn to choose appropriate strategies and tools to solve all kinds of problems. Students need not learn to identify or name the types of problems. Rather, they need to learn to approach all types of problems with confidence. As students work on problems, focus on the way they reason to find answers and on the language and representations they use to describe their thinking.
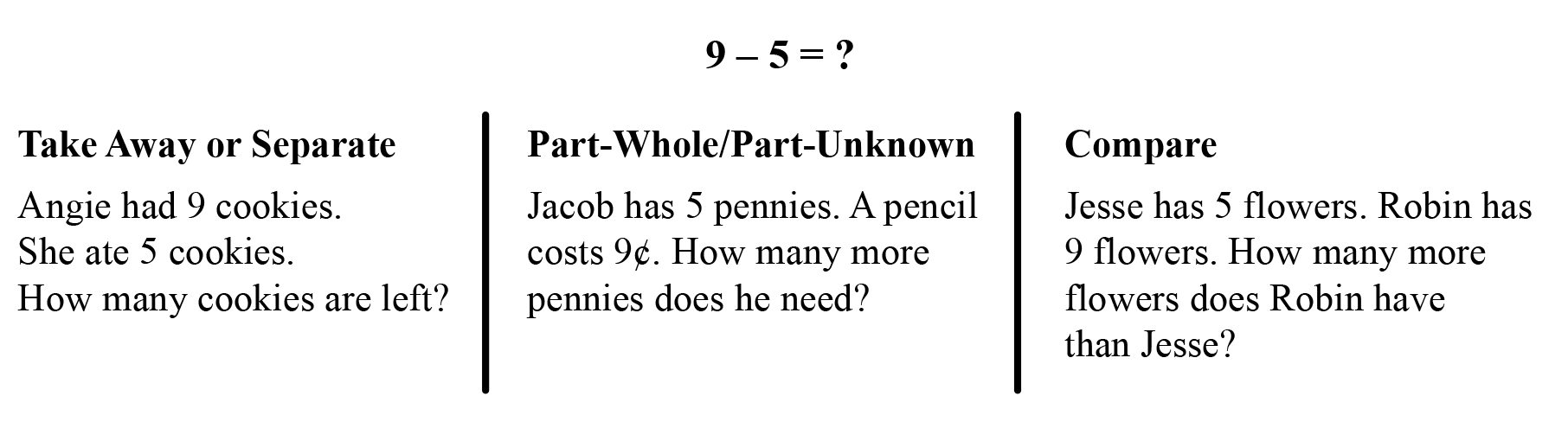
Figure 1: Problem types represented by 9 − 5 = ?
Developing Addition and Subtraction Strategies
In accordance with the National Council of Teachers of Mathematics … read more
Developing Addition and Subtraction Strategies
In accordance with the National Council of Teachers of Mathematics Principles and Standards for School Mathematics, the Curriculum Focal Points (NCTM 2000, NCTM 2006) and the Common Core Standards for Mathematics, Math Trailblazers students are expected to achieve fluency with the addition and subtraction facts by the end of second grade. Students work toward this goal by solving addition and subtraction problems in ways that make sense to them. Students also approach the math facts by systematically developing efficient strategies for the facts that will help them learn other facts.
In Unit 3, students use mental math strategies and reasoning strategies to solve addition and subtraction problems within 20. Students come to understand the concept of addition by interpreting and finding strategies to solve different types of problems (e.g., join, separate, compare, and part-whole). As they do, they also develop greater fluency with each specific counting strategy. Significant research from all over the world indicates that children move through a progression to find the sum of single-digit numbers. First, children count all objects, then count on, and then they reason the sum from known facts. (National Research Council, 2001)
Students practice using the following mental math strategies and reasoning strategies to solve both addition and subtraction problems within 20:
- Using Doubles: I know 7 + 7 = 14 and 14 − 7 = 7, so 15 − 7 is 8.
- Using Ten: I know 20 − 10 = 10; For 20 − 9, I take off one less, so it is 11.
- Making Ten: 17 + 3 = 20; I can make a 10 with 7 + 3 and add another ten. 7 + 3 + 10 = 20.
- Reasoning from Known Facts: I know 13 + 4 is 17 because I know 13 is a ten and 3 ones. 4 ones plus 3 ones is 7 and then I add the ten.
In Unit 3, students solve subtraction problems using counting strategies. The learning progression for subtraction is similar to that of addition. Students invent counting back strategies that model the taking away problem situation. Some invent counting-up strategies for some compare or missing addend situations. Focusing students on part-part-whole relationships also helps students develop reasoning strategies, especially for subtraction. These experiences help students connect addition and subtraction and help them recognize when to add and when to subtract. “For students in grades K to 2, learning to see the part-whole relations in addition and subtraction situations is one of their most important accomplishments in arithmetic.” (National Research Council, 2001)
Subtraction Facts Strategies
A number of strategies are useful for gaining fluency with the subtraction facts. Strategies related to … read more
Subtraction Facts Strategies
A number of strategies are useful for gaining fluency with the subtraction facts. Strategies related to counting are particularly good for young children. They provide a foundation for more complex fact strategies. However, in Second Grade, students should begin developing more efficient strategies such as reasoning from known facts (i.e., thinking addition).
Problems in this unit encourage the following strategies:
- Counting Up. Counting up involves counting from the known part to the whole. For the problem, 5 + ______ = 8, start with five (the known part) and count up to eight (the whole), “six, seven, eight.” You counted three more, so the answer is three.

The thinking involved in counting up is similar to that used when adding. This encourages students to use addition thinking for subtraction facts. Although it could be used with any subtraction problem, counting up is most useful when the two numbers are close to each other, e.g., 30 − 28.
- Counting Back. Counting back involves starting with the whole and counting back the amount of the known part. For the problem, 9 − 2 = ______ , start with nine (the whole) and count back two from 9: “8, 7.” Since you stopped counting at seven, the answer (or other part) is seven.

Although this strategy can be used for many subtraction problems, it is most often used when the known part is a small number, such as one, two, or three, e.g., 50 − 2.
- Thinking Addition. Students’ initial approach to finding the answer to a subtraction fact such as 9 − 5 is to show nine fingers, fold down five, and count the remaining ones. While this works with small numbers, it is cumbersome with larger numbers. A more mature strategy uses the relationship between addition and subtraction to organize numbers and to provide a way of thinking of the subtraction facts.
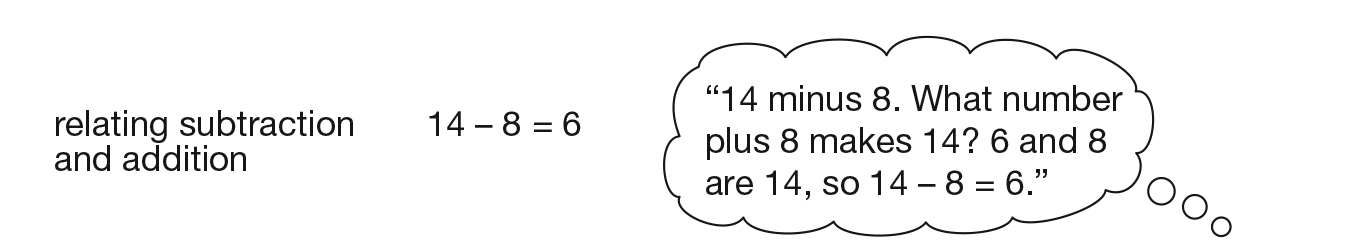
Connecting Addition to Subtraction
There are many opportunities in this unit to connect addition to … read more
Connecting Addition to Subtraction
There are many opportunities in this unit to connect addition to subtraction.
In Lesson 2, Cover Up: Fact Families, students practice writing related addition and subtraction sentences.
The modeling and discussion of the relationship between addition and subtraction is important. In this
lesson, students “think addition” to solve subtraction situations. In the “Cover Up” activity, the beans for the
unknown part of the equation are left hidden under cover and students are encouraged to think about the hidden
part. They need to think about the quantity that needs to go with the number of beans they see to make
the whole, for example, “What goes with 7 to make 15?”
See Figure 2.

Figure 2: Thinking addition in the Cover Up game to solve 15 − ? = 7
Representations
Students are introduced to the 200 Chart in Lesson 5. In Lesson 6, they use the chart as well as … read more
Representations
Students are introduced to the 200 Chart in Lesson 5. In Lesson 6, they use the chart as well as counters, drawings, and number lines to solve word problems involving two whole numbers with a sum within 100. Two games, Moving on the 200 Chart and Moving on the Number Line, practice adding and subtracting using these representations. See Figures 3 and 4. Students also use the 200 Chart to identify and describe patterns, and to represent quantities like they did with number lines and number sentences. Comparisons are made between the number line and the 200 Chart. Students are asked to identify patterns and moves on the 200 Chart and then to represent them on the number line.
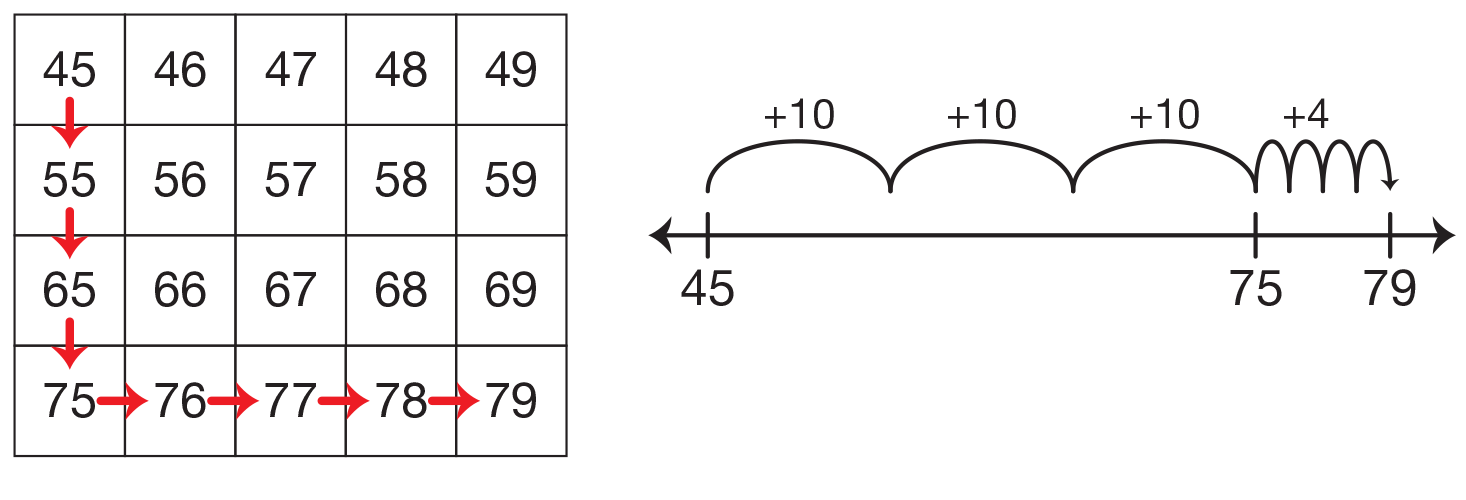
Figure 3: Using the 200 Chart and number line to solve 45 + 34
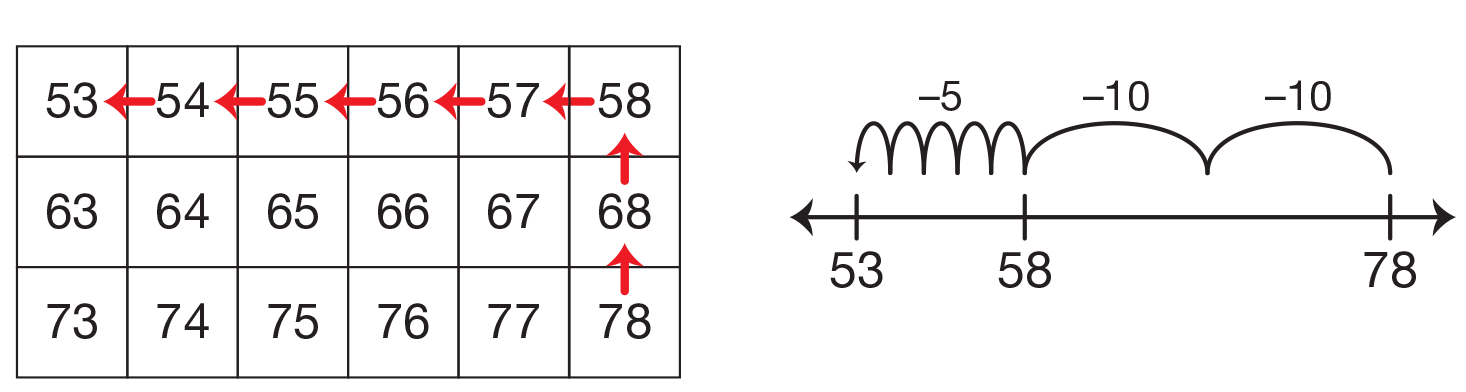
Figure 4: Using the 200 Chart and number line to solve 78 − 25
Equal Sign
Students learn to recognize that the equal sign represents the relationship between two … read more
Equal Sign
Students learn to recognize that the equal sign represents the relationship between two equal quantities. The equal sign is one of the most important symbols in mathematics, yet it is often poorly understood. Students often misunderstand the equal sign to mean “the answer comes next.” With practice, students learn to see that both sides of the equal sign are equivalent equations. In Lesson 1, Number Sentences for Tile Designs, students write several different number sentences for square-inch tile designs. They discover that in a true number sentence, whatever is on one side of the equation equals whatever quantity is on the other side. Students compare the results on one side of the equal sign to the results on the other side and determine if they show equivalent quantities and identify the number sentences as true or false. This important concept will support algebraic thinking in future grades.
TIMS Laboratory Method
In Lesson 4, Our Favorite: A Data Collection Lab, students use the … read more
TIMS Laboratory Method
SIn Lesson 4, Our Favorite: A Data Collection Lab, students use the TIMS Laboratory Method to graph and explore data collected in the classroom. They use strategies to solve addition and subtraction problems based on that data such as “How many more students chose peanut butter and jelly sandwiches than ham sandwiches?”
MATH FACTS and MENTAL MATH

Addition Facts with Sums to Ten
In this unit, students continue to systematically review the … read more
Addition Facts with Sums to Ten
In this unit, students continue to systematically review the addition facts. Daily Practice and Problem items in this unit can be used to assess students’ fluency with the addition facts with sums to ten in Group D (3 + 3, 3 + 4, 4 + 4, 4 + 5).
Students should also be developing reasoning strategies to solve the addition facts with sums larger than ten in
Group D (6 + 6, 6 + 7,
7 + 7, 7 + 8, 8 + 8, 10 + 9, 10 + 10). Direct modeling, counting strategies, or reasoning
from known facts strategies are commonly used to solve these facts.
Fact Families for Addition Facts with Sums to Ten
Students have been connecting addition to subtraction and using the addition facts to … read more
Fact Families for Addition Facts with Sums to Ten
Students have been connecting addition to subtraction and using the addition facts to solve subtraction problems since First Grade. A student proficient with his or her addition facts can also find the related subtraction facts. Daily Practice and Problem items in this unit can be used to assess students’ abilities to name the fact families related to each fact with a sum to ten in Group D. As students develop fluency with the facts with larger sums, they will be able to name the related facts in the fact family.
Resources
- Carpenter, T.P., D.A. Carey, and V.L. Kouba. “A Problem-Solving Approach to the Operations.” In Mathematics for the Young Child. J.N. Payne, ed. National Council of Teachers of Mathematics, Reston, VA, 1990.
- Carpenter, T.P., E. Fennema, M.L. Franke, L. Levi, and S.E. Empson. Children’s Mathematics: Cognitively Guided Instruction. Heinemann, Westport, CT, 1999.
- Carpenter, T.P., and J.M. Moser, “The Acquisition of Addition and Subtraction Concepts in Grades One through Three.” In Journal for Research in Mathematics Education, 15 (3), pp. 179–202, 1984.
- Isaacs, A.C., and W.M. Carroll. “Strategies for Basic-Facts Instruction.” In Teaching Children Mathematics, 5 (9), pp. 508–515, 1999.
- National Research Council. “Developing Proficiency with Whole Numbers.” In Adding It Up: Helping
Children Learn Mathematics,
pp. 181–229. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001. - Principles and Standards for School Mathematics. National Council of Teachers of Mathematics, Reston, VA, 2000.
- Professional Standards for Teaching Mathematics. National Council of Teachers of Mathematics, Reston, VA, 1989.
- Thornton, C.A. “Emphasizing Thinking Strategies in Basic Fact Instruction.” In Journal for Research in
Mathematics Education,
9 (3), pp. 214–227, 1978. - Thornton, C.A. “Strategies for the Basic Facts.” Mathematics for the Young Child. In J.N. Payne, ed. pp. 133–151. National Council of Teachers of Mathematics, Reston, VA, 1990.












