Lesson 3

Doubles

Est. Class Sessions: 2–3

Developing the Lesson

Part 2. Graphing the Doubles

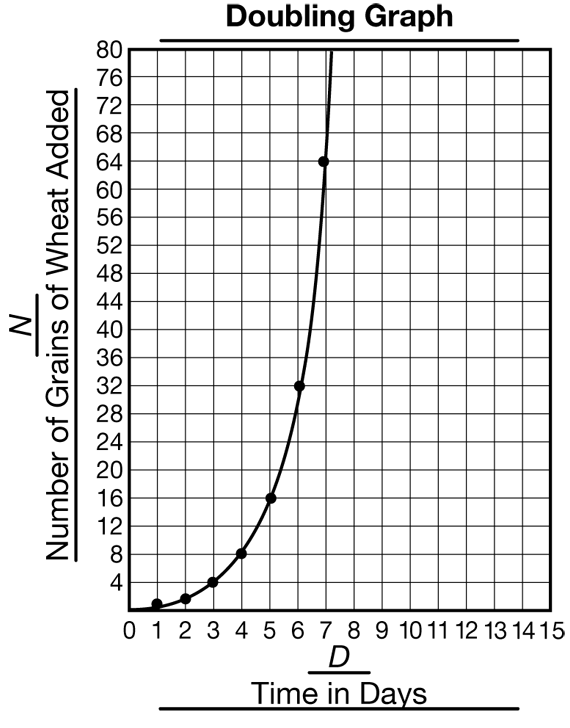
Question 7 asks students to make a point graph on copies of the Centimeter Graph Paper Master. They graph the number of days (D) on the horizontal axis and the number of grains of wheat added each day (N) on the vertical axis. Students should see that as the number of days gets larger, the number of grains added gets much larger. The points form a curve. When you discuss the question, use a display of the graph to show students how to sketch the curve using the points on the graph. Encourage students to tell a story for their graph. A sample graph is shown in Figure 5.

Ask students:

X
  • On what day does your graph run off the paper? (Day 8 using the scale shown in Figure 5)
  • If you taped another sheet of graph paper at the top of your graph, how many more days would you be able to graph before running off again? (1 day; the point for Day 8 is 128 grains of wheat; another sheet of graph paper will accommodate points up to 160 grains of wheat added.)
  • About how many sheets of graph paper would you need to graph the number of grains of wheat added on Day 10? Day 11? (7 sheets of graph paper; 13 sheets of graph paper)

Assign the Homework section in the Student Guide. Students will need the Math Practices page in the Reference section of the Student Guide.

X

Stories. There are many versions of the story told in the Doubles pages in the Student Guide about the grains of wheat on the chessboard. Two good resources for the story are Chapter 1 of One, Two, Three . . . Infinity by George Gamow and “Pastimes of Past and Present Times” in Volume Four of The World of Mathematics edited by James R. Newman. For complete references for these books, see the Mathematics in this Unit. Other versions for children are described in the Extensions for this lesson.

To fulfill his promise, the king needed 264 − 1 or 18,446,744,073,709,551,615 total grains of wheat. This is eighteen quintillion, four hundred forty-six quadrillion, seven hundred forty-four trillion, seventy-three billion, seven hundred nine million, five hundred fifty-one thousand, six hundred fifteen grains of wheat. According to James Newman this is “enough to cover the surface of the earth to the depth of the twentieth part of a cubit.” (One twentieth of a cubit is about one inch.)

In a different version of the story, the vizier asked for payment in grains of rice. One estimate is that a stack of 264 − 1 grains of rice would reach one-quarter of the way to the nearest star after the sun.

Student Guide:
Student Activity Book:
Master:
A sample graph
X
+