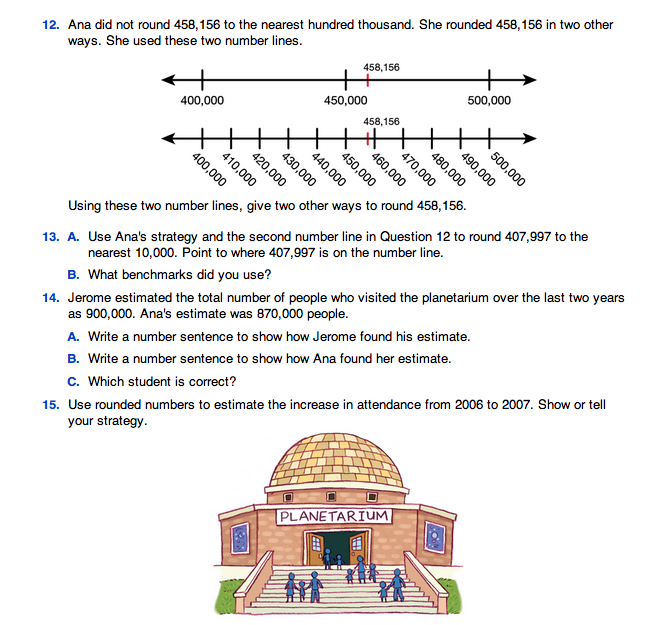
Using Estimation

Est. Class Sessions: 2–3

Developing the Lesson

Part 1: Mystery Jars

Discuss Estimation. To begin the activity, discuss the opening example and Questions 1–2 in the Mystery Jars section in the Student Guide. Students must estimate the number of birds in a larger picture when given the number of birds in a smaller picture. Give students a few minutes to discuss with a partner how to make an estimate. Have students describe their estimation strategies. Highlight strategies that include estimating the number of times the small picture will fit into the larger picture (about 5 times), then multiplying this estimate by the number of animals in the smaller picture (about 25 birds). Since 5 × 25 = 125 birds, 125 birds is a good estimate. Point out that a similar method is used to estimate the size of a crowd at concerts, sports events, and political rallies.

Ask:

Do you think your estimate is exactly the same as the total number of birds in the larger picture? Why or why not? (Students may discuss possible reasons that the estimate is inexact. For example, the number of birds in a smaller rectangle may vary when taken from different parts of the larger picture. The number of times the smaller picture fits into the larger picture may also be an inexact number. Further, some birds are only partially shown in the pictures.)
If Linda wanted to know the total number of birds in a whole flock flying through the sky, should she try to find an exact number or should she estimate? (She should estimate. It would be difficult or impossible to count an exact number of moving birds in a large flock.)

Read and discuss Questions 3–4 in the Mystery Jars section of the Student Guide.

What's close enough? For seeing patterns in data and in many of the hands-on experiments in Math Trailblazers, 10% is about the accuracy we can expect from students given the equipment they'll use and situations with which they'll be presented. For example, using 10% as a rough standard of closeness, estimates of 90–110 for a jar containing 100 objects would be considered close enough.

Use Estimation. To help students think through the estimation process, choose one of the prepared mystery jars. See Materials Preparation. Ask students to estimate the number of objects in the jar.

Show the class the bag containing the reference number of objects that corresponds with the mystery jar.

For example, if the reference bag has 100 objects, say:

Here are 100 objects. Estimate the number of objects in the mystery jar.
Do you think there are more than 10 or less than 10 objects in the mystery jar? Why do you say so?
How does the reference bag help you?
Do you think there are more than 100 or less than 100 objects in the mystery jar? Why?
Do you think there are more than 500 or less than 500 objects? Why? How does the reference bag help you decide?

Discuss possible estimation strategies. Highlight strategies that utilize the reference bags and involve the rudiments of proportional reasoning. Then tell students that they will estimate the number of objects in each of the mystery jars. Have students begin a data table by drawing a Three-Column Data Table as shown in Figure 1.

If you have a large class, you can reduce the “bunching up” at the stations by creating a few more mystery jars and having more stations.

Make Estimates. Place the other prepared mystery jars at various stations throughout the room. Allow students to circulate throughout the room and make their estimates. They should identify each jar by number in their data tables and fill in the type of object and their estimates.

Analyze Estimates. When students have finished making their estimates, open the lids and tell the exact number of objects in each jar. Record the actual quantities on the board or another display. The following discussion prompts use the estimates in the data table in Figure 1 as examples. Use the prompts to help guide a discussion on what it means to be close.

Open the larger jar that contains the same objects as a smaller jar. The following discussion prompts are based on Jar 2 in Figure 1. Tell the class the actual number of objects in the larger jar.

Ask:

Who has an estimate that matches the actual number exactly? (Chances are good that very few, if any, of the students will be able to guess the exact number of objects.)
Who has an estimate that is close? (More students will be able to say that their estimates are close.)
Which estimates are close enough to the actual number to be good estimates? How much larger or smaller can your estimate be and still be a good estimate?
How can we decide whether an estimate is close enough or not?

If you do not have the space on the board for the number line, list all the estimates in your class in order from smallest to largest and place the actual quantity in the list at the appropriate place.

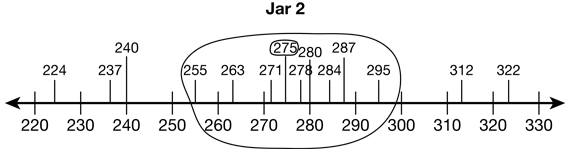
If you have the space on the board, draw a number line that encompasses at least 100 units on either side of the actual number of objects in the jar. Insert appropriate benchmarks. Mark the actual number of objects that are in the jar on the number line. Have students place their estimates on the number line. See Figure 2. When the estimates have all been inserted into the number line, initiate a discussion with students about the range shown.

Ask:

Look at the estimates on the number line and describe where they fall. (Possible response: They are between 224 and 322. There are several estimates that are close to the actual number, 275.)
Are they larger or smaller than the actual number in Jar 2?
How close are the estimates to the actual number in Jar 2?
Are there a lot that are close or only a few?
How can we decide which estimates are close enough to the number of beans in Jar 2 and which ones we think are too far away?
Where would you draw the lines between good enough estimates and estimates that are not close enough? Give the reasons why you think so.

Analyze with the class whether the estimates cluster around the actual number of beans in Jar 2 or if they are more spread out. If there is an identifiable cluster, draw a circle or lines separating the cluster from those farther away. See Figure 2. Suggest that the estimates within the cluster can be considered close enough and those outside the cluster not close enough.

Using the hypothetical estimates listed in Figure 2, it may be reasonable to draw lines to identify the estimates 255 through 295 beans as the range of close estimates and those outside of that range as not close enough. Both estimates are 20 units away from the actual number and for both numbers there is a gap before the next closest estimate.

If there has been no identifiable cluster around the exact number, have the students discuss where to draw the lines between the estimates they think are close enough and those not close enough.

Choose the smaller jar filled with the same objects and tell the class the actual number of objects in the jar. For the purposes of this discussion, we'll refer to Jar 3 listed in the table in Figure 1. Conduct the same discussion about this jar as for the larger jar. Draw another number line and insert the students' estimates in order, along with the actual number of objects in that jar.

Ask:

Whose estimates match the actual number exactly?
Whose estimates are close?
Which estimates are close enough to the actual number to be good estimates? How much larger or smaller can your estimate be and still be a good estimate?

At first students may choose the same range of values as they did for the larger jar. For example, if there are actually 25 beans in the jar, students may say that good estimates may also be within about 20 of the exact number. However, other students may feel that estimates as low as 5 and as high as 45 beans are not good estimates.

Ask:

Do you think that it makes sense to judge our estimates for both the large and small jars using the same range (a range of about 40 objects)? (No, when there are a large number of objects you can have a larger range. When there are only a small number of objects you need a smaller range.)

It is clear that we cannot use a difference of 20 objects as our standard for both Jars 2 and 3. Estimates within 20 beans of 275 beans, such as 295 beans, can be considered good estimates. Using the same range, however, for the number of beans in Jar 3 is not appropriate. Estimates as low as 5 and as high as 45 beans should not be considered good estimates when the actual number is 25 beans.

Ask questions such as:

Do you think that guessing a number that is 20 away from 25 beans is as good an estimate as guessing a number that is 20 away from 275 beans? Why or why not? (Possible response: In the little jar you can tell there are more than 5 beans, because you could just count them. You can guess closer with smaller jars. Large jars are harder to guess, so you could be further away.)
What is different about the two estimates, even though they are both just 20 away from the right number? (The one for the larger number of beans is more accurate. The error should be smaller when the number of objects is smaller.)
Is it easier to estimate when there is a small number, such as in Jar 3, or a large number as in Jar 2? Why do you think so? (Possible response: I think it is easier to estimate when there is a small amount because you can actually see more of the the items. When there are a lot of items more of them are packed in.)
If there are 474 students in the school, is an estimate of 500 (26 away from 474) students close enough? (In many situations, yes.)
Why do you say so? (Possible response: If you need to know how much paper to order for the school, an estimate of a little more will make sure you have enough.)
If there are 27 students in the classroom, is an estimate of 1 (26 away from 27) student close enough? Why not? (No, because you can tell there is a lot more than 1 student. If you needed to buy paper for the class, buying for one person is not enough.)
What happens to the range of acceptable estimates as the numbers get larger? (The range gets larger.)
What happens to the range when the actual numbers get smaller? (The range gets smaller.)

How Close is Close Enough? Have students work in pairs to discuss and answer Questions 5–9 in the Student Guide. Alternatively, Questions 5–9 can be assigned as homework after Part 1.

Question 5 asks students to estimate the number of people in the crowd watching a basketball game. Encourage them to use the number of people in the small picture as a reference number. As students report their estimates to the class, encourage them to explain their estimation strategies. How can we know if our estimate is close enough? In this case we may have to be satisfied with knowing that we have used good strategies to make the estimates since it would be difficult to count each person. There are approximately 900 people in the picture.

In Questions 6–8, students review the notion of relative error by analyzing the estimations that Linda and Romesh make for the mystery jars in their classroom. Provide students with an opportunity to answer these questions with a partner and then use the following questions help to guide the discussion:

Ask:

Linda's estimates for the number of marbles and the number of marshmallows are both 12 away from the actual numbers. Why is her estimate for the number of marbles a better estimate than her estimate for the number of marshmallows? (Linda's estimate for the marbles is better because there are a lot more marbles in the jar. Making an estimate that is 12 away is pretty close. Since there are only 38 marshmallows in the jar, an estimate of 50 is way too big. Your estimate should be much closer to 38.)
Look at the estimates that Linda and Romesh made for the number of marbles in the first jar. Which one made a better estimate? (Linda) Explain how you decided? (Linda is only 12 away on her estimate and Romesh is 22 away.)
Look at their estimates for the number of marshmallows. Who made a better estimate? (Romesh) Explain how you decided. (Romesh is much closer in his estimate. He is only 3 away from the actual number, but Linda is 12 away.)

In Question 8A, students should see that both Linda and Romesh made reasonable estimates. Linda's estimate is 13 away and Romesh's estimate is 12 away but both are reasonable. In Question 8B, Romesh's estimate is closer to the actual number.

Question 9 asks students to determine whether or not given estimates are reasonable. Students should consider the context for each estimate. In Question 9A, the estimate is too low to be reasonable. In this situation, the estimate needs to be very close (perhaps within one-half of a centimeter of the measured width of the opening, but not greater than the width of the opening) for the door to fit properly. In Question 9B, the estimate is also too low. Keenya will not have enough money to pay for the actual cost of the groceries. Although the estimates in Questions 9C and 9D are both within 9 of the actual number, their reasonableness has to do with the relative size of the error compared with the estimated number. The difference in Question 9C is small compared to the actual number, so the estimate is more reasonable than in Question 9D, where the error is large compared to the actual number.

Show students the additional mystery jar you prepared before class. Also display the reference bag with 50 of the same objects that are in the mystery jar. Put the jar in a place where students can look closely at it. Make sure the reference bag is marked to show the number of objects it contains. Ask:

How many objects do you think are in the mystery jar?
Make an estimate and write it in your journal.
Pretend you are writing to one of your classmates. Explain to him or her in your journal how you made your estimate.
Explain how close you think your estimate is to the actual number. Explain your reasoning.

Use the Journal Prompt to assess students' abilities to estimate quantities [E7]. Additional practice with mystery jars can provide continued targeted practice.