Big Base-Ten Pieces

Use Place Value Chart II. Discuss the size relationships of the base-ten pieces using the discussion prompts below and the display of the Place Value Chart II Master.

Build a Super Skinny. A student will likely suggest that ten packs taped together in the shape of a skinny will show 10,000. If they do not, repeat the demonstration showing how ten bits connected together to make a skinny. Have students count by thousands as the ten packs, or super bits, are placed together to form a model of 10,000. Demonstrate how ten packs fit the length of a meterstick as you move one pack from one end to the other. See Figure 6.

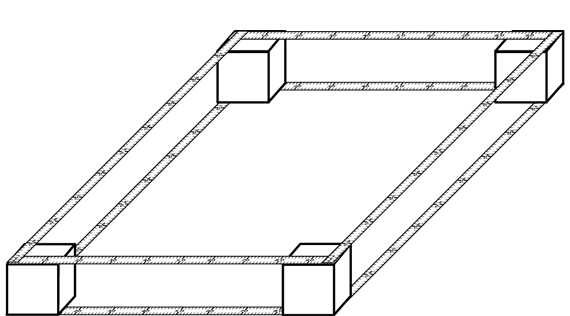
After this demonstration, you and the students can construct a physical model of 10,000 as shown in Figure 7. You will need two packs and four metersticks. Have students help you place the packs one meter apart on a table or on the floor. Use the four metersticks to make the edges of your model by placing two of the sticks from pack to pack on the top and two of the sticks from pack to pack on the bottom. Tape the sticks in place and, if possible, cover your model with paper so that it more closely resembles the other base-ten pieces. Name this model a super skinny.

Ask a student to record the 10 × 1000 relationship in the Ten Thousands place on the Place Value Chart II master as shown in Figure 5. Call attention to the two patterns that are evolving. The first pattern is the shapes: bit (one), skinny (ten), flat (100), super bit (1000), super skinny (ten thousand). The second pattern is that each number is 10 times larger than the number to its right.

Build a Super Flat.

Students will likely see that 10 of the super skinnies will make a super flat. Have students build a model using four packs and eight metersticks. Lay down four metersticks to form a square. Place one pack in each corner of the square and tape the meterstick and packs together. Students can help you place the other four metersticks along the top edges to form a square. Tape these in place. If possible, cover the model with paper so that it resembles a flat. See Figure 8. Emphasize that the super flat model represents 10 super skinnies or 100 packs, just as the flat represents 10 skinnies or 100 bits. Ask two students to place the super skinny at one end of the super flat. Have students count by 10,000s as they move the super skinny from one end of the super flat to the other. (10,000; 20,000; 30,000 … 100,000).

Build a Megabit. Return to the Place Value Chart II Master and have a student record 10 × 10,000 in the Hundred Thousands column.

Record 10 × 100,000 in the One Millions column. Emphasize the pattern of 10 times the number to the right. See if students can identify the shape of the model that will continue the pattern of the models of the base-ten pieces. If students are not able to identify the cube, go back to the ones cube and name each shape as you move through the place value chart (bit, skinny, flat) until they are able to identify the shape as a bit (cube). Name this model a megabit.

Guide students to see that ten of the super flats stacked will make a megabit that is a cube that measures 1 meter × 1 meter × 1 meter. Have students count by 100,000s to 1 million as you use your hands to pretend to stack 10 super flats.

To build a megabit, you need 12 metersticks. Have students help in the construction of the megabit by holding the sticks in place as someone tapes them together. To construct this cube, place four metersticks on the floor in a square. Use four more metersticks to build the edges of the sides by placing one meterstick perpendicular at each corner. Use tape to hold these sticks together. You can use rulers and packs to brace each corner on the bottom of the megabit. Now place the last four sticks in a square on top of the four “sides.” Use tape to hold these together. If possible, cover the megabit with paper. See Figure 9.