Using Estimation

Remove the articles and sources displayed on the Newswire Numbers bulletin board in Lesson 2. Divide students into small groups and give each group a share of the news items. Ask each group to sort the articles into two categories—those that appear to be exact numbers and those that appear to be rounded numbers. Remind students that a rounded number is a number that is close to the exact number, but is expressed to the nearest ten, hundred, thousand, etc.

Direct students to the It's About . . . section in the Student Guide.

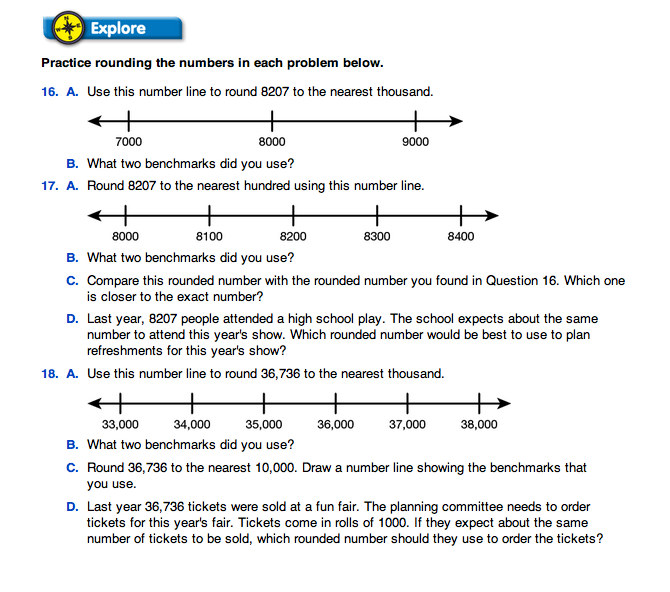
Discuss students' solution strategies. Then, introduce the use of a number line to find rounded numbers. Work through Questions 10–13 with the whole class. Use a number line on the board or other display as students share their responses.

In Question 10, students find a rounded number for 407,997 that is expressed to the nearest hundred thousand. Students are asked to identify benchmarks that they use as they round 407,997. Question 11 asks students to find a rounded number for 458,156 expressed to the nearest hundred thousand. They will once again identify benchmarks. Note that the benchmarks for rounding 458,156 to the nearest 100,000 are the same as those used to round 407,997 to the nearest 100,000. In Question 12, 458,156 is rounded first to the nearest 50,000 (450,000) and then to the nearest 10,000 (460,000). Both of these estimates are acceptable. Discuss which estimate is closer to the actual number. Question 13 provides an opportunity for students to choose benchmarks to estimate.

Question 14 returns to the original question posed in the vignette: Estimate the number of people who visited the planetarium over the two years. In this question, Jerome and Ana both give an estimate based on the convenient numbers that they chose. While Ana's estimate (410,000 + 460,000 = 870,000) is more accurate, the numbers that Jerome used (400,000 + 500,000 = 900,000) are somewhat easier to add using mental math. However, both students have given an acceptable answer. Allow time to discuss when accuracy is desirable and when it is okay to choose numbers that are easier to use. Question 15 provides an opportunity to round numbers to estimate the answer to a subtraction problem.

Questions 14–18 provide additional practice rounding numbers. Have students work with a partner. This will allow them to compare answers and receive immediate feedback on their work. Questions 17D and 18D ask students to determine how accurate one needs to be in two different situations. The context of a problem often dictates the decisions that must be made when estimating. In these cases, it is probably better to overestimate the amount of food and tickets to order—having too few tickets or not enough food causes problems. Ordering too much, however, is a wasted expense. Discuss these issues as you decide on appropriate estimates.

Assign Questions 1–4 in the Homework section. These questions provide independent practice rounding large numbers.