Facts I Know: Multiplication and Division

Est. Class Sessions: 1

Developing the Lesson

Multiplication Facts I Know. Daily Practice and Problems items in this unit will review all the multiplication facts so students can prepare for the Multiplication Facts Inventory Test in DPP item Y in Lesson 8. Use Questions 1–4 in the Student Guide to help students begin this review.

Have students respond to Questions 1–3. In Question 3, students write lists of facts they still need to study, and make new Triangle Flash Cards using the Blank Triangle Flash Cards pages in the Student Activity Book.

Use the following prompts to remind students of appropriate strategies (Question 4).

For example, if a student needs to learn 6 × 9, ask:

How can you remember this fact? Can you use a fact that you already know to help you?
Can you use 6 × 10 to help you find 6 × 9? (Possible response: 6 × 10 = 60, so 6 × 9 is 6 less than 60, or 54)
Can you use doubling to help?

Ask students to use Self-Check: Questions 1–4 in the Student Guide to assess their fluency with the multiplication facts [E12].

Use the following strategies to provide targeted practice:

Support. For students who have many facts that they still need to learn, divide their list into smaller groups of facts for them to study. Choose groups of facts that lend themselves to the use of the same strategy, such as doubling. Assign one group at a time for students to make new flash cards and to study these facts at home. Discuss the strategies that they can use to learn these facts.

Extend. For students who have circled all the facts on their Multiplication Facts I Know charts, ask them to choose one or two facts that were hard for them to learn. Ask them to write the facts on chart paper along with the following: 1) a story and a picture that illustrate the fact; 2) a strategy for learning the fact; and 3) all number sentences in the fact family. Display these charts in the classroom.

Picturing Fact Families. Using the Picturing Fact Families pages in the Student Activity Book, students review fact families through the use of grids (arrays) and rectangles. By this time, most students will be comfortable with fact families and can review this section quickly. Questions 1–3 provide a visual image to help develop understanding and review turn-around facts.

Students cut out the rectangles in Question 3. By rotating one and placing it on the other, they will see that both arrays are the same. All four number sentences (7 × 5 = 35, 5 × 7 = 35, 35 ÷ 7 = 5, 35 ÷ 5 = 7) describe the same rectangle. All are related and belong to the same fact family.

Use the following discussion prompts as needed to review the fact families, terms in the number sentences, and turn-around facts.

Ask:

How are the four number sentences alike? (They all have the same numbers in them. They all represent the same rectangle.)
How are they different? (Two are multiplication sentences and two are division sentences. The multiplication sentences are the same, but the numbers you multiply are switched. The division sentences start with the same number, but the number you divide by and the answer are switched.)
What do you call the two numbers you multiply together? (factors)
What do you call the answer to a multiplication problem? (product)
Name the factors and the product in 5 × 7 = 35. (factors are 5 and 7, product is 35)
What do you call the number you divide by in a division problem? (divisor)
What do you call the number you divide in a division problem? (dividend)
What do you call the answer to a division problem? (quotient)
Name the dividend, divisor, and quotient in 35 ÷ 7 = 5. (35, 7, and 5, respectively)
What do we call a pair of multiplication sentences that have the same product but the factors are in a different order, like these: 5 × 7 = 35 and 7 × 5 = 35? (turn-around facts)
These facts are called turn-around facts because changing the order of the factors does not change the product. Name two other turn-around facts. (Possible response: 3 × 5 = 15 and 5 × 3 = 15)

Turn-around facts and the commutative property. Students learn the multiplication facts more easily because there are turn-around facts in multiplication. For example, 2 × 5 = 10 and 5 × 2 = 10. This is an example of the commutative property of multiplication. The order of the factors does not change the product. Mathematicians say that multiplication is commutative.

Division is not commutative. The order of the dividend and divisor do matter. For example, 10 ÷ 5 = 2, but 5 ÷ 10 = 1/2. The terminology is not as important as the concept. Students can understand this idea with examples such as the following:

If 10 cookies are divided equally among 5 people, how many cookies does each get? Write a number sentence for this story. (10 cookies ÷ 5 people = 2 cookies)
If 5 cookies are divided equally among 10 people, how many cookies does each get? Write a number sentence for this story. (5 cookies ÷ 10 people = 1/2 cookie)
Does the order of the dividend and the divisor matter? (Yes)
Are 10 ÷ 5 = 2 and 5 ÷ 10 = 1/2 turn-around facts? (No)

Practice Division Facts with Triangle Flash Cards. Have student pairs use their Triangle Flash Cards: 5s and their Triangle Flash Cards: 10s to begin assessing their progress with learning the division facts.

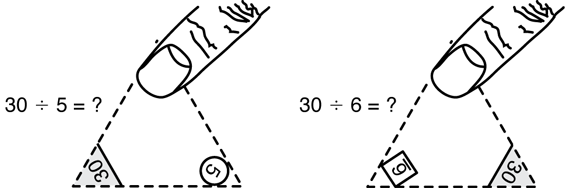
Question 5 in the Student Guide provides a description of how to use the flash cards for division. The procedure is similar to the way the cards were used for multiplication, with one main difference. When using the cards for division, students need to sort the Triangle Flash Cards twice. The first time through the set of cards, partners cover the numbers in squares. The second time through, partners cover the numbers in circles (Questions 5A and 5D). See Figure 1.

After each time through, they make a list of the facts they cannot answer quickly but can figure out using strategies and those they need to learn. Students should use this list to study their facts at home.

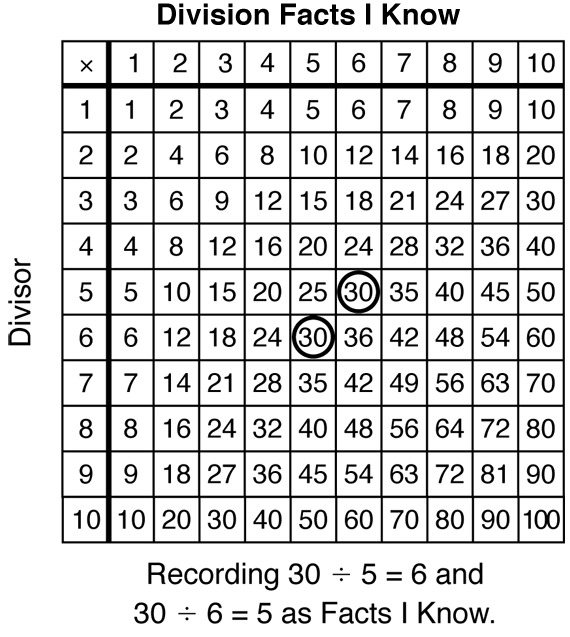
Students also update their Division Facts I Know charts after each time through the entire set of cards (Questions 5C and 5E). See Figure 2. Draw attention to the examples given in Questions 5C and 5D (30 ÷ 5 = 6 and 30 ÷ 6 = 5) and how those division facts are marked in the Division Facts I Know chart.

Demonstrate this sequence using displays of the flash cards and the Division Facts I Know chart.

Remind students that they circle only those facts that were in the pile of facts they know and can answer quickly. They make a list of the facts in the other two piles and take this list home along with their flash cards so they can study the facts with a family member.

Ask students to use Self-Check: Question 5 in the Student Guide to assess their fluency with the division facts for the 5s and 10s [E10].

See the Letter Home for strategies for targeted practice.

Question 6 asks students to compare their Multiplication Facts I Know charts with their Division Facts I Know charts. Because of their work with fact families, students should see many of the same numbers circled on both charts. For example, if a student knows 4 × 5 and 5 × 4, it is very likely he or she will know 20 ÷ 4 and 20 ÷ 5.Thus, two 20s should be circled on the division chart as well (Question 6A). Note that both Facts I Know charts have a multiplication symbol in the first square since both charts are simply multiplication tables used for recording known facts.

Another important difference between the Multiplication Facts I Know chart and the Division Facts I Know chart is that there is no row or column for zero.

Question 6B asks:

Why are there no zeros on the Division Facts I Know chart? (You cannot divide by zero or the 0 cannot be divided.)

Explore Zeros and Division. Use the following discussion prompts to guide a discussion about division and zero. First, review the inverse relationship between multiplication and division using fact families.

Ask:

Write the four sentences in the fact family for 12 ÷ 4. (12 ÷ 4 = 3, 12 ÷ 3 = 4, 3 × 4 = 12, 4 × 3 = 12)

Remind students that there is only one answer to a division problem. Each division problem has a unique solution. For example, there is only one number that makes the following statement true:

12 ÷ 4 = , since 4 × = 12.

Ask:

What number can you put in the boxes to make the above statement true? (3)
For each statement, find one number that makes the statement true.

10 ÷ 5 = , since 5 × = 10 (2)
18 ÷ 3 = , since 3 × = 18 (6)
8 ÷ 1 = , since 1 × = 8 (8)
0 ÷ 2 = , since 2 × = 0 (0)
0 ÷ 3 = , since 3 × = 0 (0)
0 ÷ 10 = , since 10 × = 0 (0)

Find 0 ÷ 9 = . Justify your solution. (0 ÷ 9 = 0, since 9 × 0 = 0)

Use the same reasoning to explore division by zero.

Ask:

Let's try to divide by zero. Find one number that makes the statement true: 2 ÷ 0 = , since 0 × = 2. (No number makes it true.)

Students can see that since zero times any number is zero, there is no number that will make the statement true. We say that division by zero is undefined.

What happens when we try to divide zero by zero?

Find one number that makes the statement true: 0 ÷ 0 = , since 0 × = 0. (Any number works but division has just one correct or unique solution.)

Students may say that 0 × 1 = 0, 0 × 2 = 0, 0 × 3 = 0. In fact, zero times any number is zero. So, there is not just one number that makes the statement true. There is not a unique solution, so we say that 0 ÷ 0 is undefined as well.

The Zeros and Division section in the Student Guide reinforces the concepts explored previously. Students can read and answer Questions 7–12 in pairs or small groups. Note that Question 11 asks students to enter division by zero problems on a calculator. Calculators will display an error message if asked to divide by zero.

Use the problems in Check-In: Question 12 to assess students' abilities to solve division problems involving zero and justify solutions [E8].

The Homework page in the Student Guide provides more practice with division, including problems involving zero. The Mixed-Up Tables pages in the Student Activity Book provide practice with both multiplication and division facts, including multiplying by multiples of 10.