Big Base-Ten Pieces

Est. Class Sessions: 3

Developing the Lesson

Part 1: Partitions of Big Numbers

Divide the class into two groups. Ask each group to choose a spokesperson. Ask one group to choose a small number (e.g., 2452) and the other group to choose a large number (e.g., 230,525) from the Newswire display the class created in Lesson 2.

Create a list of ways to show the different partitions of a number by asking:

What are the ways to show the different partitions of the number your group selected? (Accept all responses: number line, base-ten pieces or shorthand, a number sentence, on a Base-Ten Pieces Recording Sheet, hoppers on a number line.)

Record student responses to create a list of different representations. Within each group, assign pairs of students a different representation to show the number selected by their group. See Figure 1 for a sample list and Figures 2 and 3 for samples of representations. Students can use a Base-Ten Pieces Recording Sheet in their Student Activity Books. After giving them several minutes to work, ask students within each group to share the different representations of their group's number. Start with base-ten pieces or base-ten shorthand.

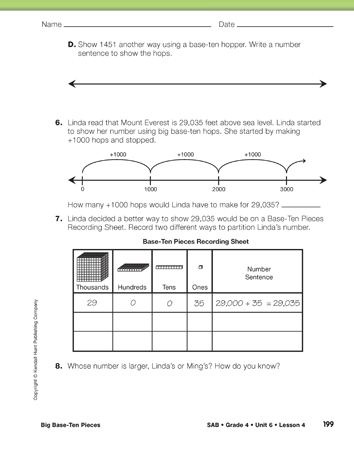
Ask:

What is the largest base-ten block that we have used? (a pack)
What number does it represent? (1000)
How many packs will you have to draw to represent 230,525? (230 packs)
Will that take a long time? How much paper will you need?
Do you think base-ten shorthand is a practical way to show this number? (No, because I need a lot of pieces, and it is time-consuming to draw all those pieces.)

Ask students who showed the partitions of the number using a Base-Ten Pieces Recording Sheet to use a corresponding display to show different partitions of the same number. See Figure 2 for examples. Emphasize that each partition is equal to their number.

Finally, ask students to share how they used the base- ten hopper and a number line to show the partitions of their number.

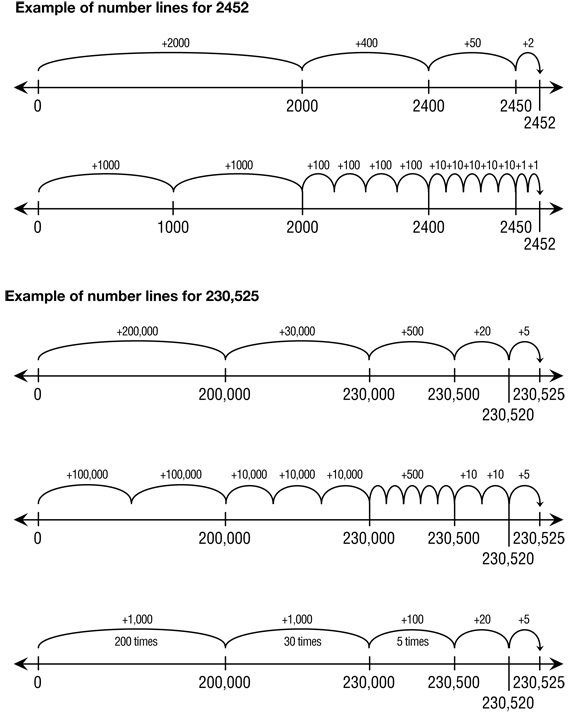
Let groups partition the numbers any way they wish. Remind students that a base-ten hopper can hop by ones, tens, or multiples of ten. Again, students with really large numbers may choose to write the number of a certain size hop rather than drawing all the hops, but let students come to this on their own. See Figure 3 for examples.

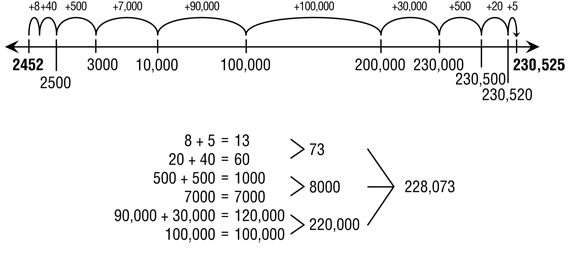
Have each group work together to devise a way to show how far apart the two numbers are from each other. Groups can use number lines or other representations to show the difference. See Figure 4 for a possible strategy.

Repeat the previous discussion by asking one group to choose a different small number and the other group to choose a different large number. Then ask each group to show the partitions of their number using base-ten shorthand, a Base-Ten Pieces Recording Sheet, a number sentence, and base-ten hoppers on a number line.

After sharing and discussing each representation of the numbers, ask and discuss:

How far is the small number chosen by Group 1 from the larger number chosen by Group 2? Show or tell how you know.

Let students explore these representations and number partitions further by assigning Questions 1–8 on the Big Base-Ten Pieces pages in the Student Guide and Questions 1–8 on the Big Numbers pages in the Student Activity Book. These pages can be completed independently or with another student.

Small groups of students can move on to Part 2 with the teacher, while other students work independently on Questions 1–8 on both the Big Base-Ten Pieces pages in the Student Guide and the Big Numbers pages in the Student Activity Book.

Assign problems not completed on the Big Numbers pages in the Student Activity Book for homework.