Decimal Hoppers

Invent Strategies. Begin this part of the lesson by allowing students to invent and explore methods for adding simple decimal numbers. Ask students to work with a partner to add the following numbers using any method they choose:

3.7 + 1.6 = ?

Encourage them to use any of the tools they have been working with in this unit, such as number lines (decimal hoppers), Tenths Helper charts, base-ten pieces, etc. Ask several students to show and explain their solutions, encouraging a range of methods to be shared.

Have students find the following sums and differences using any method they choose.

3.3 − 1.2 = ?
1.25 + 2.55 = ?
3.75 − 2.1 = ?

Ask several students to explain their solutions and strategies to the class.

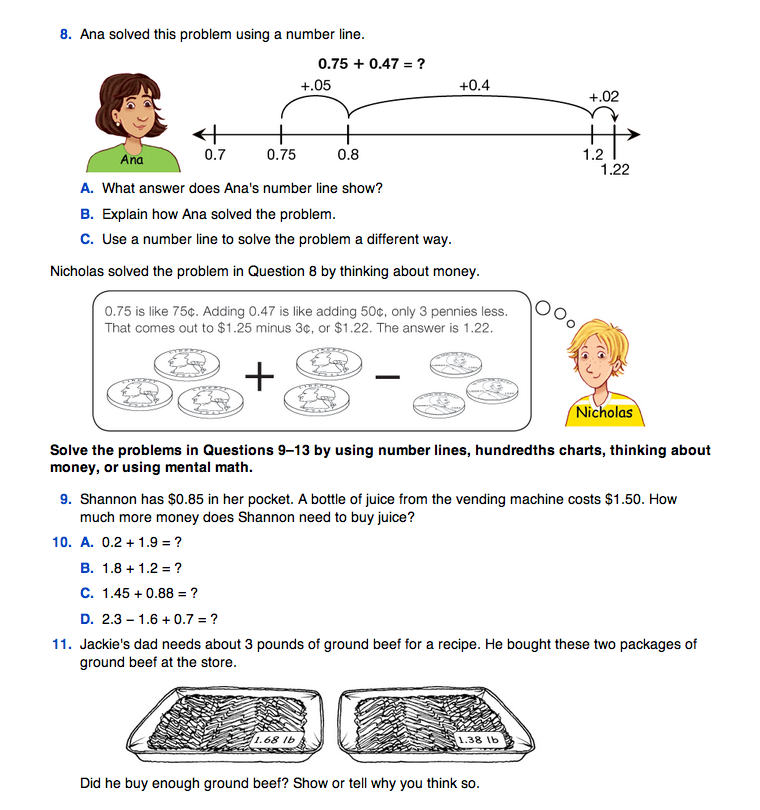
Add and Subtract with Models. Read and discuss Questions 6, 7, and 8 in the Adding and Subtracting with Decimals section of the Student Guide. These questions show models students might use to add and subtract decimal numbers. One of these models is an open number line, which allows students to perform operations as left and right movements. Remind students that when using the number line in this way, they are “freed from the rules” of the decimal hopper. In other words, students can “hop” any distance along the number line that makes sense to them for solving a problem. They are not limited to hops of 1, 0.1, 0.01, etc., like the decimal hoppers were.

As an example, in Question 8, Ana finds the sum 0.75 + 0.47 by starting on the number line at 0.75, then moving 0.05 to the right to get to 0.8, then moving 0.4 to the right to get to 1.2. So far, she has added a total of 0.45 to 0.75. Since the sum requires adding 0.47 to 0.75, she moves 0.02 further to the right to get to 1.22.

Along with the number line, thinking about money is another conceptual model demonstrated by Nicholas in Question 8. Since money is a familiar context that is represented by decimal numbers, it is a useful tool for adding and subtracting decimal numbers mentally. Encourage students to use a range of conceptual representations to find sums and differences with decimals before introducing more formal numerical algorithms. Each representation solidifies and deepens students' conceptual foundations about operations with decimal numbers, and will help them bring number sense into increasingly complex computations in the future.