Using Decimals
Fraction quantities can be represented numerically using either common fractions or decimal fractions. … read more
Fraction quantities can be represented numerically using either common fractions or decimal fractions. Students are familiar with common fractions, expressed with a numerator and denominator as with 1/2, 3/5, 7/10, 25/8, or 9/4. Decimal fractions, or decimals, express fractional quantities by including digits to the right of a decimal point, as with 0.5, 0.046, or 2.33. Decimals make use of base-ten place-value concepts to symbolize fractional quantities, which makes them particularly useful for performing computations and recording measurements.
The MEANING of DECIMALS

Students make sense of decimal fractions by connecting decimal concepts to their existing understanding of … read more
Students make sense of decimal fractions by connecting decimal concepts to their existing understanding of common fractions and by exploring various representations of decimal fractions. For example, students learn the meaning of decimals by reading “4.3” aloud as “four and three-tenths,” writing 1.36 as 1 + 3/10 + 6/100, or seeing that 1/2 of a meter and 0.5 meter occupy the same location on a meterstick. As important, students extend their knowledge of whole number place value to decimals. In the base-ten system, each digit place represents a multiplier ten times that of the next place to the right. For example, the tens place has a value of 10 times the ones place. The hundreds place has a value of 10 × 10, or 100 times the ones place. Applying place value concepts to the right of the decimal, the tenths place has a value of 1/10 the ones place, and the hundredths place has a value of 1/100 of the ones place.
REPRESENTATIONS and MODELS

Representations
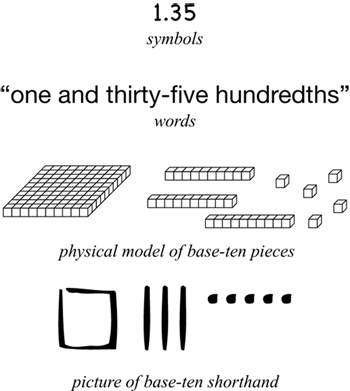
In this unit, students make connections among different representations of decimals: symbols, words, physical … read more
Representations
In this unit, students make connections among different representations of decimals: symbols, words, physical models, and pictures. See Figure 1. Translating among these representations—drawing a shorthand picture of a collection of decimal base-ten pieces, saying numerical decimal fractions aloud, and writing a decimal number—helps students maneuver between the many contexts in which decimals appear in the real world and helps develop conceptual understanding of decimal fractions. Research indicates that students with a foundational understanding of decimals can learn computational procedures and solve problems involving decimals more effectively (Ball, 1993; Hiebert & Wearne, 1986; Hiebert, Wearne, & Taber, 1991; Lesh, Post, & Behr, 1987; National Research Council, 2001).
The Area Model
Research indicates that the area model provides a powerful context for students' early work with … read more
The Area Model
Research indicates that the area model provides a powerful context for students' early work with fractions and decimals (Behr & Post, 1992; Cramer, Post, and delMas, 2002). In particular, the use of fraction circle pieces and rectangles helps students establish ideas about equal parts, relative sizes of fractions, equivalent fractions, unit wholes, and operations on fractions. Children build on their everyday experiences (cutting toast, sharing pizza, etc.) when they use such models. Many real-life measurement situations (cooking, sewing, carpentry) involve fractions that are similar to fractions modeled with rectangles or circles. In this unit, area models are adapted specifically for decimal fractions. Fraction circle pieces representing fifths and tenths are used to build number sense of decimals to the tenths place. Tenths Helper charts and Hundredths Charts allow students to model decimals using rectangles.
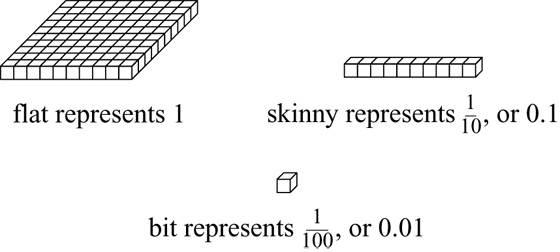
Students also use base-ten pieces to model decimals to the hundredths place, but with an important change. When modeling whole numbers with base-ten pieces, the unit whole is represented as a bit. When modeling decimals, however, the unit whole is represented by a flat. Consequently, a skinny now represents 1/10 (0.1) and a bit 1/100 (0.01). See Figure 2. Students have completed many activities in which the size of the whole changes, including lengths on a number line and sizes of pizza slices, so this change is a natural extension of their understanding that the size of the whole changes in varied contexts. Using base-ten pieces in this way provides a connection point to existing understandings about place value with whole numbers. (Strictly speaking, base-ten pieces are a volume model for decimals and not an area model, but they can be interpreted as an area model when drawn on paper or viewed from above.)
The Number Line
When a decimal fraction is represented on a number line, it is understood to occupy a unique location along a … read more
The Number Line
When a decimal fraction is represented on a number line, it is understood to occupy a unique location along a continuous scale. Students' familiarity with ruler measurement, number lines, and base-ten hoppers makes this a useful model for understanding decimals. In this unit, students represent decimals on number lines by measuring lengths to tenths of a meter and hundredths of a meter in a lab context. Students also locate decimal fractions on scaled number lines and move “decimal hoppers” between number line locations. These activities establish number sense about how moving 1 unit along a number line compares with moving 0.1 units or 0.01 units.
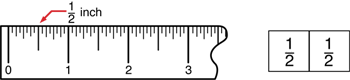
Students may have misconceptions about fractions on number lines because the focus shifts from an amount of area to a position on a number line. For example, in trying to locate 1/2 inch on a ruler, a child might become confused by thinking about 1/2 of the whole ruler. Furthermore, on a ruler or number line, the position is marked at the endpoint of the length. This is a departure from the area model, where labels are typically shown in the center to represent the entire quantity of area. See Figure 3. These differences may present some difficulty at first, but will deepen understanding as students grow accustomed to the features of each model.
Money
Money is a useful model for representing and operating on decimals for two reasons. First, money is … read more
Money
Money is a useful model for representing and operating on decimals for two reasons. First, money is commonly shown with decimals to the hundredths. Second, children typically have good intuition for situations involving money. Certain conventions in our way of writing money, however, make its use problematic for beginning instruction in decimals. For example, we usually write amounts of money using exactly two decimal places (e.g., $4.50, not $4.5). Pure decimal numbers do not have this constraint; 4.50 is as correct as 4.5. One can also think of an amount like $4.58 in terms of two distinct units, dollars and cents. In this interpretation, the number before the decimal point tells how many dollars, and the number after the decimal point tells how many cents, thus making it harder for students to see $.58 as a decimal fraction of a dollar and not simply as “58 cents.” It may be useful, therefore, to encourage students to interchange the terms “cents” and “hundredths of a dollar” to create a more general representation of decimals when modeling with money.
OPERATIONS WITH DECIMALS

In this phase of learning about decimals, students are still developing a foundational understanding of … read more
In this phase of learning about decimals, students are still developing a foundational understanding of decimal concepts. The work in this unit—skip counting, measuring, comparing to benchmarks, ordering, translating between various representations—is designed to support this conceptual development. Formal algorithms for paper-and-pencil addition and subtraction are not introduced until fifth grade because premature attention to formalized computation at this stage can pre-empt students' initial sense-making about decimals. For most students in fourth grade, it is more profitable to think through a few problems involving decimal computation rather than spending considerable time learning computational procedures.
In this unit, students invent their own methods to solve problems involving the addition and subtraction of decimals. They are also introduced to several informal models that support sense-making with decimal computations, including number lines, decimal hoppers, tenths helper charts, hundredths charts, and money. Establishing students' conceptual understanding before learning formal procedures for decimal computations is consistent with the way students learned whole-number arithmetic.
METRIC UNITS

The names of the metric units are logically constructed. There are three fundamental metric units: … read more
The names of the metric units are logically constructed. There are three fundamental metric units: the meter (length), the gram (mass), and the second (time). The liter and many other units are defined in terms of these three. By combining these basic units with various prefixes, many convenient units of measure are obtained.
The prefixes come either from Latin or Greek. The Greek prefixes are used to indicate multiples of the basic unit; the Latin prefixes indicate subdivisions of the basic unit. For example, the Greek kilo- (1000) yields kilogram and kilometer, meaning 1000 grams and 1000 meters, respectively; the Latin milli- (1000) yields millimeter and milligram, meaning 1/1000 meter and 1/1000 gram.
Here are some of the most common metric prefixes and their meanings:
- micro- (1/1,000,000)
- mega- (1,000,000)
- milli- (1/1000)
- kilo- (1000)
- centi- (1/100)
- hecto- (100)
- deci- (1/10)
- deka- (10)
MATH FACTS and MENTAL MATH

This unit continues the review and assessment of the division facts to develop mental math strategies, … read more
This unit continues the review and assessment of the division facts to develop mental math strategies, gain proficiency and to learn to apply multiplication strategies to larger numbers. Students will focus on the division facts related to the last six multiplication facts (24 ÷ 4, 24 ÷ 6, 28 ÷ 4, 28 ÷ 7, 32 ÷ 4, 32 ÷ 8, 42 ÷ 6, 42 ÷ 7, 48 ÷ 6, 48 ÷ 8, 56 ÷ 7, 56 ÷ 8).
Resources
- Ball, D.L. “Halves, Pieces, and Twoths: Constructing Representational Contexts in Teaching Fractions.” In Rational Numbers: An Integration of Research. T.P. Carpenter, E. Fennema, and T.A. Romberg, eds., Lawrence Erlbaum Associates, Hillsdale, NJ, 1993.
- Behr, M. and T. Post. “Teaching rational number and decimal concepts.” In Teaching Mathematics in Grades K–8: Research-Based Methods, 2nd ed. T. Post, ed. Allyn and Bacon, Boston, 1992.
- Cramer, K., T. Post, and R. delMas. “Initial Fraction Learning by Fourth- and Fifth-Grade Students: A Comparison of the Effects of Using Commercial Curricula with the Effects of Using the Rational Number Project Curriculum.” Journal for Research in Mathematics Education, 33 (2), pp. 111–144, March 2002.
- Hiebert, J., and D. Wearne. “Procedures over Concepts: The Acquisition of Decimal Number Knowledge.” In Conceptual and Procedural Knowledge: The Case of Mathematics. J. Hiebert, ed. Lawrence Erlbaum Associates, Hillsdale, NJ, 1986.
- Hiebert, J., D. Wearne, and S. Taber. “Fourth Graders' Gradual Construction of Decimal Fractions during Instruction Using Different Physical Representations.” Elementary School Journal, 91 (4), pp. 321–341, 1991.
- Lesh, R., T. Post, and M. Behr. “Representations and Translations among Representation in Mathematics Learning and Problem Solving.” In Problems of Representation in the Teaching and Learning of Mathematics (Chapter 4), C. Janvier, ed. Lawrence Erlbaum Associates, Hillsdale, NJ, and London, 1987.
- National Research Council. “Developing Proficiency with Other Numbers.” In Adding It Up: Helping Children Learn Mathematics. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001.
- Wearne, D., and J. Hiebert. “Cognitive Changes during Conceptually Based Instruction on Decimal Fractions.” Journal of Educational Psychology, 81 (4), pp. 507–513, 1989.











