Tangrams

Est. Class Sessions: 2–3

Developing the Lesson

Part 1. Exploring the Tangram Pieces

Some students may have more difficulty than others with this unit. It involves spatial sense—a student's awareness and understanding of shapes and the relationship between shapes. Although some students may show better understanding of spatial sense than others, people are not born with or without spatial sense—it can be developed. Consistent and meaningful hands-on exploration with shapes and discussion of the relationships between them will develop spatial sense and build geometric understanding over time.

Sort Tans. Begin the lesson by reading the Tangrams page in the Student Guide. The page introduces tangrams as old Chinese puzzles containing seven pieces called tans. If you have gathered resources that show tangram designs, share them with the students.

Distribute a set of 7 tangram pieces to each student. Assign Question 1 to give students the opportunity to explore the pieces and to try to make a tangram design. The designs do not need to be elaborate. This is simply a way to introduce the pieces.

In Question 2, students are asked to sort the 7 tangram pieces in any way they choose. Allow them to explore and find shared traits without directing them to formalized categories. After they have had time to sort the tangram pieces, ask them to record their groupings on the Tangram Sort page in the Student Activity Book. Students should trace each piece and show which ones are grouped together by circling them or by drawing lines to partition them into groups.

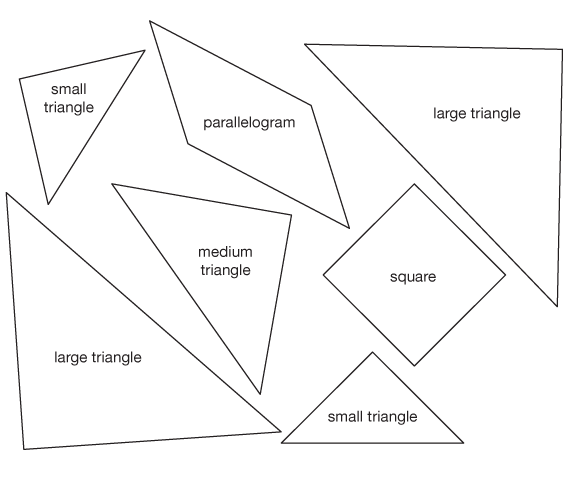
Use Tangram Sort in the Student Activity Book to assess students' progress toward describing and analyzing two-dimensional shapes using their properties [E1].

Agree on Shape Names. Two purposes of this part of the lesson are to highlight the characteristics of the shapes and to learn their names. Display the Tangrams page in the Student Guide. Agree on the names for the seven tans and reinforce the shape names in this discussion. In this unit, the following names are used: small triangle (2 pieces), medium triangle (1 piece), large triangle (2 pieces), square (1 piece), parallelogram (1 piece). See Figure 2.

Share Sorts. Once this is accomplished, ask for volunteers to display their Tangram Sort page and relate how and why they sorted their shapes. Some possible sorts are:

size: small, medium, and large.
number of sides: three or four sides.
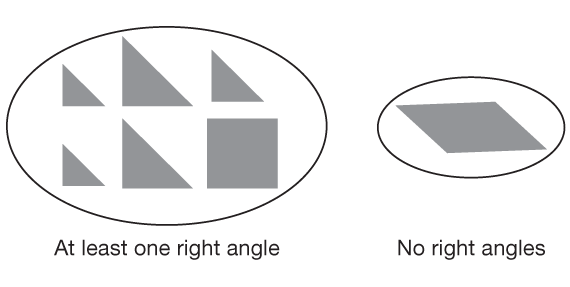
right angles: right angles (square angles) in shape or no right angles. (The tangram parallelogram has no right angles.) See Figure 3.
pairs: the shape is part of a pair or is not part of a pair. (The large triangles and the small triangles are congruent to each other, and therefore form a pair. The other tangrams are singles and are not part of a pair.)
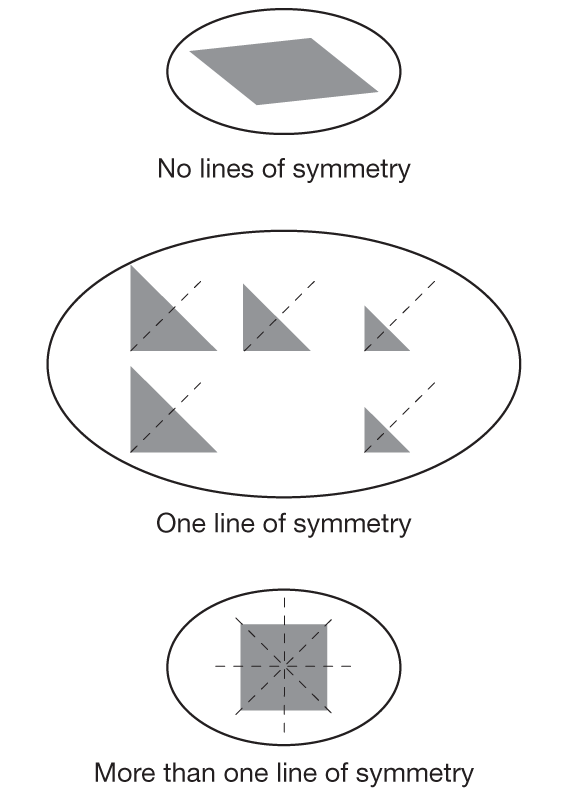
lines of symmetry: the shape has no line of symmetry, one line of symmetry, or more than one line of symmetry. (The parallelogram has no lines of symmetry, the triangles have one line of symmetry, and the square has four lines of symmetry.) See Figure 4.

Guess the Rule. There are many possible sorts. After two or three students report on their sorts, ask another student to show his or her sort on a display without revealing the rule for how the tangrams were sorted.

Ask the class to guess the rule for the sort. As this is being done, ask questions such as:

Pick one of the groups in the sort. What do the shapes in this group have in common?
Choose one of the shapes in this group. Why does it belong in this group?
Choose a shape that is not in this group. Why doesn't it belong to this group?

Using informal language to describe the geometric terms in this unit is appropriate at this level of study. For example, students may say a shape has “square angles” instead of right angles. You may use terms such as congruent and symmetry in your discussion as a way of introduction, but it is not expected that students become fluent with this language at this time.

Use a display a set of tangram pieces.

Pick two shapes to compare, the square and parallelogram for example, and ask:

How are these two shapes alike? (Possible response for square and parallelogram: They both have four sides, straight sides, and four corners. Both the square and the parallelogram have opposite sides that are always the same distance apart, or parallel.)
How are these two shapes different? (Possible response for square and parallelogram: The square's corners are square, but the parallelogram's corners are not. All of the square's sides are the same length. The parallelogram has 2 pairs of opposite sides that match in length. I can fold the square in half and both halves will be the same, but that is not the case with the parallelogram.)

Pick two other shapes to display and compare the similarities and differences between them.

Next, display the whole set of tangrams and ask:

What do all of the shapes in the tangram set have in common? (Possible response: They all have straight sides; they all have corners.)

Assign the Homework section of the Student Guide. Students will continue to practice describing and analyzing two-dimensional shapes using their properties.

Student Guide: 303

Answers