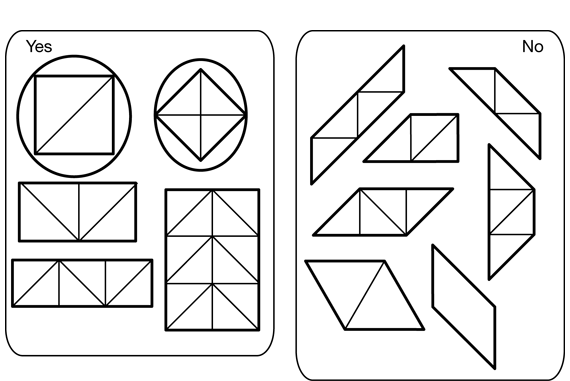
Continue to play Mystery Sort but tell students you are going to sort the shapes by shape categories: rectangles, parallelograms, rhombuses, trapezoids. Place all the rectangles in the “Yes” column and non-rectangles in the “No” column. See Figure 6.
- What is the same about all of the shapes in the “Yes” column? (The opposite sides are parallel, all right angles, and opposite sides are the same length.)
- What are these shapes called? (rectangles)
- Are there any squares in the “Yes” column? (Yes, there are two.)
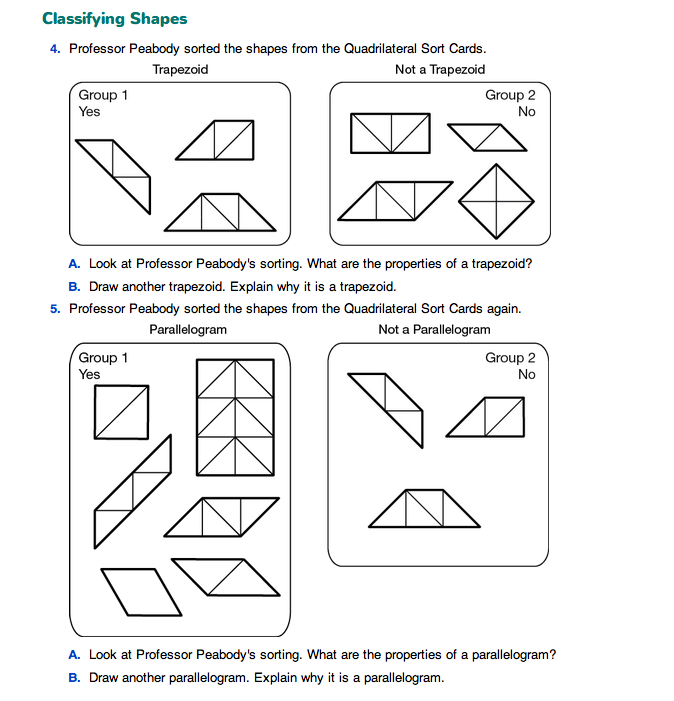
- Why are there squares with the rectangles? (Squares are special kinds of rectangles but they are still rectangles.)
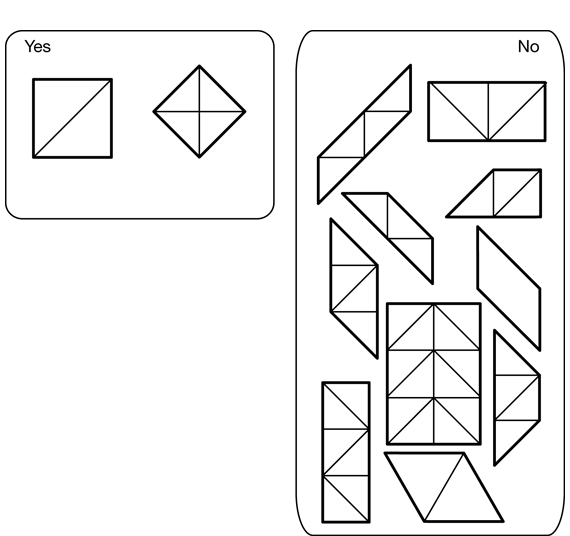
Play Mystery Sort by placing all the squares in the “Yes” column and non-squares in the “No” column. See Figure 7.
- What is the same about all the shapes in the “Yes” column? (The opposite sides are parallel, all right angles, opposite sides are the same length, and all sides are the same length.)
- What are these shapes called? (squares)
- Can I move a rectangle to the “Yes” column? (No, not all rectangles have sides all the same length.)
- Why do the rectangles not fit with the squares? (Some rectangles have different length sides; therefore, they are not squares.)
- Can shapes be called by more than one name? (Possible response: Yes, for example, squares are also rectangles and rectangles are quadrilaterals.)

Is a Square Also a Rectangle? The geometric reasoning that is necessary to answer this question is not trivial for many third-graders. To be able to classify a square as a rectangle, students must be able to reason about the relationships between the shapes. For example, they may think, “A rectangle is a quadrilateral with four right angles, and opposite sides are parallel. A square has all those properties, so it must be a rectangle, too.” This reasoning is at Level 2 in the Van Hiele Levels of Geometric Thought (described in Mathematics in this Unit section). Such thinking depends on successful experiences of visualizing of shapes at Level 0 and analysis of shapes by their properties at Level 1. Geometric reasoning at Level 2 allows students to classify shapes into hierarchies: squares are rectangles, rectangles are parallelograms, parallelograms are quadrilaterals, and quadrilaterals are polygons. The activities in previous grades and in this unit in which students identified and analyzed shapes by their properties prepare students for this level of thought.
Students will focus on classifying shapes into hierarchies in Grade 4. Focus on developing students' abilities to describe and analyze a group of shapes rather than just a single shape.
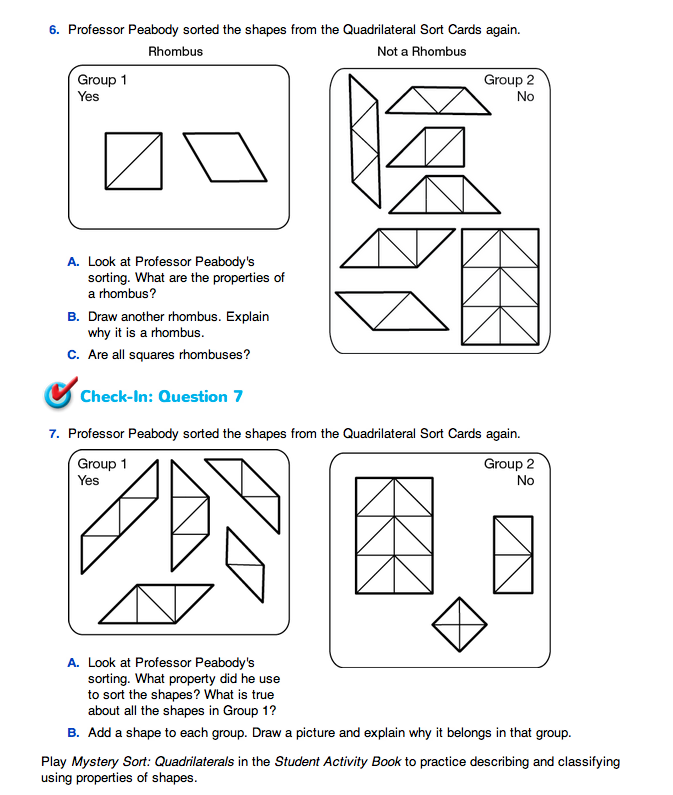
Ask students to continue analyzing shapes by assigning Questions 4–7 in the Student Guide.
Use Check-In: Question 7 in the Student Guide to assess students' abilities to describe and analyze two-dimensional shapes [E1]; identify and draw two-dimensional shapes [E3]; classify shapes [E4]; and justify conclusions using properties [E7].
Organize students to play Mystery Sort using the starred category cards. This will reinforce the terms introduced in Questions 4–7: rhombus, parallelogram, rectangle, and trapezoid.

Definitions. In this unit, students are not developing rigorous definitions for shapes but rather noticing similarities in properties and that shapes can be grouped by different properties. Students have probably developed a definition or at least an image of a square, rectangle, and trapezoid based on previous experiences. Sorting activities help students make connections between the properties of shapes.
Trapezoid. Math Trailblazers uses the definition of trapezoid that states that a quadrilateral is a trapezoid if it has exactly one pair of parallel sides. Using this definition, parallelograms are not trapezoids because they have two pairs of parallel sides. Other mathematicians use another common definition that says a quadrilateral is a trapezoid if it has at least one pair of parallel sides. This definition includes parallelograms.