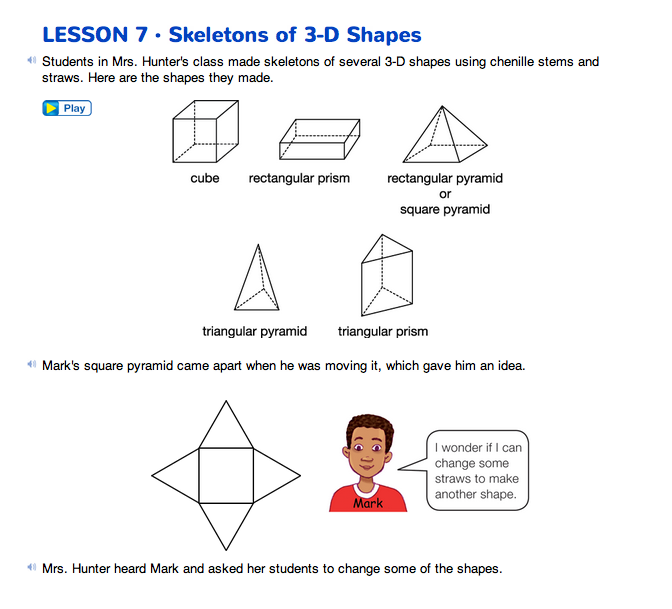
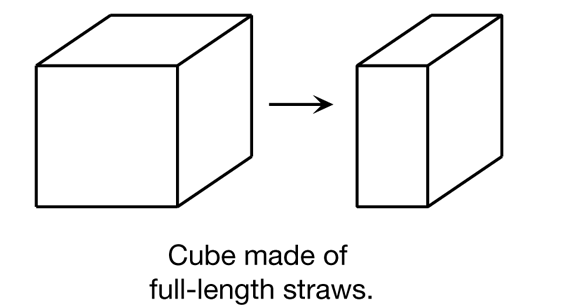
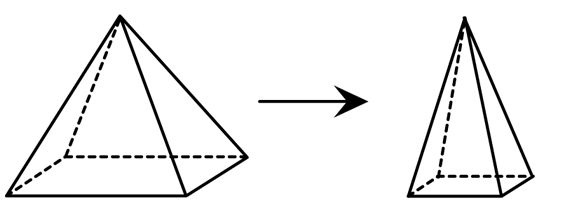
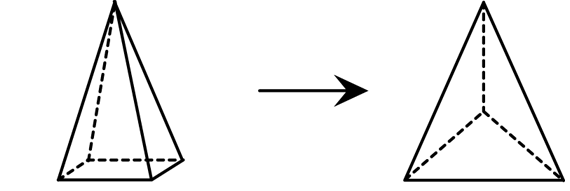
Skeletons of 3-D Shapes

Est. Class Sessions: 2

Developing the Lesson

Part 2. Manipulating Shapes

Manipulate 3-D Skeletons. Read together the vignette on the Skeletons of 3-D Shapes pages in the Student Guide. Distribute half-length straws to student pairs. Then read aloud Questions 1–5, stopping to ask students to make a prediction before they modify the shapes as described in each problem. For example, before completing Question 1 students should predict which straws need to be changed to make the new shape and how the number of vertices, shape of faces, and number of edges will change or which will stay the same. See the TIMS Tip.

Having students make predictions for each problem prior to trying out the solution will facilitate visualizing the relationship between shapes. Visualization is one aspect of helping students develop geometric thinking. You can tally predictions from each student pair as a whole class or have each pair jot down their predictions on a piece of paper.

Have students confirm their predictions by modifying their models as described in the problem. Students should also analyze the new shape to compare the properties of the new shape to those of the original shape. Students should analyze the number of edges, parallel edges, vertices, and right angles. See Figures 3–5 for solutions to Questions 1–3.

Display a cube and two different rectangular prisms that are not cubes from the Power Solids® or class collection of 3-D shapes.

Ask:

What is the same about all of these shapes? (the number of vertices [corners], the number of edges, and the number of faces)
What is different about these shapes? (the shapes of the faces, some have two squares and four rectangles, some have all rectangles, some have all squares)

Display several different kinds of prisms from the Power Solids® or class collection of 3-D shapes (e.g., triangular prism, square prism, hexagonal prism).

Ask:

What is the same about all these shapes? (two faces that are the same and parallel to each other)
What is different about these shapes? (the shapes are different, the number of vertices are different because the base shapes are different, the number of edges are different because the base shapes are different)

Display the square pyramid and the triangular pyramid.

Ask:

What is the same about these shapes? (Both shapes have triangle-shaped faces.)
What is different about these shapes? (Each shape has a different base shape. One has a triangle as a base and the other has a square as a base.)
Which shape is the square pyramid? [Show square pyramid shape.] Why do you think it is called that? (Because the base of the shape is square.)