To give students more experience with tangrams, ask them to make squares with one, two, three, four, and then seven tangram pieces. Students trace their solutions on paper. See Meeting Individual Needs.
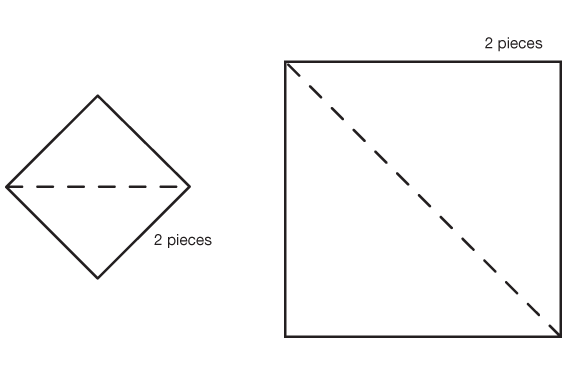
- How can you use two tans to make a square? (There are two solutions: one built from two small triangles and one from two large triangles. See Figure 7.)
- What is true about the two tangram pieces that you used? (The triangles used are the same size and shape, or congruent. There are two sets of congruent triangles in a set of tangrams: one set of large triangles and one set of small triangles.)
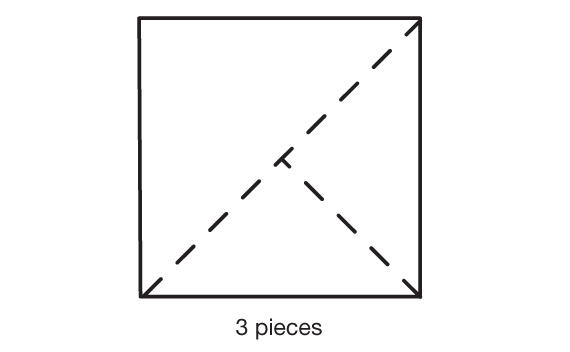
- How can you use three tans to make a square? (1 medium triangle and 2 small triangles; See Figure 8.)
- What is the area of the square made with three tans? How do you know? (4 square inches; I used the Area of Tangram Pieces chart to find that the area of the medium triangle is 2 square inches and each small triangle's area is 1 square inch. The area of the 3-piece square is 2 square inches + 1 square inch + 1 square inch = 4 square inches.)
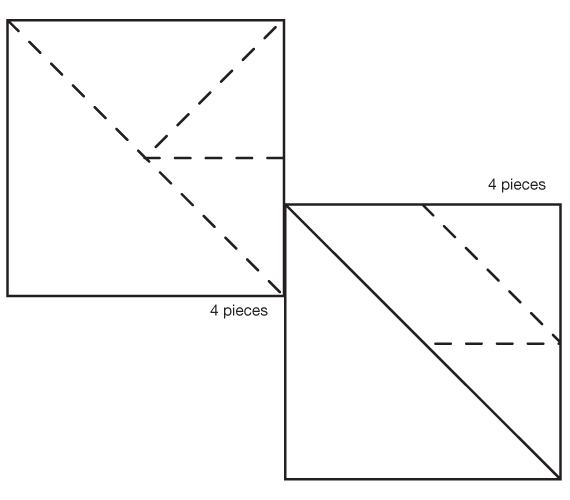
- How can you use four tans to make a square? (See Figure 9 for two solutions.)
- What is the area of each of these squares? How do you know? (8 square inches; responses will vary depending on the pieces used. Possible response: 2 small triangles, 1 large triangle, and 1 parallelogram make this square. I started with the small triangle piece. I know the area of each small triangle is 1 square inch. I know the area of the large triangle is 4 small triangles or 4 square inches. The area of the parallelogram is like 2 small triangles, 2 square inches. 1 square inch + 1 square inch + 4 square inches + 2 square inches is 8 square inches, the area of this square.)
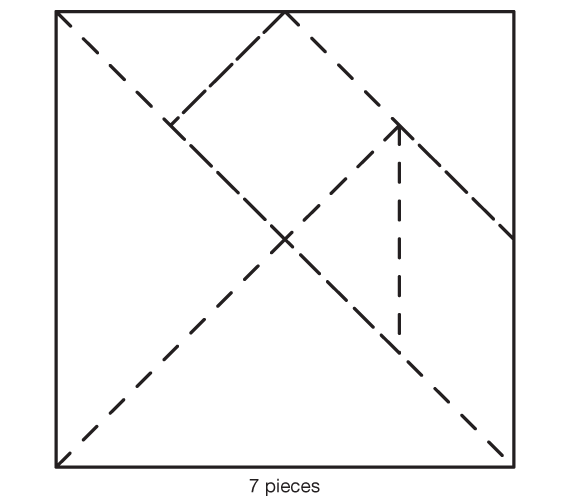
- How can you use all seven pieces to make a square? (There is one solution. The square can be rotated and flipped into eight different configurations. See Figure 10.)

- These are challenging puzzles. Some students will be able to draw some of the squares shown in Figures 7–10. It is not expected that students find all these ways of making squares. However, the more practice students have in trying to construct these squares, the more comfortable they will become filling in the Tangram Puzzles throughout the unit. Use the optional Using Tans to Make Squares Master with shape outlines as needed.
- Some students may require clues to help them create a square. One clue is to put pieces together to make right angles or put pieces together to make triangles that can then be put together as a square.
Give students some time to try to make a square with all 7 tangram pieces. This may be difficult for some students. After students have had some time to work on the solution, distribute copies of the Find the Area Assessment Master. If students were previously unable to make the square with all 7 pieces, they can place their pieces on the Master to make one. Assign Questions 1–2. Students are asked to find the area of the 7-piece square and another shape.
Assign Make and Measure in the Student Activity Book as homework.
Use the Find the Area Assessment Master with Feedback Box to assess students' abilities to measure the area of two- dimensional shapes [E10]; and to find a strategy [MPE2]; show work [MPE5]; and use labels [MPE6].