Tangrams

Est. Class Sessions: 2–3

Developing the Lesson

Part 2. Area of the Tans

Find the Area. Display and refer students to the Area of Tans page in the Student Activity Book. The students will use the square-inch grid on the page to find the area of each of the tangram pieces.

Ask:

What does each square on the grid represent? (1 square inch)
What does each small triangle within a square on the grid represent? ( 1/2 square inch)
What is the area of the square tangram piece? Show how to measure it. (2 square inches)

Notice that the square is placed so the diagonals of the square are grid lines. In this way, we can see that the square is divided into four congruent triangles, where each triangle covers half of a one-inch square. Adding up the four half-square inches we find that the square has an area of 2 square inches.

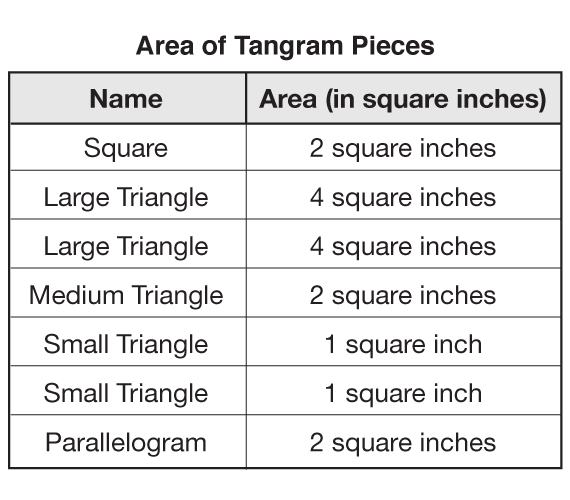
Assign Question 1 and ask students to find the area of the other tans. When all the students have completed the task, collect area information for each of the tangram pieces. Complete the Area of Tangram Pieces chart you prepared as the students share their information. (See Materials Preparation. See Figure 5 for a completed chart.) If there are discrepancies, students can show their work on a display and discuss where an error was made.

When displaying the Area of Tans page, use a square-inch tile to better illustrate the area each square on the grid covers.

Display the Area of Tangram Pieces chart throughout the unit for students to have as a reference.

Verify the Area. Challenge students to verify the area of each shape another way by exploring the relationships between the pieces.

Ask:

How could you find the area of the pieces without grid paper? (Suggestions will vary.)
Explain how you could use smaller shapes to find the area of larger shapes. (Possible response: I could see how many smaller shapes cover the larger shape.)
What is the area of the small triangle tangram piece? (1 square inch)
How can you use that information to find the area of other pieces? Give an example. (Possible response: The parallelogram can be covered by 2 small triangles, so its area is 2 square inches.)
Use the small triangle to check your measurement of the square. (2 small triangles fit onto the square. 1 square inch + 1 square inch = 2 square inches. The area of the square is 2 square inches.)
Does it match your first measurement?

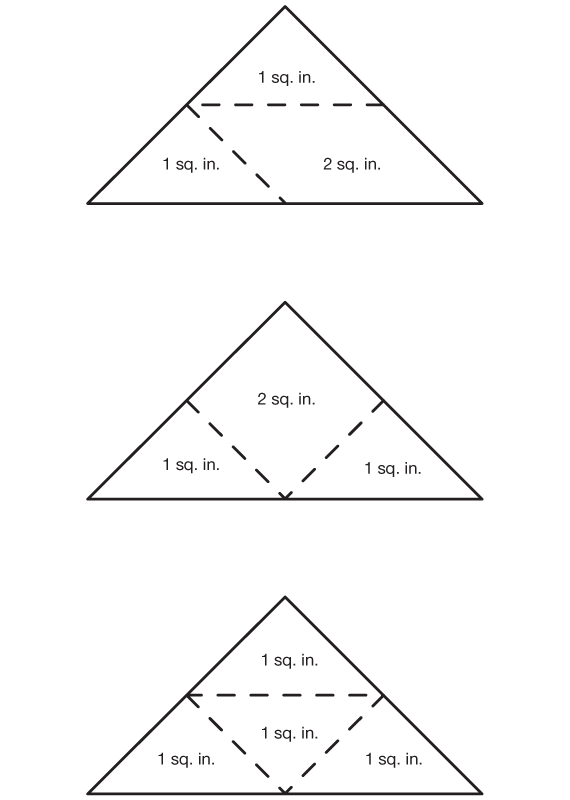
Continue asking the same questions about the medium triangle and the large triangle so that students can verify their measurements.

Ask:

How many small triangles cover the large triangle? (4)
If the area of the small triangle is 1 square inch, what is the area of the large triangle? (4 square inches)
Are there other combinations of tangram pieces that can cover the large triangle?

Direct students to the Large Triangles section of the Area of Tans page in the Student Activity Book. Assign Question 2. Students will find shape combinations that cover the large triangle, trace the shapes onto the outlines, and label the areas in order to verify the triangle's area of 4 square inches. Examples are given in Figure 6. When students are ready, ask them to share the shape combinations and to show how they verified the area.

Student Guide:

Student Activity Book: 421 422

Answers