Lesson 4

Building with Triangles

Est. Class Sessions: 2

Summarizing the Lesson

After students have built shapes with two and three triangles and recorded the results in their tables, you can summarize the main ideas as you work together to make a class table of shapes that can be made with four triangles.

Draw a table on chart paper that is similar to the tables completed for two and three triangles. Ask students to build a shape with four triangles and to fill in rows of the table. Have students draw a sketch or trace the display of the small right triangles. Ask them to discuss the properties of their shapes. For each shape, ask how they know it is different from those that have already been entered in the table.

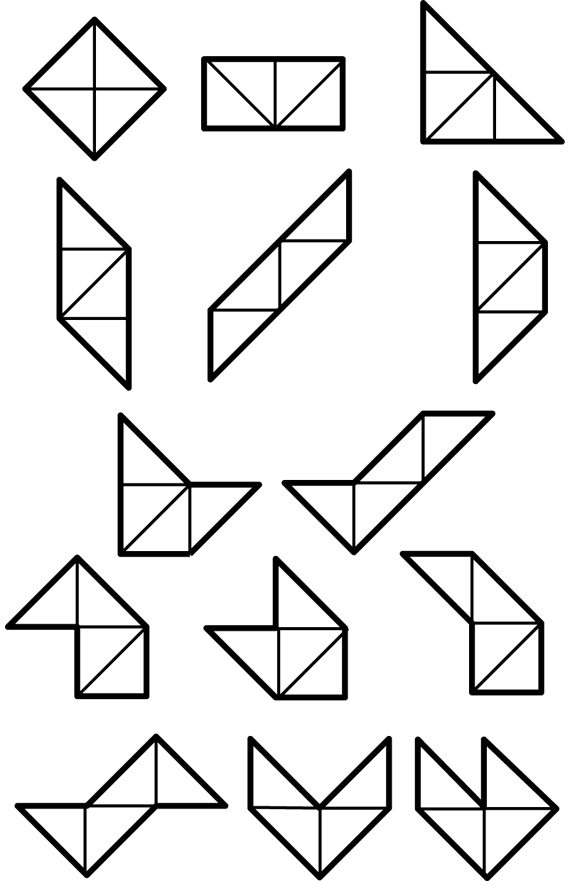
There are fourteen different shapes that can be made with four triangles. See Figure 9. It is not necessary that the class finds them all, but you can challenge interested students to see how many they can find. See the Content Note about Proof for more about asking students to justify their reasoning.

Assign the Investigating Shapes Assessment Master as a baseline assessment to determine if students grasp concepts of shape properties, congruency, and symmetry.

X

Use the Investigating Shapes Assessment Master to assess students' abilities to describe and analyze the properties of two-dimensional shapes [E1]; identify congruency [E5]; and identify lines of symmetry [E6].

X

Proof. In his wonderful book How to Solve It: A New Aspect of Mathematical Method, George Polya distinguished between problems to find and problems to prove. Most problems children encounter are problems that require an answer to be found, usually through computation; these are “problems to find.” Making a mathematical argument—like showing that no shapes can be made with four triangles other than those in Figure 9—is a “problem to prove.” You may find the arguments your students give are inadequate at first, but they will improve with practice. Spend some extra time discussing your students' arguments in order to clarify what makes them compelling or not.

Student Guide:
Student Activity Book:
Master:
Fourteen ways of putting four isosceles right triangles together edge to edge
X
+