Testing Congruence. There are three ways to test if two shapes are congruent:
- slide a shape from one place to another (when you slide a shape, it doesn't change the size or shape) B B
- flip a shape (across a line—now making the shape facing in the opposite direction, like looking in a mirror) B B
- turn a shape (it rotates), e.g., 90 degree turn B B
When working with the triangles in this activity, students are likely to make the following parallelograms.
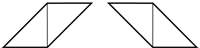
To show these are congruent you must use a flip.
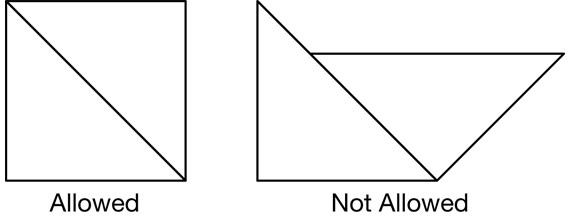
Edge-to-Edge Rule. In this section, students will make all possible shapes using two right triangles. Refer students to Question 5 on the Building with Triangles pages in the Student Guide. Students revisit congruence and review the rules for building with triangles. The first rule is the edge-to-edge rule. Shapes must be built with only edges (sides) of the same length touching and with those edges meeting along their entire length. Shapes with triangles that overlap or touch only at one point are not used in this activity. See Figure 3. This rule limits the number of figures that can be made and facilitates record keeping.
Same-Shape Rule. The second rule is the same-shape rule: turns and flips of a given shape (congruent figures) are considered to be the same shape. See the Content Note about Same and Different: Flips, Turns, and Congruence.
As students find shapes they can make with two right triangles, you might ask them to trace them onto a display using the display of four small triangles from the Right Triangle Master. This will help students decide if a shape is being shown again.
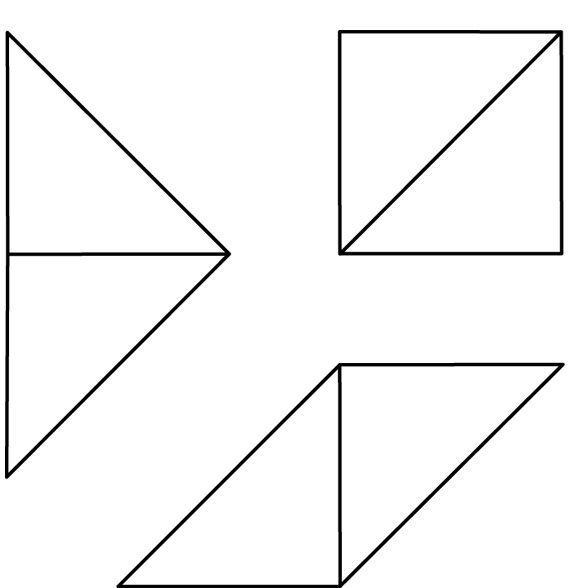
Figure 4 shows the only three shapes that can be made.
The triangles used in this lesson are isosceles right triangles with a 2-inch hypotenuse. Students do not need to use these terms, but help them notice that the triangle consists of two congruent angles and one right angle. Students should also notice the triangle has a longer side (hypotenuse) and two shorter sides that are congruent (same length).
Same and Different: Flips, Turns, and Congruence. The three shapes in Figure 4 are all that can be made if turns and flips are not counted as different. This rule follows common mathematical convention: shapes that are congruent are usually understood to be “the same.” This rule conveniently limits the number of different shapes that are possible, but it may also confuse some students. Although the shape in Figure 5 is a square, many students would say that it is a diamond and not a square because it is turned from the standard position.
Build and Analyze Two Triangle Shapes. Question 6 in the Student Guide gives students directions for recording information about each shape on the Building with Two Triangles page in the Student Activity Book. Display this page.
- Find a shape that can be made with two triangles.
- How many sides does the shape have (Question 6B)?
- How many vertices does the shape have? Counting sides and vertices (Question 6B) is not too difficult although some students may be distracted by the interior triangles. They may claim that shape A in Figure 6 has four or five sides. Explain that in this activity only the outline is to be considered. Drawings like shape B in Figure 6 are easier to analyze.
- How many right angles are in the shape? Counting right angles is tricky (Question 6B). Some students have difficulty understanding what a right angle is. Even if they do, right angles can be hard to pick out among the visual clutter of the interior triangles. Using the corner of a square or a piece of paper is one way to check whether an angle is a right angle.
- How many lines of symmetry are in the shape? In Question 6C, students investigate whether their shapes have line symmetry. Of the shapes they draw in their data table, the square has four lines of symmetry, the triangle has one, and the parallelogram has no lines of symmetry. Students can trace their shapes onto paper, cut them out, and fold them to find lines of symmetry.
- How do you know the shape you found is different from those that have already been entered on the table?

Students can trace the shape built from right triangles on larger paper or glue copies of the small right triangles if sketching the shapes presents an obstacle.
Discuss Question 7 in the Student Guide.
- What do you notice about the data in your data table? Do you see any patterns? (Possible response: I noticed that if my shape had 3 vertices, then I had 3 angles.)
- What do you notice about the size of the angles on your triangle? Were they all the same? (Possible response: I noticed that two angles are equal, the other angle is a right angle.)
- What do you notice about the size of the sides of your triangle? (Possible response: I noticed that two sides are equal, and the third side is longer than the other two sides.)