Display the cylinder and the cone from the Power Solids® set.
- What is the same about these shapes? (Both shapes have curved faces, and circle shape bases.)
- What is different about these shapes? (The cone has one circle shape face; the cylinder has two. The cone has a vertex at the top; the cylinder has no vertices. The cone has one edge and one face. The cylinder has two edges and three faces.)
Edges and vertices. For this unit, students will blend everyday language with mathematical language to define the properties and types of objects in space.
Edges meet at points called vertices. The top vertex of a pyramid or circular cone is often called an apex to distinguish it from the other vertices.
Read and discuss the vignette in Question 6A in the Student Guide. Display a cube model and guide students through both methods of counting the edges on the cube to help them understand that Tara's method is more efficient.
Read aloud Questions 6B–C then ask:
- How can the vertices be counted efficiently? (I know the top and bottom are congruent and each has 4 vertices, so 4 + 4 = 8 vertices.)
- How can the faces be counted efficiently? (The top and bottom make 2 faces, and each has 4 edges so there would be 4 faces connecting them, so 2 + 4 = 6 faces.)
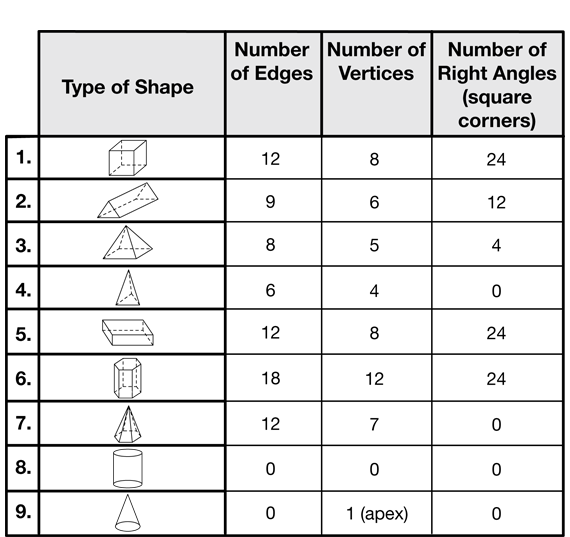
Encourage students to use similar reasoning to complete Question 7 in the Student Guide which asks them to complete the rows for the hexagonal prism, hexagonal pyramid, cylinder, and cone, using the Edges, Vertices, and Faces Table page in the Student Activity Book. Allow students to refer to examples of three-dimensional shapes on display as needed. Ask students to complete the Edges, Vertices, and Faces Table display. See Figure 6.