Tangram Puzzles

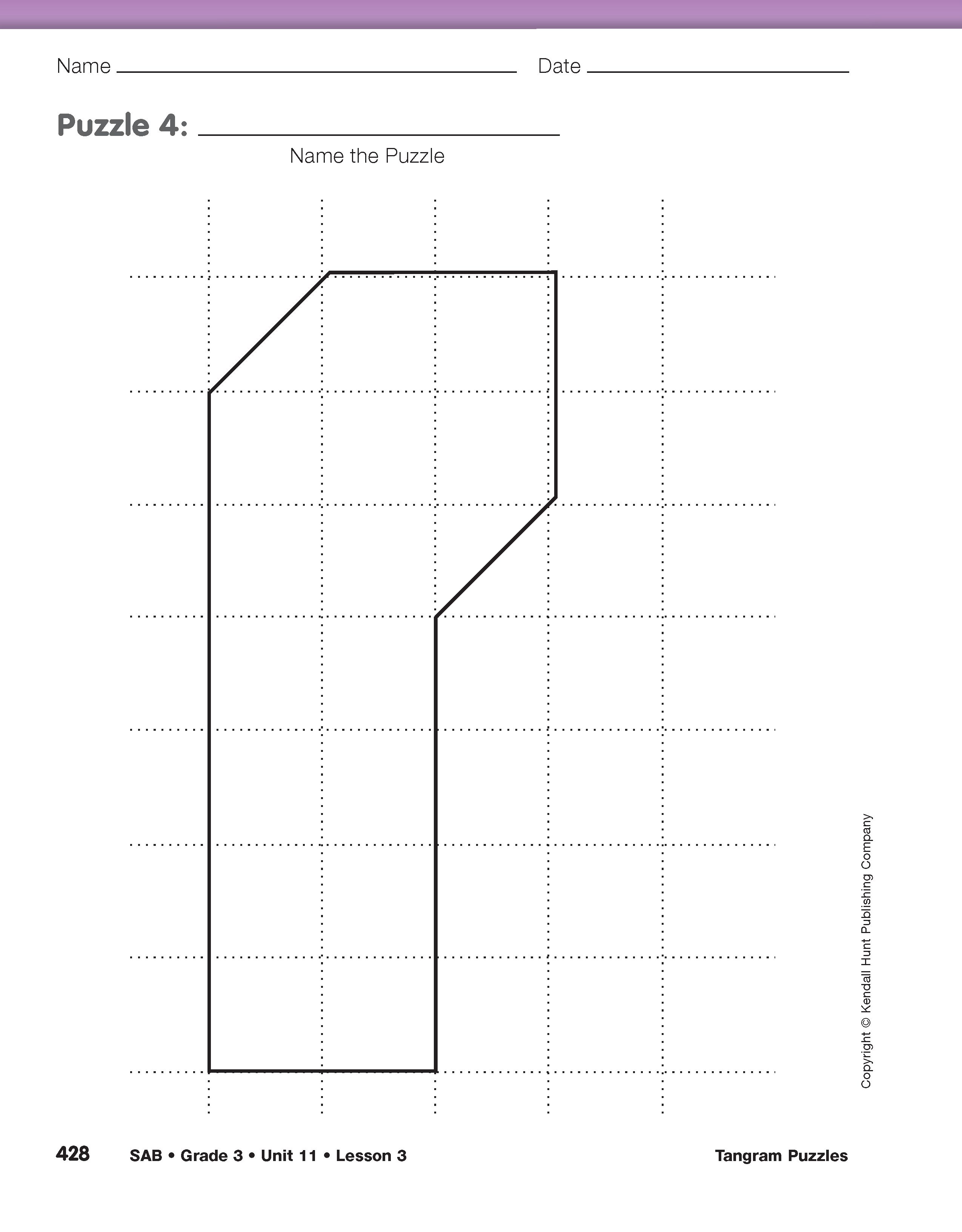
Make Four Puzzles. Ask students to use all seven tangram pieces to solve each puzzle on the Tangram Puzzles 1–4 pages in the Student Activity Book. Some students may give up after a short time. Encourage them to persist. Interesting problems require perseverance. If some students are having trouble after trying for a while, and you have reminded the students about the strategies, give a hint by showing where to place one piece in the puzzle. After students have had a chance to solve each puzzle, ask students to display their solutions.

After students have completed the tangram puzzles, ask the class to compare them.

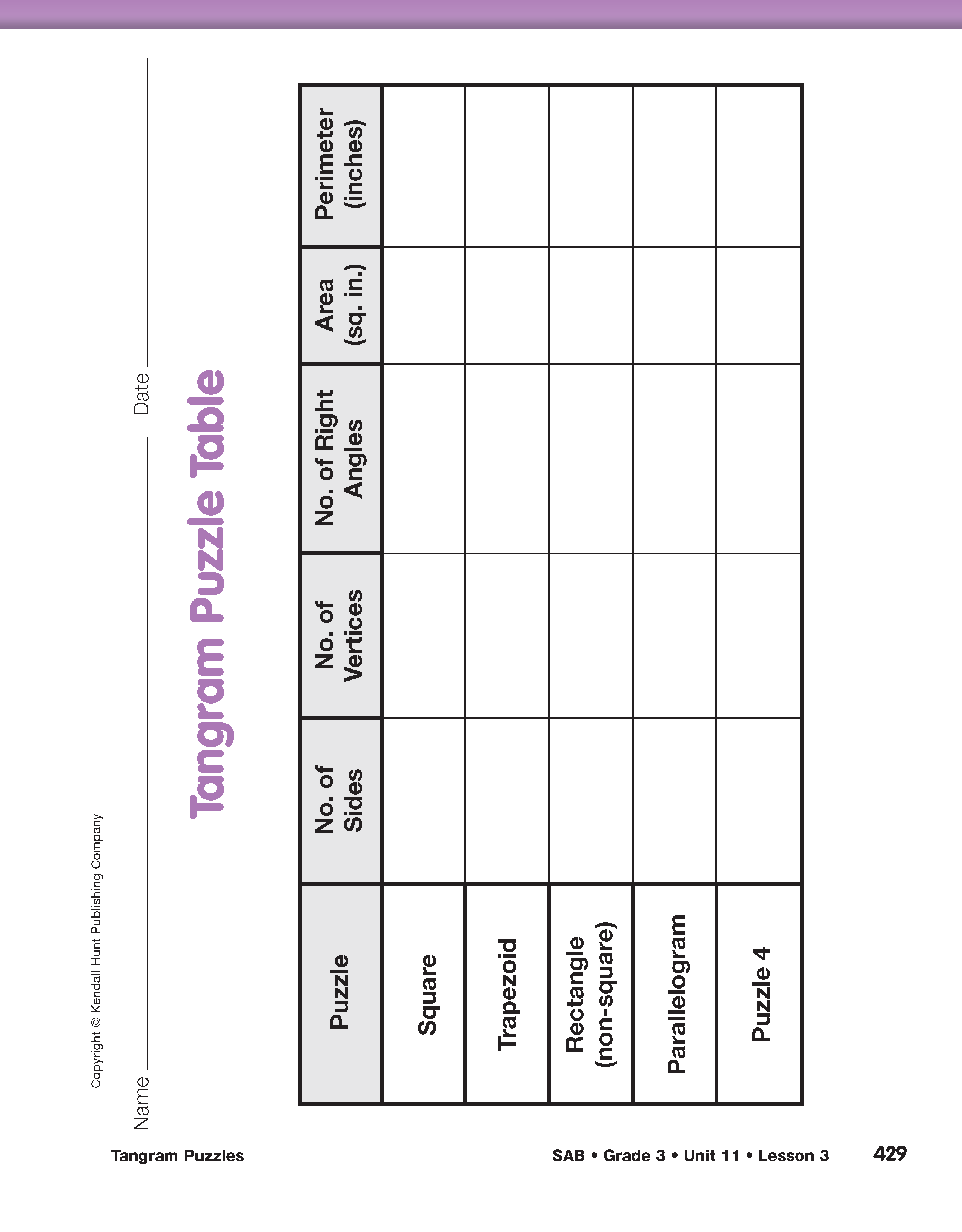
Record Data for the Square. Tell students they will be completing the Tangram Puzzle Table page in the Student Activity Book to better organize their comparisons. You will analyze the square together as a class. Display the Tangram Puzzles page in the Student Guide and place tans within the outline of the square to complete the puzzle.

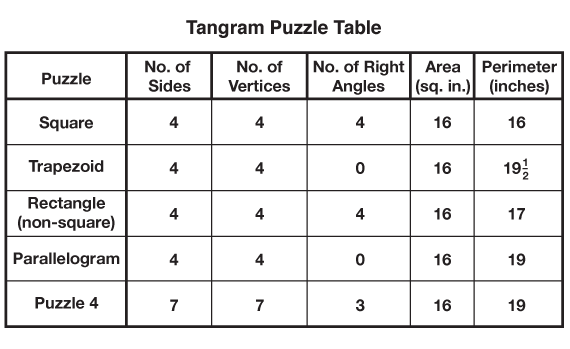
Use the display of the square to review what the terms on each column of the table mean. Ask students to show how they determined the number of sides, vertices, right angles, area, and perimeter. Complete the first row of the table together as you record students' observations and measurements on the Tangram Puzzle Table prepared prior to the lesson. See Materials Preparation and Figure 4 for a completed table.

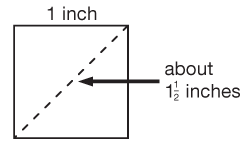
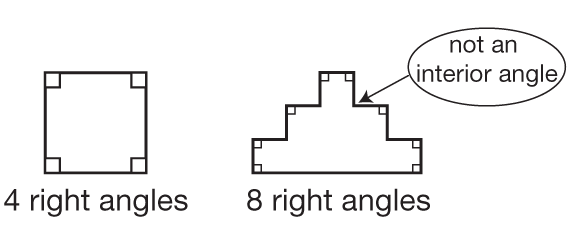
Point out to students that the angles they are finding are inside the outline of the shape. While this may be clear in the analysis of the square, students may want to incorrectly count angles outside of a shape as they look at other tangrams. See Figure 3.

Encourage students to share a variety of strategies for finding the perimeter of the square. Some students will count the perimeter one inch at a time, while others might measure the length of each side of the square and then add the side lengths together.

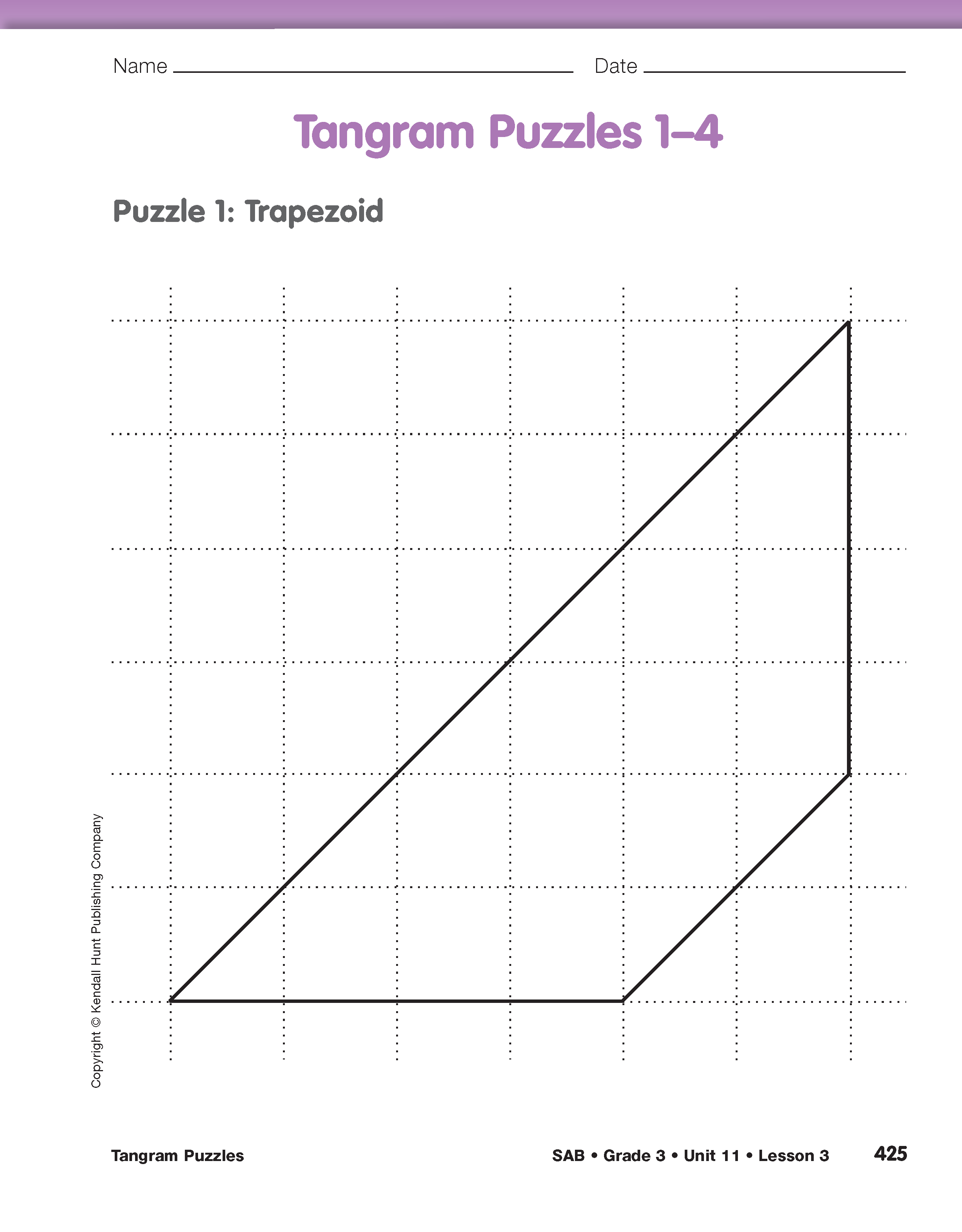
Record Data for the Trapezoid. Display Puzzle 1: Trapezoid from the Tangram Puzzles 1–4 pages in the Student Activity Book. Ask students to look at Puzzle 1: Trapezoid and complete all the columns of the table except for the perimeter.

Measure Perimeter to Nearest Half Inch. To measure the perimeter of these shapes, students will need to practice measuring length to the nearest half inch. Display and refer students to the Measuring Lines page in the Student Activity Book. Students will label every half inch on a picture of a ruler. Then, using their rulers, they will measure the lines to the nearest half inch. To determine the nearest half inch, students need to decide if the measure of the line is closest to 3, 31/2, or 4 inches. Students should compare and verify measurements with a partner. Then ask a volunteer to use the display and an inch ruler to demonstrate how he or she determined the measurement.

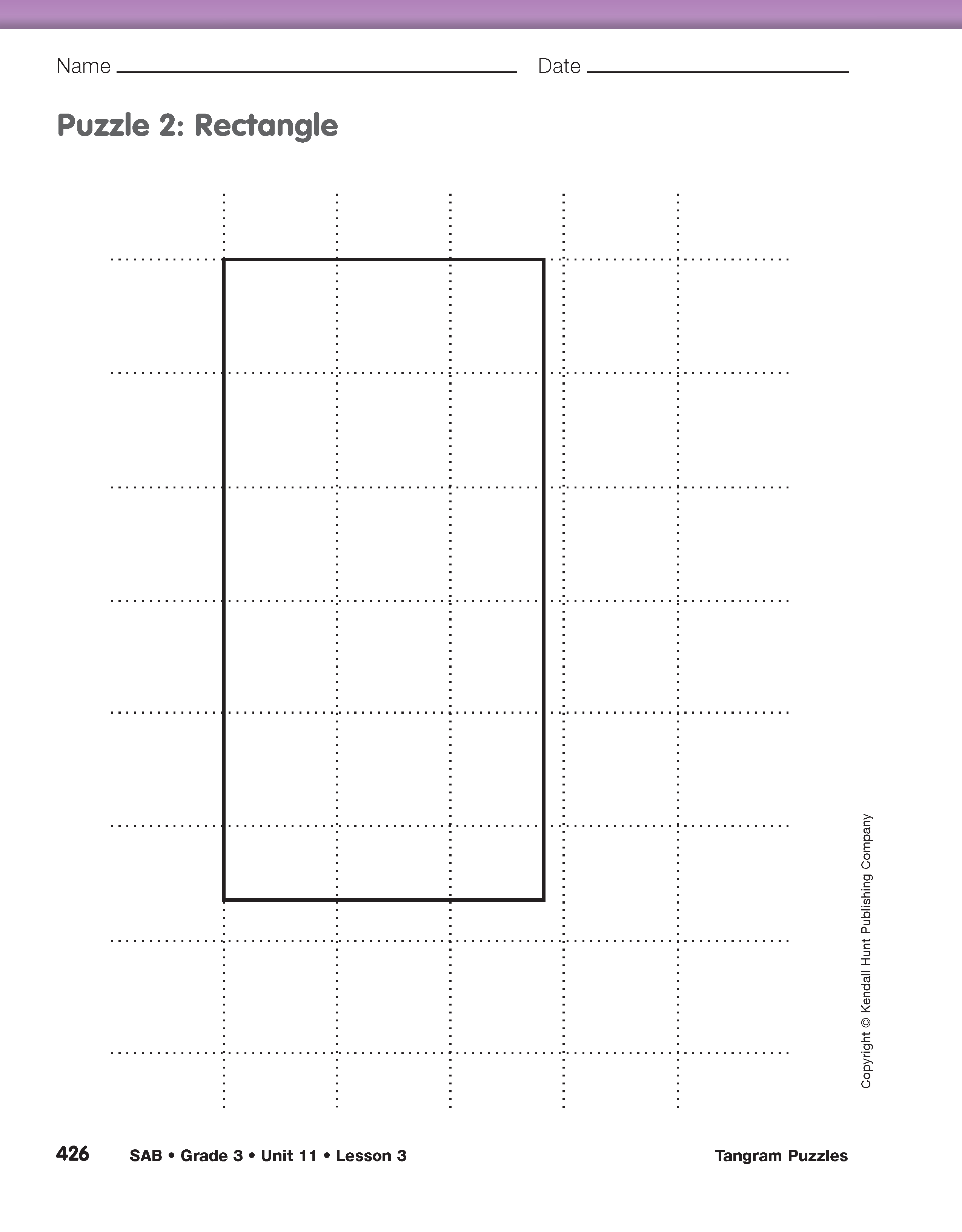
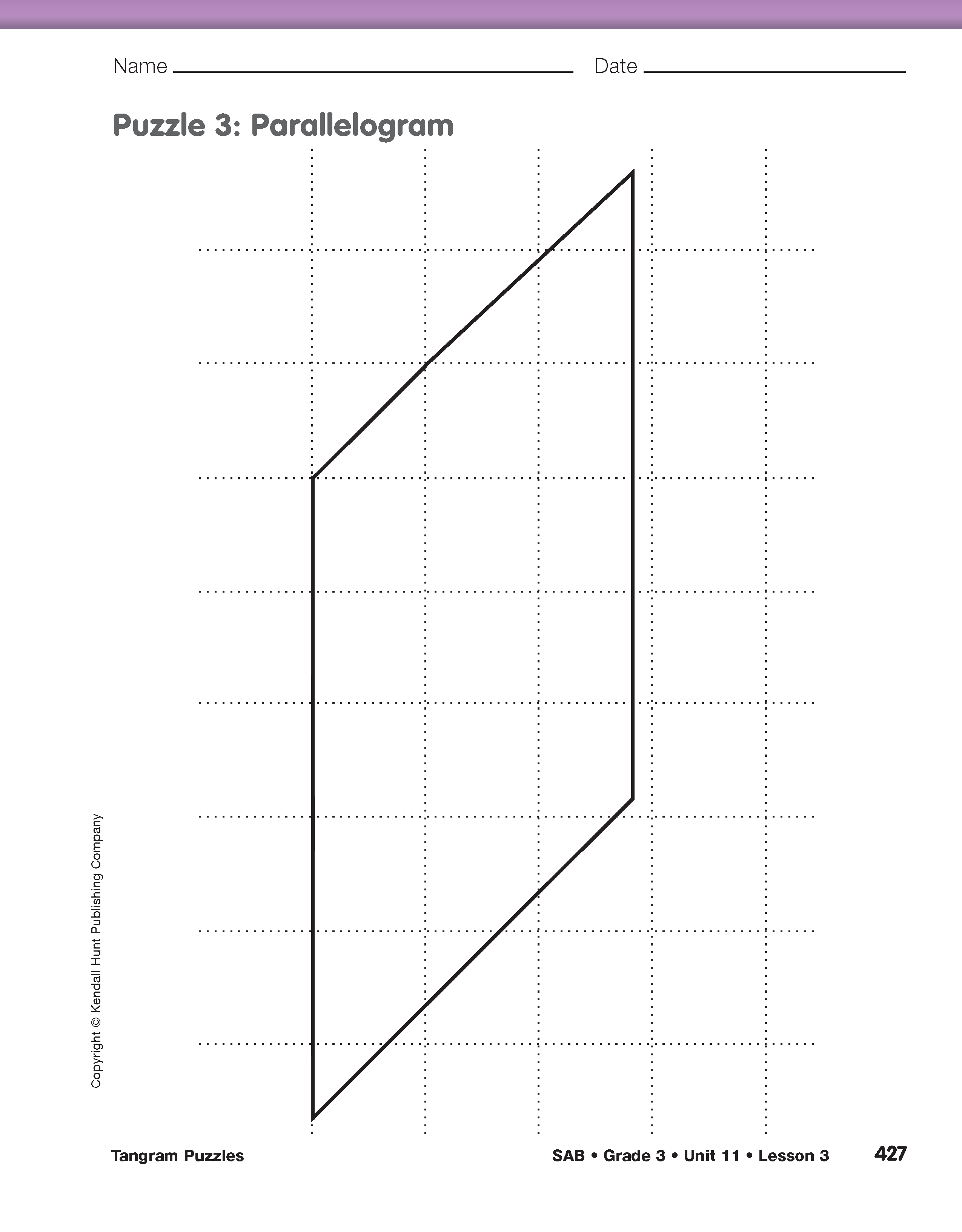
Complete the Table. Ask students to complete the Tangram Puzzle Table for the rest of the puzzles. Perimeter should be measured to the nearest half inch. Encourage students to compare measurements and observations about the puzzle shapes.

Compare Puzzles. Using displays of the Tangram Puzzles 1–4 pages from the Student Activity Book, ask students to share measurements and observations for the trapezoid, rectangle, parallelogram, and Puzzle 4 shape. Complete the class Tangram Puzzle Table as information is shared. See Figure 4.