Describe Strategies for Addition Facts. Tell students
they are going to have a "strategy session"
about addition. Explain that they will solve problems
with sums up to 20 and pay special attention to the
strategies they use. Display the two sheets of chart
paper and the Show Your Strategy Cards with the
facts 6 + 1, 6 + 6, 6 + 7, and 9 + 5. See Materials
Preparation. Focus students' attention on the cards
displayed and ask students to explain how to solve
each problem.
- Look at the addition facts on the four Show Your
Strategy Cards. Who would like to show the class
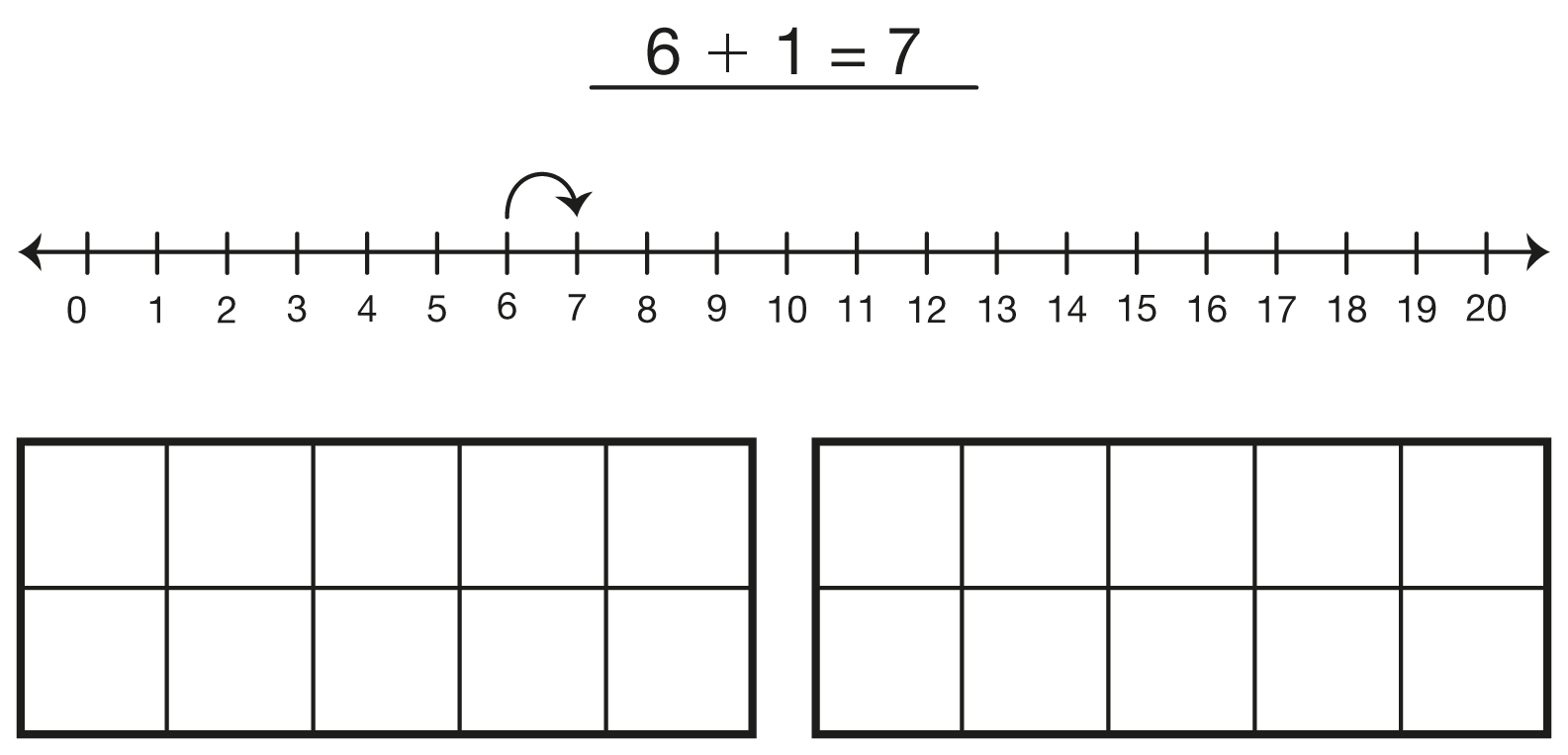
how to solve 6 + 1?
- Describe your strategy. (Possible response: I put 6
in my head and counted 1 more. My answer is 7.)
- What tools did you use to solve the problem?
(Possible response: I used the number line.)
- Describe how you used the tool to solve the problem.
(Possible response: I started at 6 on the number
line and jumped one more.)
As students describe their thinking, ask them to
show their thinking using the tools and space on the
Show Your Strategy Card Display Master. Have connecting
cubes readily available as well. Then, record
that solution on the corresponding card you prepared.
See Figure 2. Repeat this discussion for the
other three facts displayed. Use the blank space on
the card to record strategies that are not supported
with a number line or ten frames.
Students can learn much from each other. By listening to
the strategies of other students and trying them out, they
can become more flexible in their thinking and more effective
problem solvers.
If a student is counting all, ask if there is another
strategy that may be more efficient. See the Sample
Dialog to guide your discussion of strategies.
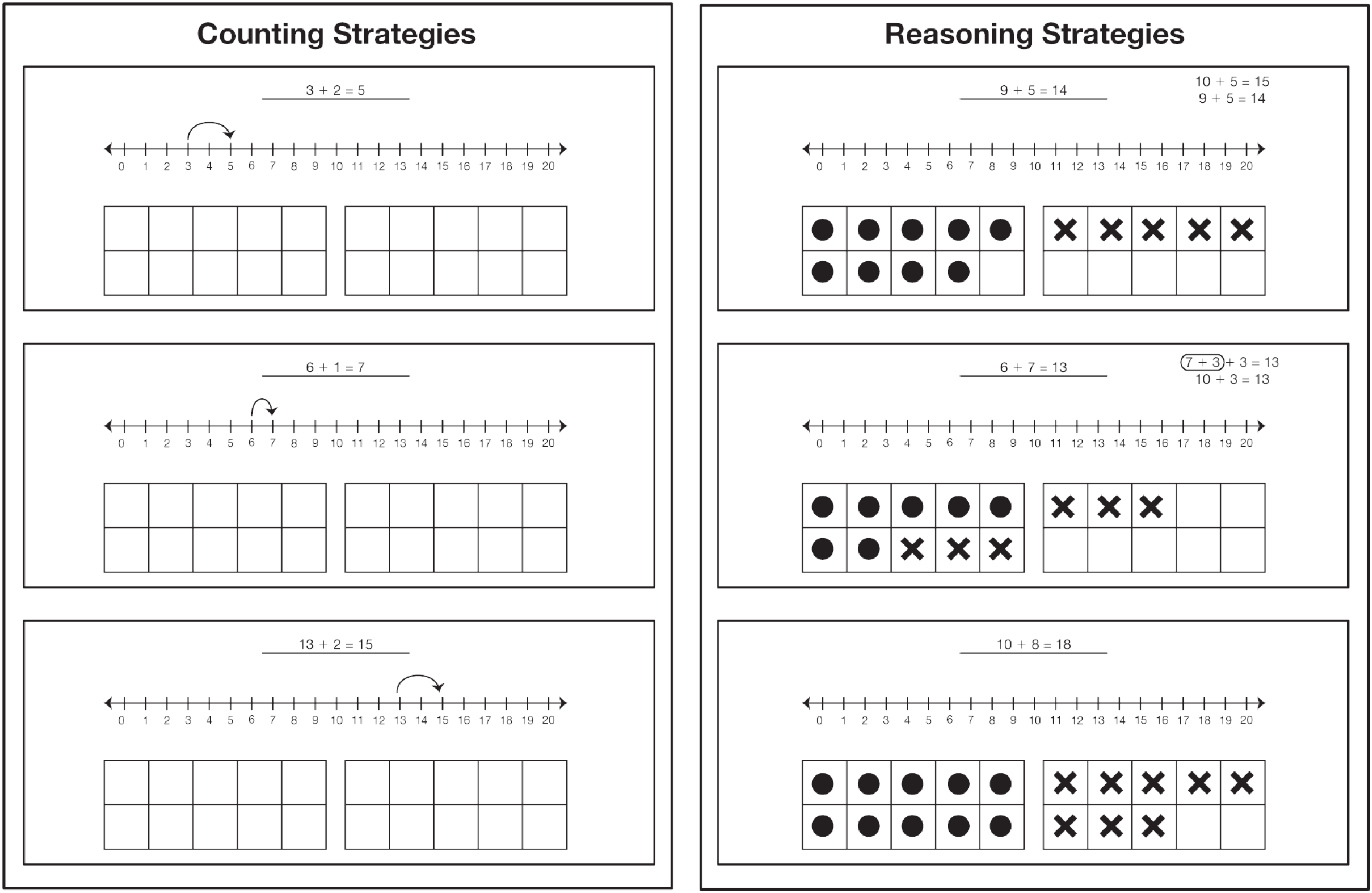
- Now, look at the 2 charts: Counting Strategies and
Reasoning Strategies.
- Who can explain what counting strategies are?
(Possible response: Counting strategies are when
you count to find the answer. For counting on, I
start with the larger number and count on the
smaller number.)
- Who can explain what reasoning strategies are?
(Possible response: Reasoning strategies are
strategies that use what you already know to help
you solve the problem like using doubles and
making tens.)
- Where would you place the fact 6 + 1? (Possible
response: I would put it on the Counting
Strategies chart because we started with 6 and
counted on 1 more.)
- When would you use the strategy counting on?
(Possible response: I would use it if I had to
count on a small number like 1, 2, or 3.)

Use this sample dialog to guide your discussion of strategies.
Teacher: What strategy did you use to solve 6 + 2?
Anna: I counted on my fingers. I counted: 1, 2, 3, 4, 5, 6, and
then, 2 more, 7, 8.
Teacher: Did anyone use a different strategy that is more
efficient?
Jenny: I used counting on. I started at 6 and counted on 2: 7, 8.
Teacher: How is that more efficient than starting at 1?
Jenny: I already know that one of the numbers is 6 and I just
have to count 2 more.
Teacher: Which tools can you use to demonstrate counting
on?
Jenny: I can use the number line. I start at 6 on the number
line and jump two more.
Teacher: Good answer! Now, what strategy would you use
to solve 6 + 7?
Mark: I would use counting on. I would start at 7 on the
number line and count on 6.
Nicholas: I would use a different strategy. I know that
6 + 6 = 12, so 6 + 7 would be one more or 13.
Teacher: That's a good strategy to use for this fact. When
should you use counting on as a strategy?
Jose: I would only use it when you count on small numbers
like 1, 2, or 3.
Teacher: Why wouldn't you use it to count on larger number?
Jose: I think it takes too long to count on numbers like 9, 10,
or 11. It's better to use a reasoning strategy like using
doubles or making tens.
Teacher: Which tools can you use to demonstrate using
doubles?
Jose: I can make two trains of connecting cubes with 6 each.
That makes 12. If I add one more connecting cube to
one of the trains, that one will have 7 and I'll have
13 cubes.
Teacher: What strategy would you use to solve 8 + 9?
Jason: I would use the strategy using doubles. I know that
8 + 8 = 16, so 8 + 9 = 17.
Teacher: That's an efficient strategy. Did anyone think of
another strategy?
Gina: I used the strategy using ten. I know that 8 + 10 = 18,
so 8 + 9 is one less or 17.
Teacher: That's another great strategy to use! Sometimes,
we can use more than one strategy to solve a problem,
but we want to try to use a strategy that is efficient.
Post the Show Your Strategy Card on the appropriate
chart. See Figure 3. Focus students' attention back
on the remaining three Show Your Strategy Cards.
- Would you use the strategy counting on for any of
these other facts? (Possible response: No,
because for the other facts you have to count on
more than 1, 2, or 3.)
Naming Strategies. There are many different ways to name a
strategy. Encourage students to use names that are meaningful
and will help them remember the strategy. Names can be
related to the steps in the strategy like counting back or
counting up. Names can also be selected because students
associate the strategy with a particular student in the class
who regularly uses a strategy. It is not important that students
be able to name the strategy, though it does help them
discuss and distinguish them.
Have students focus their attention on the Show Your Strategy Card with the addition facts 6 + 6 and
6 + 7.
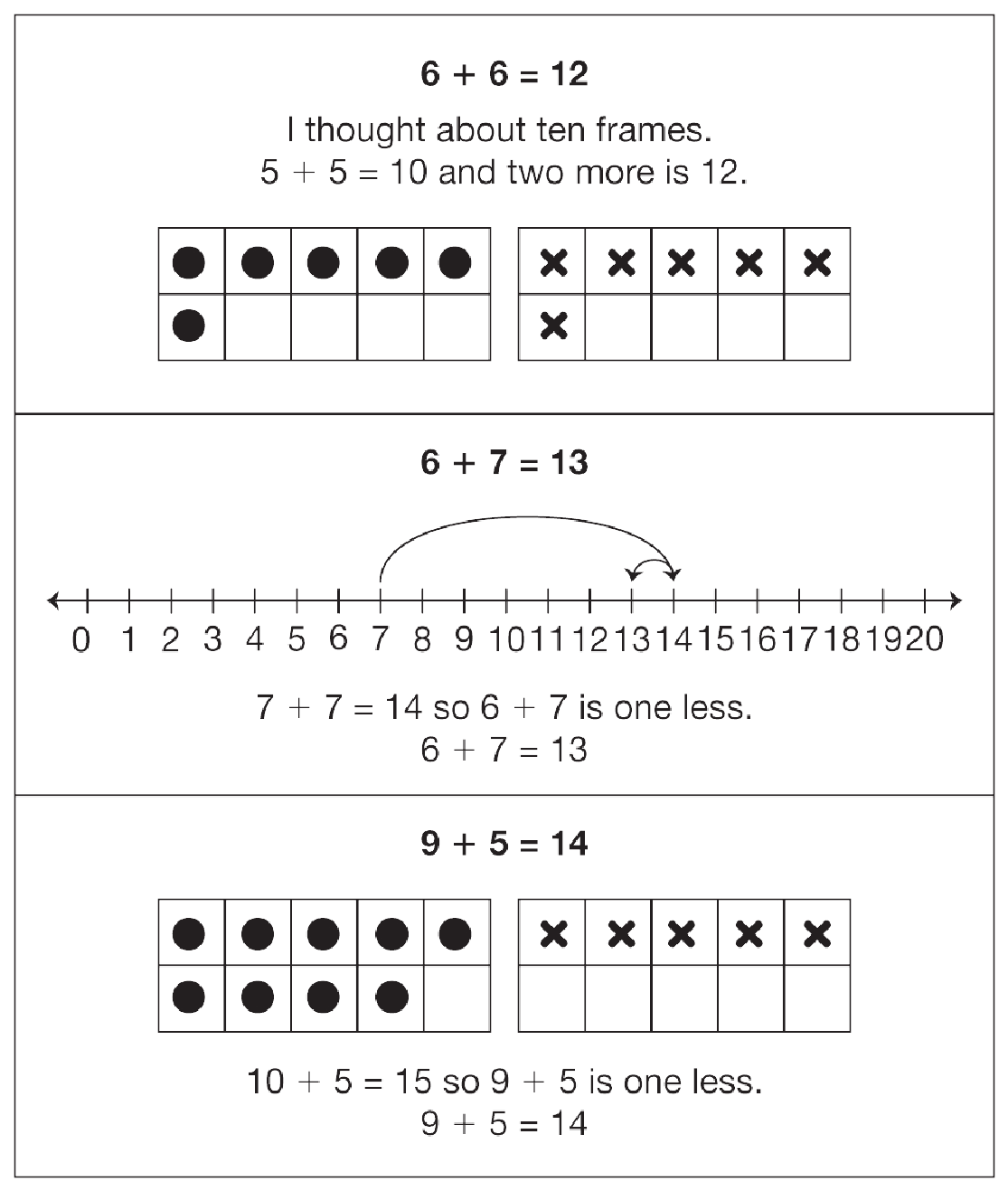
- What strategy would you use to solve 6 + 6?
(Possible response: That's a doubles fact because
it has the same two numbers. Knowing a doubles
fact is a reasoning strategy.)
- If you know 6 + 6, how can you use that fact to
solve 6 + 7? (Possible response: I know that
6 + 6 = 12, so 6 + 7 is one more or 13.)
- Describe the using doubles strategy. (Possible
response: If you know your doubles, like 6 + 6,
then you can use them to help you solve a fact
that is near a doubles fact. For 6 + 7, you're just
adding one more to the doubles answer.)
- Is using doubles a counting strategy or a reasoning
strategy? Why? (Possible response: It's a reasoning
strategy because you're using what you
know about doubles to solve it.)
- What if you do not know the double? How can you
figure it out? (Possible response: Use other facts
that you know. For example, I know 5 + 5 = 10
so 6 + 6 is two more or 12 because I need to add
one to each five to get six.)
Record students' solutions for 6 + 6 and 6 + 7 and
place the cards on the Reasoning Strategies chart.
Focus students' attention on the remaining card:
9 + 5.
- What strategy would you use to solve 9 + 5?
(Possible response: I would use the strategy
using ten.)
- Describe the using tens strategy. (Possible
response: I know that 10 + 5 is 15, so 9 + 5 is one
less or 14.)
- On which chart should I place 9 + 5 and why?
(Possible response: It's a reasoning strategy.
You're using what you know about adding ten to
solve it because 9 is one less than 10.)
Record the solution for the remaining card and place
it on the appropriate chart.
Sort Addition Facts on Show Your Strategy Cards. Have students work in groups to discuss
strategies for the remaining Show Your Strategy Cards. Give 4–5 facts to each group, and as they finish,
you may give them additional facts to solve. Ask
each group to solve the addition facts and show their
strategy on the number line, ten frames, or with a
drawing or number sentences. As groups complete
their cards, have them attach the cards to the chart
that corresponds to the strategy that they used to
solve the problem.
- What strategy did you use?
- What tools did you use or think about to solve the
problem? (number lines, connecting cubes, ten
frames, drawings)
- Should you place your card on the Counting
Strategies or Reasoning Strategies chart?
Some students may have trouble naming their strategy.
Allow students to place their card on the chart
they think is appropriate. If they do not choose the
appropriate chart, there will be a chance to rearrange
the cards later.
Discuss Counting and Reasoning Strategies. Upon
completion, direct students' attention to the addition
facts on the Counting Strategies and Reasoning
Strategies charts.
- When does it make sense to use a counting strategy?
(Possible response: when you are adding a
small number like 1, 2, or 3)
- Does it make sense to use counting to solve all the
facts we placed on the Counting Strategies
chart? (Possible response: No, we want to use a
strategy that is quick and accurate. We don't want
to use counting to add on large numbers.)
- Are there facts that you would like to move from
this chart to the other chart? Why? [Students may
want to move some of the facts to the Reasoning
Strategies chart.]
Direct students' attention to the facts on the
Reasoning Strategies chart. Have a few students
share their reasoning strategies.
- What strategy did you use to solve [9 + 5]? (Possible response: I know that 10 + 5 = 15, so
9 + 5 is one less or 14.)
Students have been inventing and using counting strategies
to solve problems using addition throughout First Grade. In
this lesson, students will focus on deciding which strategy is
more efficient for a given problem. Students will also explore
reasoning strategies (doubles, using ten, using doubles,
making ten). This lesson provides practice and attention to
the counting and reasoning strategies.
Find a few of these facts on the Reasoning Strategies
chart. Record a name of this strategy (e.g., using ten,
making ten, using doubles) and place these facts
near that name. You may need to add chart paper.
Repeat this process for other reasoning strategies. As
the class rearranges the cards, some students may
decide that some addition facts can be placed under
more than one strategy.
- Can you use more than one strategy for some of
these facts? (Possible response: For 9 + 9, you
can use the using ten strategy. I know
10 + 9 = 19, so 9 + 9 = 18. I could also use the
doubles. I know 8 + 8 = 16 so 9 + 9 is two more
or 18.)
Compare to Addition Strategies Menu. Display
and ask students to refer to the Addition Strategies
Menu for the Facts in the Student Activity Book. See
Figure 5. Ask students to compare the Addition
Strategies Menu for the Facts to the strategies they
collected on the charts.
- What is the same?
- What is different?
- Are there any strategies that you would like to add
or change? (Possible response: Doubles and
adding zero are reasoning strategies that are not
on the chart. Adding zero is a reasoning strategy
because we know that adding zero doesn't
change the number.)
- Are there strategies on the menu that were not on
our charts?
Have students add other strategies they think of to
the Another Strategy box on the menu or to the back
of the menu.