Welcome to Second Grade
Learning through Problem Solving
"Solving problems is not only a goal of learning mathematics but also a major means of doing … read more
Learning through Problem Solving
"Solving problems is not only a goal of learning mathematics but also a major means of doing so. … Problem solving is an integral part of all mathematics learning, and so it should not be an isolated part of the mathematics program" (NCTM, 2000). In this unit, data collection and analysis provide rich contexts and concrete models to support students' problem solving and reasoning. There is evidence that young students bring to school a wealth of informal mathematical knowledge and strong problem-solving capabilities. This suggests that students are able to solve many kinds of problems in familiar contexts, particularly when they can use manipulatives, drawings, and their own ways of thinking. "When the teaching and learning of mathematics is approached from a problem-solving perspective, concepts and procedural skills are developed on the basis of problem settings that require those concepts and skills. A problem-solving approach helps young children make sense of the concepts, skills, and relationships that are essential in an early childhood mathematics curriculum" (Worth, 1990).
It is important that students encounter a range of different kinds of problems. The work of Thomas Carpenter and his colleagues (Carpenter, Fennema, and Peterson, 1987; Carpenter, Carey, and Kouba, 1990) with the Cognitively Guided Instruction Project (CGI) provides insights that can help teachers with this process. They devised a classification scheme for problems most adults would solve by addition, subtraction, multiplication, or division. CGI classifies the addition and subtraction situations into 11 types of problems. Research by the CGI Project and others has shown that certain types of problems are more challenging than others. Traditionally, just two of the 11 addition and subtraction types have dominated elementary mathematics textbooks in the United States. Moreover, these favored problem types are the easiest to solve. Most of the addition problems that elementary students encounter are classified as "join—result unknown." For example, there are three corn plants in one row and two plants in another row. How many plants are there? Similarly, most of the subtraction problems are "separate—result unknown." For example, a farmer had 8 carrots and a rabbit ate 6 of them. How many carrots did the farmer have left? With such a limited variety of problems, students develop a limited conception of addition and subtraction and also a limited number of problem-solving strategies. The following are example of the problem types:
Join
- Levi wants to buy a sticker and a pencil. How many pennies does he need? (result unknown)
- Levi spent 8 cents on 2 items. One item was 4 cents. How much did the other item cost? (change unknown)
- There is a herd of elephants. Three baby elephants were born. Now there are eight. How many elephants were in the herd at the start? (start unknown)
Separate
- Sam has 7¢. He wants to buy a pencil. How much money will he have left? (result unknown)
- There were ten toads sitting near a pond. Some jumped away. Four toads are still sitting near the pond. How many toads jumped away? (change unknown)
- The company of parrots had some peanuts. They ate five peanuts. Now they have two peanuts left. How many peanuts did the company of parrots have to start with? (start unknown)
Part-Whole
- A pod of whales has three males and eight females. How many whales are in the pod? (whole unknown)
- There are nine birds at the feeder. Three of the birds are yellow canaries and the rest are sparrows. How many sparrows are at the feeder? (part unknown)
Comparison
- One litter has seven kittens. Another litter has five kittens. How many more kittens does the first litter have? (difference unknown)
- One flock of sheep has five lambs. The second flock has eight more than the first flock. How many lambs does the second flock have? (quantity unknown)
- There are twelve geese in the pond. This is five more than the number of geese on the grass. How many geese are on the grass? (referent unknown)
Students must be allowed sufficient time to solve problems in their own ways. They need to be able to support their thinking with a variety of tools and be encouraged to find a variety of solution strategies. The opportunity to share mathematical thinking is crucial in creating a classroom climate in which students explore, share, and think critically about their problem-solving strategies and those of others. As stated in the Math Practices of the Common Core Standards for Mathematics, "Students at all grades can listen or read the arguments of others, decide whether they make sense, and ask useful questions to clarify or improve the arguments." Teaching about problem solving is part of the instructional fabric of Math Trailblazers. Students engage in problems or tasks that promote a productive struggle and are used to promote conceptual development. The Math Practices page in the Student Activity Book Reference section and shown in Figure 1 provides a framework to focus discussions and make the problem-solving process explicit.

Figure 1: Math Practices
Math Facts Strategies in Second Grade
In this unit, students focus on further developing their understanding of addition and … read more
Math Facts Strategies in Second Grade
In this unit, students focus on further developing their understanding of addition and subtraction. Specifically, students are asked to grapple with moving from less efficient (direct modeling and counting strategies) to more efficient reasoning-from-known-facts strategies. Students have been gaining fluency with the partners or partitions of ten and the facts that are efficiently solved with counting strategies. Students will use this knowledge to develop strategies for problems with larger sums (e.g., 6 + 7 or 8 + 9).
Development of Math Facts Strategies
In accordance with the National Council of Teachers of Mathematics Principles … read more
Development of Math Facts Strategies
In accordance with the National Council of Teachers of Mathematics Principles and Standards for School Mathematics, the Curriculum Focal Points (NCTM 2000, NCTM 2006) and the Common Core Standards for Mathematics, Math Trailblazers students are expected to achieve fluency with the addition and subtraction facts by the end of Second Grade. Students work toward this goal by solving addition and subtraction problems in ways that make sense to them. Students also approach the math facts by systematically developing efficient strategies for the facts that will help them learn other facts. For example, the facts with sums of ten (e.g., 8 + 2 and 6 + 4) can help develop make-ten strategies for solving facts with larger sums (e.g., 8 + 7 and 6 + 8). There is a body of research that supports students working toward math facts fluency in this manner.
Generally, students move through three developmental stages when acquiring operational understanding and fluency with the math facts:
- Direct modeling, in which students re-create the action in the problem using manipulatives;
- Counting strategies, such as counting on and counting back; and
- Reasoning from known facts, in which students work from facts they already know. If, for example, a student knows that 6 + 4 = 10, then he or she has a quick way to access 7 + 4 (Carpenter, 1999, National Research Council, 2001).
Throughout the curriculum, students are encouraged to invent their own strategies and to share their thinking with one another. However, particular emphasis is given to specific reasoning strategies. In this unit, students will sort the addition and subtraction facts by strategy (counting or reasoning) to help them think critically about choosing strategies that are efficient for a given problem. From these discussions, they develop a menu of addition strategies for the facts and a menu of subtraction strategies for the facts. The Addition Strategies Menu for the Facts in shown in Figure 2. The Subtraction Strategies Menu for the Facts can be found in the Reference section of the Student Activity Book.
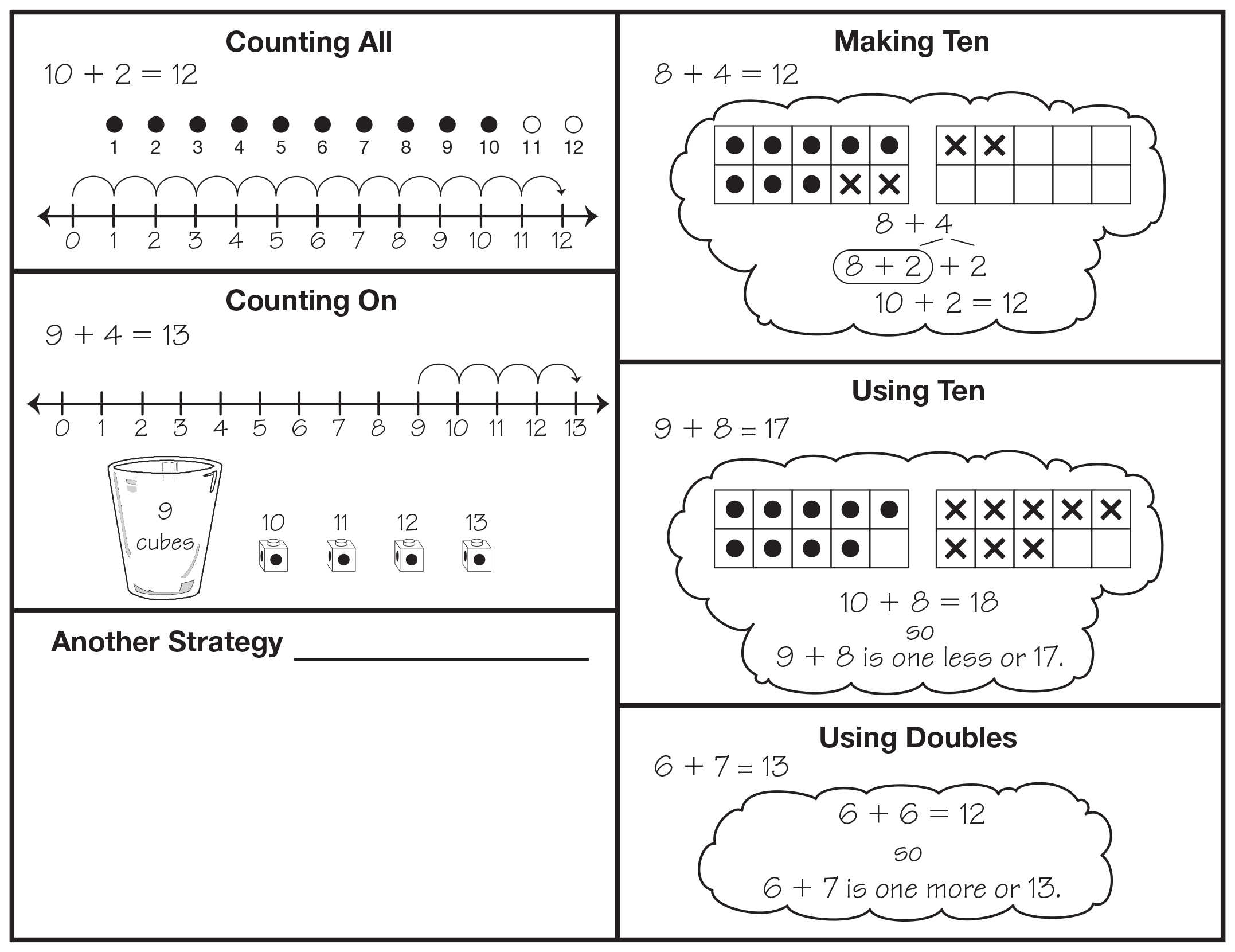
Figure 2: Addition Strategies Menu for the Facts
Reasoning Strategies
Throughout the curriculum, students are encouraged to invent their own strategies and to share their … read more
Reasoning Strategies
Throughout the curriculum, students are encouraged to invent their own strategies and to share their thinking with one another. However, particular emphasis is given to specific reasoning strategies. Students need to be fluent with some strategies to be able to use facts to reason the solutions of other facts. In First Grade, students focused their attention on gaining fluency with the addition facts with sums to ten, partitioning ten into two parts, and learning their doubles. This allows students to use these known facts to find the solution to other facts. It is important that students develop a variety of strategies to gain fluency with smaller numbers. Students will also build on these strategies when working with multidigit numbers in later units. So, throughout this unit and future Second-Grade units, you will have multiple opportunities to observe students solving problems using these strategies.
Using Doubles
Doubling is a natural and appealing strategy that some young students develop before entering school. It is … read more
Using Doubles
Doubling is a natural and appealing strategy that some young students develop before entering school. It is not unusual, for example, for young students to simply announce that "I know that 3 and 3 is 6" or "5 and 5 is 10." Students naturally extend their knowledge of doubling to multiples of 10 and other larger numbers.
Doubling is useful in learning other basic facts. Students readily understand that the sum of 5 and 6 is 1 more than 5 and 5 and, therefore, use a known double to find the answer to a related fact called a near double. Many students make other uses of doubles. Some students find the answer for 5 + 7 by counting 2 more from the double 5 + 5, whereas others use 6 + 6 to find the answer. Doubles are also useful for related subtraction facts. Many students, for example, respond quickly without counting for subtraction facts that involve a double, such as 8 − 4 and 12 − 6. Using doubles also seems to be useful with large numbers such as 40 + 40 or 25 + 25.
An idea closely related to doubling a number is finding half of a number, or halving. Knowing that 10 and 10 is 20 provides a natural bridge to determining that 10 is half of 20. While students' initial classroom experiences with doubling and halving often involve using manipulative materials, they are also able to work with these ideas mentally. Finally, working with doubling and halving numbers builds conceptual readiness for multiplication.
Making Ten
This is a second and very important strategy developed in this unit. Because this strategy is based … read more
Making Ten
This is a second and very important strategy developed in this unit. Because this strategy is based on composing and decomposing ten and other numbers, students will be able to build upon it to help them solve multidigit addition and subtraction problems. Making a ten takes advantage of students' prior experience with partitions of ten when using the ten frame. Students are already familiar with facts that "make ten" such as 8 + 2 and 6 + 4. Students reason from these known facts to find sums for addition facts such as 8 + 5. For the problem 8 + 5, students can first add 8 and 2 to make 10 and then add 3 to 10. See Figure 3.
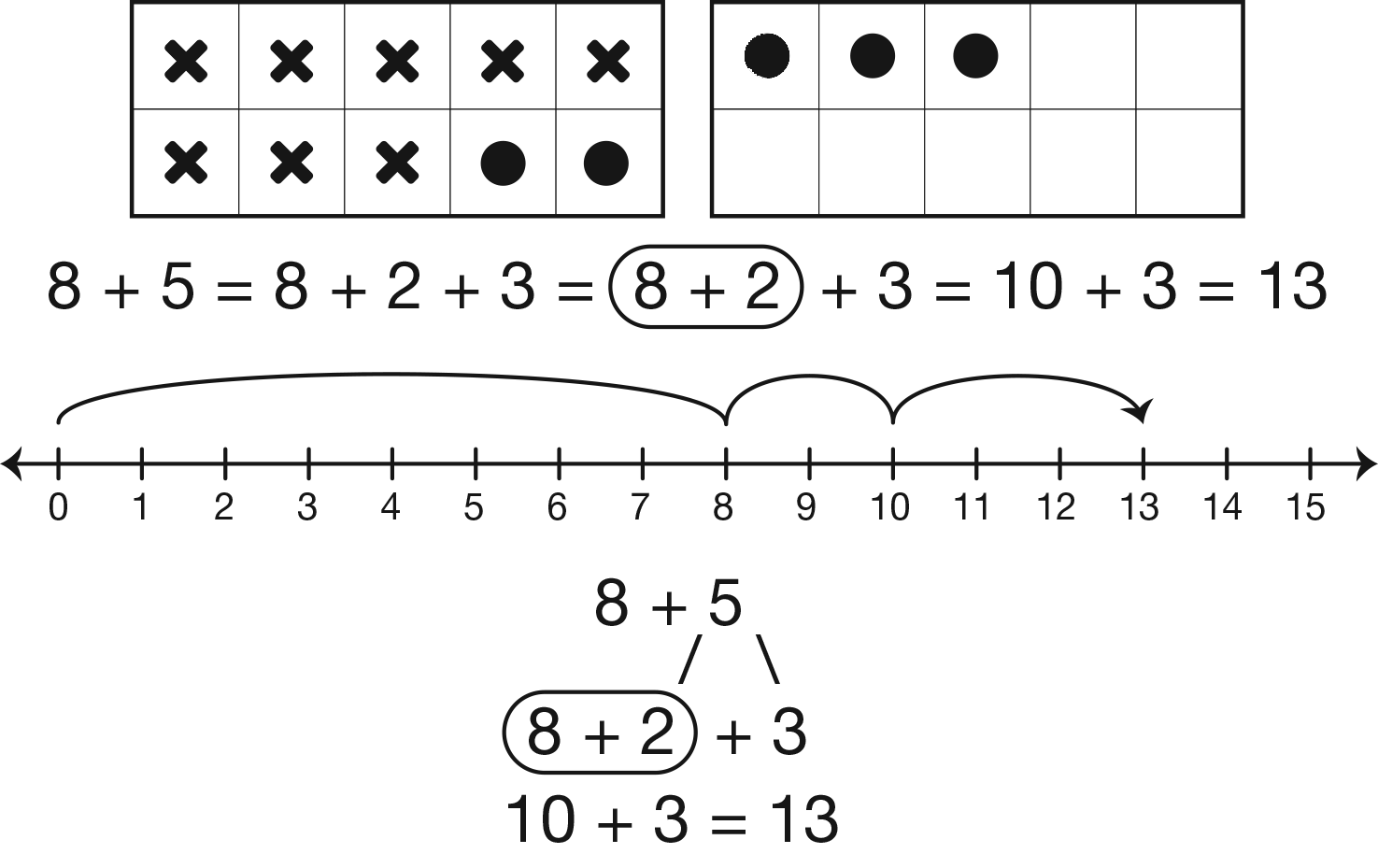
Figure 3: Representations of the making-ten strategy
Representations and Tools
"A significant indicator of conceptual understanding is being able to represent mathematical … read more
Representations and Tools
"A significant indicator of conceptual understanding is being able to represent mathematical situations in different ways and knowing how different representations can be useful for different purposes" (National Research Council, 2001). Students will use number lines, ten frames, and manipulatives as tools for counting, comparing, and communicating their reasoning. These tools help students develop number sense by giving them a concrete and visual representation of the size and order of numbers. These tools also help students use the patterns in the quantity to reason. Students need to have these tools readily available as they work so they can choose the representations that make sense to them and make connections among them. See Figure 3.
MATH FACTS PRACTICE and ASSESSMENT

Practice and assessment of the math facts is based on the results of research in the field. The following … read more
Practice and assessment of the math facts is based on the results of research in the field. The following paragraph from Adding It Up: Helping Children Learn Mathematics published by the National Research Council summarizes much of the literature on practice: "Practicing single-digit calculations is essential for developing fluency with them. This practice can occur in many different contexts, including solving word problems. Drill alone does not develop mastery of single-digit combinations. Practice that follows substantial initial experiences that support understanding and emphasize 'thinking strategies' has been shown to improve student achievement with single-digit calculations" (National Research Council, 2001).
Researchers caution that too much drill too soon can have a negative impact on students' acquisition of the math facts. Studies have shown that "premature practice can be detrimental but that properly managed practice is essential in the development of expertise. … Brief, engaging, and purposeful practice distributed over time is usually most effective" (Brownell & Chazal, 1935; Hiebert, 1999; Isaacs & Carroll, 1999).
Following these recommendations, fact practice in Math Trailblazers is characterized by the distributed practice of small groups of facts that lend themselves to specific strategies. Practice and assessment occur after students have had substantial experiences learning the underlying concepts and developing strategies that make sense to them.
MATH FACTS and MENTAL MATH

The goal of the math facts development in Math Trailblazers is for students to learn the basic math facts … read more
The goal of the math facts development in Math Trailblazers is for students to learn the basic math facts efficiently, gain fluency with their use, and retain that fluency over time. A large body of research supports an approach in which students develop strategies for figuring out the facts rather than relying on rote memorization. This not only leads to more effective learning and better retention, but also to the development of mental math skills. In fact, too much drill before conceptual understanding may interfere with a child's ability to understand concepts at a later date.
The research that contributed to the National Council of Teachers of Mathematics Principles and Standards for School Mathematics and the National Research Council's Adding It Up has informed the structure of the math facts strand in Math Trailblazers. See the Letter Home for more about the development of the basic facts in Math Trailblazers in Second Grade.
Addition Facts
This unit begins a systematic review and assessment of the addition facts to maintain and increase … read more
Addition Facts
This unit begins a systematic review and assessment of the addition facts to maintain and increase proficiency and to learn to apply addition strategies to larger numbers. Students study small groups of facts that can be solved using similar strategies. See Figures 4 and 5.
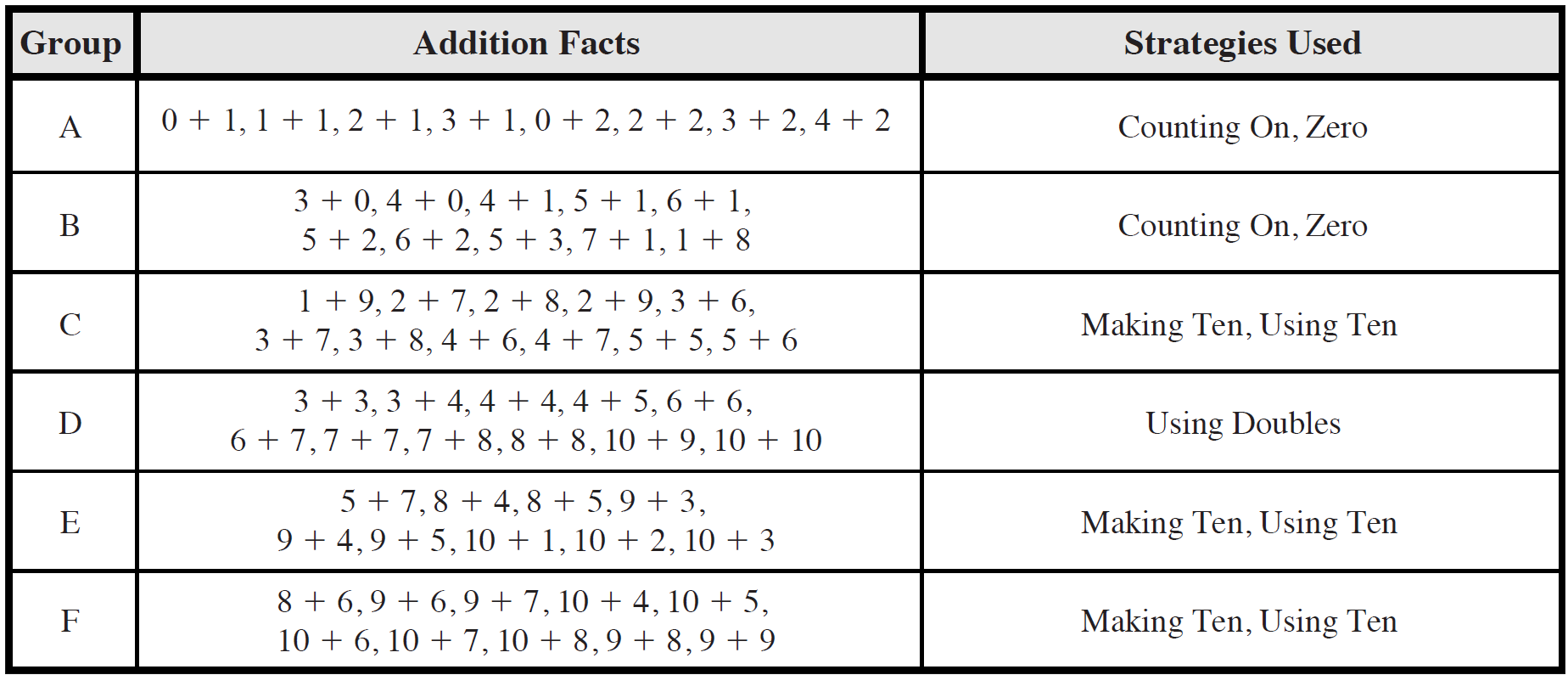
Figure 4: Addition Facts Groups for Grade 2
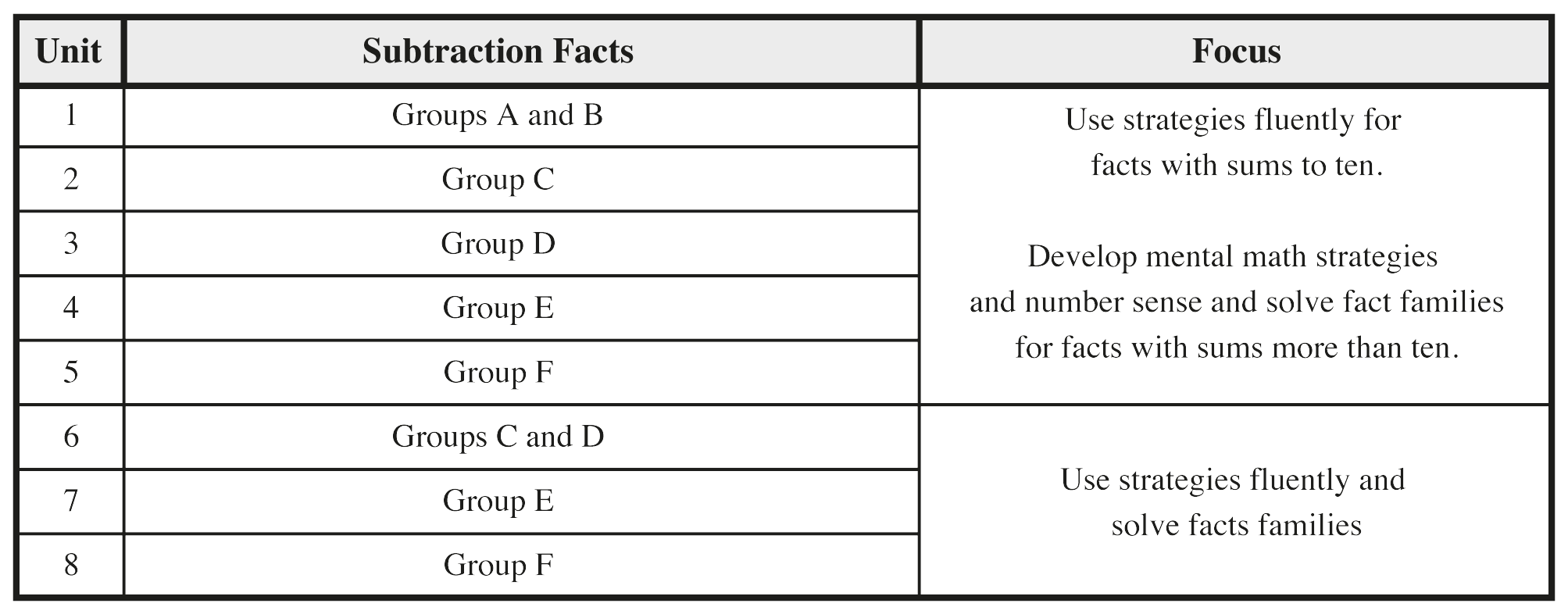
Figure 5: Development of addition facts and the related subtraction facts in Grade 2
Fact Families for Addition Facts with Sums to Ten
Students have been connecting addition to subtraction and using the addition facts … read more
Fact Families for Addition Facts with Sums to Ten
Students have been connecting addition to subtraction and using the addition facts to solve subtraction problems since First Grade. They have also been developing proficient strategies for the addition facts with sums to ten. A student proficient with their addition facts can also find the related subtraction facts. Daily Practice and Problems items in this unit can be used to assess students' abilities to name the fact families related to each fact in Groups A and B.
Resources
- Baroody, A.J. "Why Children Have Difficulties Mastering the Basic Number Combinations and How to Help Them. "Teaching Children Mathematics, 13 (1), pp. 22–31, 2006.
- Bennett, A.B. Jr. and L.T. Nelson. Mathematics for Elementary Teachers: A Conceptual Approach 5th Edition. McGraw Hill, Boston, 2001.
- Brownell, W.A., and C.B. Chazal. "The Effects of Premature Drill in Third-Grade Arithmetic." Journal of Educational Research, 29 (1), 1935.
- Carpenter, T.P., M.L. Franke, and L. Levi. Thinking Mathematically: Integrating Arithmetic & Algebra in Elementary School. Heinemann, Portsmouth, NH, 2003.
- Carpenter, T.P., D.A. Carey, and V.L. Kouba. "A Problem-Solving Approach to the Operations." In Mathematics for the Young Child, J.N. Payne, ed. National Council of Teachers of Mathematics, Reston, VA, 1990.
- Carpenter, T.P., E. Fennema, M.L. Franke, L. Levi, and S.E. Empson. Children's Mathematics: Cognitively Guided Instruction. Heinemann, Portsmouth, NH, 1999.
- Carpenter, T.P., E. Fennema, and P. Peterson. "Cognitively Guided Instruction: The Application of Cognitive and Instructional Science to Mathematics Curriculum Development." In Developments in School Mathematics Education Around the World: Applications-Oriented Curricula and Technology-Supported Learning for All Students. I. Wirszup and R. Streit, eds. National Council of Teachers of Mathematics, Reston, VA, 1987.
- Carpenter, T.P., and J.M. Moser. "The Acquisition of Addition and Subtraction Concepts in Grades One through Three." In Journal for Research in Mathematics Education, 15 (3), 1984.
- Council of Chief State School Officers. Common Core State Standards for Mathematics, 2010.
- Curriculum Focal Points for Prekindergarten through Grade 8 Mathematics: A Quest for Coherence. The National Council of Teachers of Mathematics, Reston, VA, 2006.
- Hiebert, James. "Relationships between Research and the NCTM Standards." Journal for Research in Mathematics Education, 30 (1), pp. 3–19, 1999.
- Isaacs, A.C., and W.M. Carroll. "Strategies for Basic Facts Instruction." Teaching Children Mathematics, 5 (9), pp. 508–515, 1999.
- National Research Council. "Developing Proficiency with Whole Numbers." In Adding It Up: Helping Children Learn Mathematics. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001.
- National Research Council. "Teaching for Mathematical Proficiency." In Adding It Up: Helping Children Learn Mathematics, pp. 181–229. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academy Press, Washington, DC, 2001.
- Principles and Standards for School Mathematics. National Council of Teachers of Mathematics, Reston, VA, 2000.
- Thompson, C.S. "Place Value and Larger Numbers." In Mathematics for the Young Child. J.N. Payne, ed. National Council of Teachers of Mathematics, Reston, VA, 1990.
- Thornton, C.A. "Strategies for the Basic Facts." In Mathematics for the Young Child. J.N. Payne, ed. National Council of Teachers of Mathematics, Reston, VA, 1990.
- Van De Walle, J.A., K.S. Karp, and J.M. Bay-Williams, "Developing Early Number Concepts and Number Sense." In Elementary and Middle School Mathematics: Teaching Developmentally, Eighth Edition. Pearson Education, Inc. Upper Saddle River, NJ, 2013.
- Worth, Joan. "Developing Problem-Solving Abilities and Attitudes." In Mathematics for the Young Child, J.N. Payne (Ed.). National Council of Teachers of Mathematics, Reston, VA, 1990.












