Discuss Different Types of Word Problems. Next
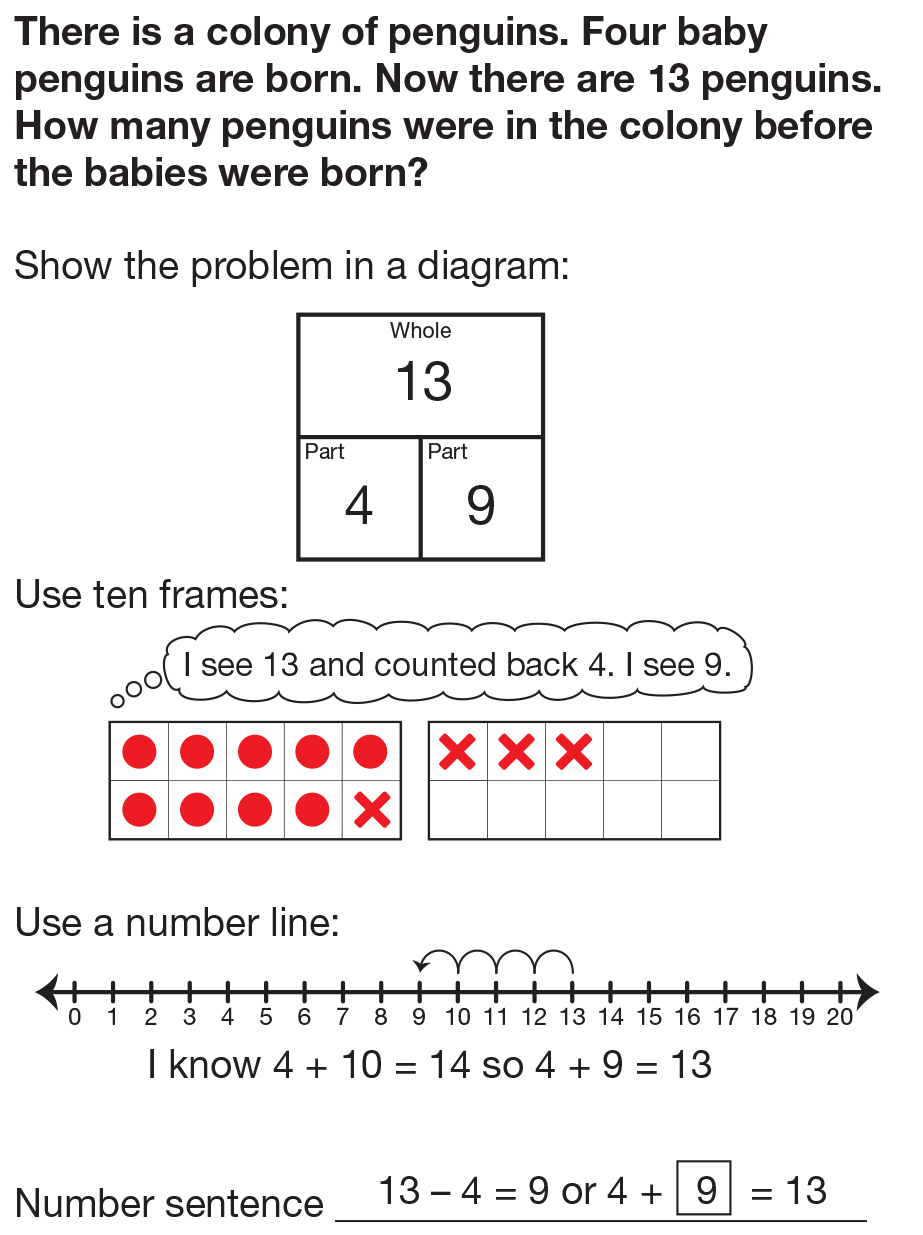
display the penguin problem you prepared on the
Show a Word Problem Master. Ask students to read
the question and work with a partner to solve it.
After students have had a few minutes to talk with
their partners, refer to Math Practice 1, Know the problem, on the displayed Math Practices Reference
page.
- What is the question in this problem? (Possible
response: the number of penguins in the colony
before the babies were born)
Underline the question in the problem. Ask:
- What do you need to do to solve this problem? (Possible response: Subtract 4 from 13; figure out
what I need to add to 4 get 13.)
- What did you do to figure that out? (Possible
response: We acted out the problem with connecting
cubes; we drew a picture of the problem.)
Ask a few students to share and demonstrate how
they know the problem. Then ask a few students to
show how to represent this problem with a part-whole
diagram. See Figure 4.
- [Student name], can you show this problem with a
part-whole diagram?
- How did you decide where to put the 13 penguins? (Possible response: 13 penguins is the whole that
is made up of the babies and other penguins in
the colony.)
Ask students to share their solution strategies for this
problem. See Figure 4.
- [Student name], can you show how you solved this
problem?
- [Student name], please show a different way to
solve the same problem.
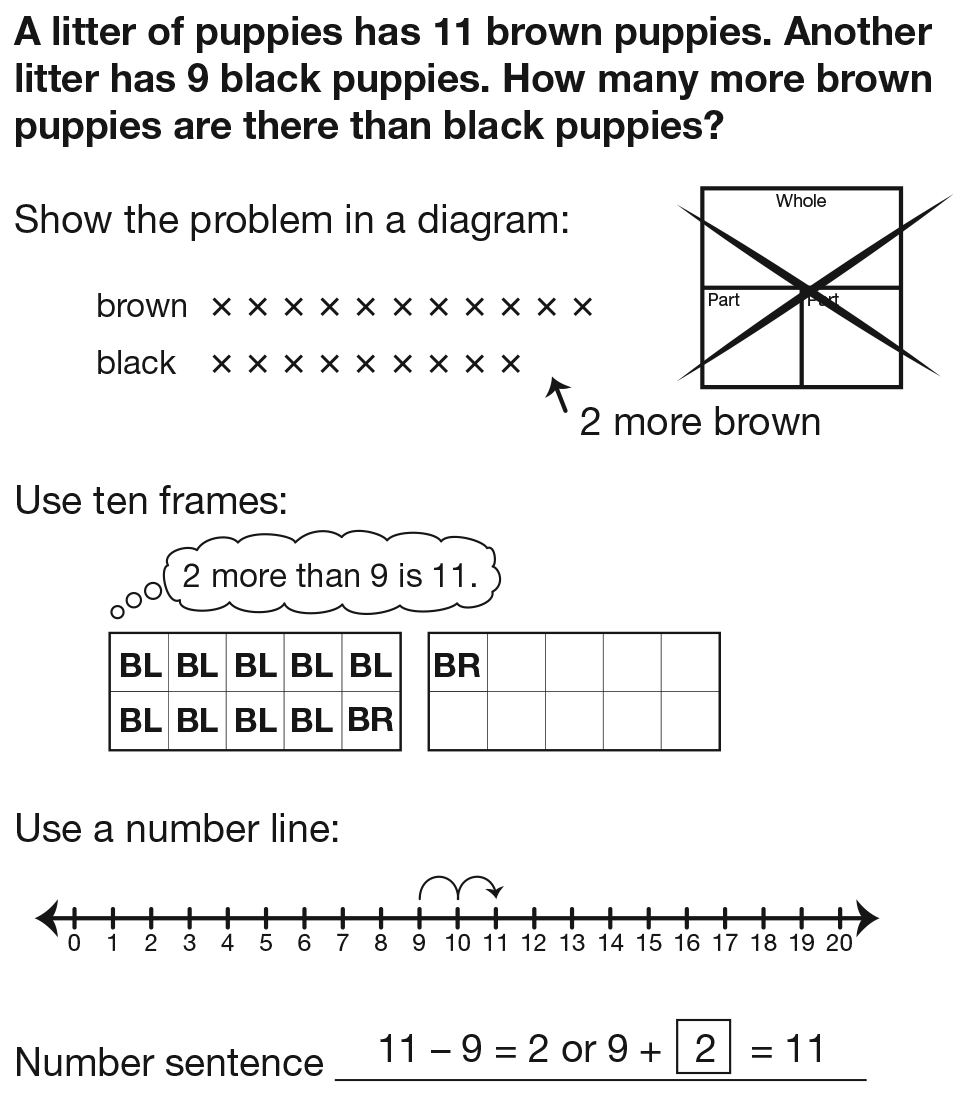
Repeat this discussion using the puppy problem you
have prepared on the display of the Show a Word Problem Master.
- What is the question in this problem? (Possible
response: How many more brown puppies are
there than black puppies?)
Underline the question in the problem. Ask:
- What do you need to do to solve this problem? (Possible response: Compare 11 to 9; find the difference
between 11 and 9.)
- What did you do to figure that out? (Possible
response: We acted out the problem with connecting
cubes; we drew a picture of the problem.)
Ask a few students to share and demonstrate how
they know the problem.
- [Student name], can you show this problem with a
part-whole diagram? (Possible response: No, this
is not a part-whole problem. This is a compare
problem. Neither number shows a whole or part.)
Ask students to share their solution strategies for this
problem. See Figure 5.
- [Student name], can you show how you solved
this problem?
- [Student name], please show a different way to
solve the same problem.
Practice Solving Word Problems with a Partner. Distribute a word problem, markers, and a copy of
the Show a Word Problem Master to each pair of students.
Use the animal word problems you prepared
for each student pair on chart paper. Have scissors
and tape or glue available for each pair of students as
well.
Tell students that they are going to show or tell how
to solve the problem on the chart paper. Remind students
to use the strategies they listed earlier for how
to get to know a word problem. Tell students to show
one strategy for their problem. Others will have a
chance to add other ways of solving the problem
later.
While students are working, circulate using
prompts like:
- What is the question in this problem? [Underline
the question in the problem.]
- What do you need to do to solve this problem?
- What did you do to figure that out?
- Tell me how you solved this problem.
- How did you show that?
- What tool might help you show how you solved
the problem?
Students may choose a ten frame or number line.
They can either draw the tool or use the one on the
Show a Word Problem master you provided.
Students can cut out the tool they used and glue or
tape it to the chart paper.
As students complete their problems, display them
around the room. Once most students are done, tell
them that they are going to solve a different one of
these problems. Assign each pair of students a different
problem displayed. Tell them that they need to
use a different strategy than the first pair of students.
As students are working, circulate looking for interesting
student strategies and for student responses
that do not match.
- Did you get the same answer as the first students?
- Why do you think your answers do not match?
- How did you get to know the problem?
- What strategy did the first students use?
- Did the first students show their work clearly
enough for you?
- What strategy did you use?
- Do you think their work is clear?
- What do you think needs to be added?
- Do you think your work is clear?
Choose a few students to share how they got to know
the problem and how they solved the problem. Leave
these charts displayed for the next part of the lesson.
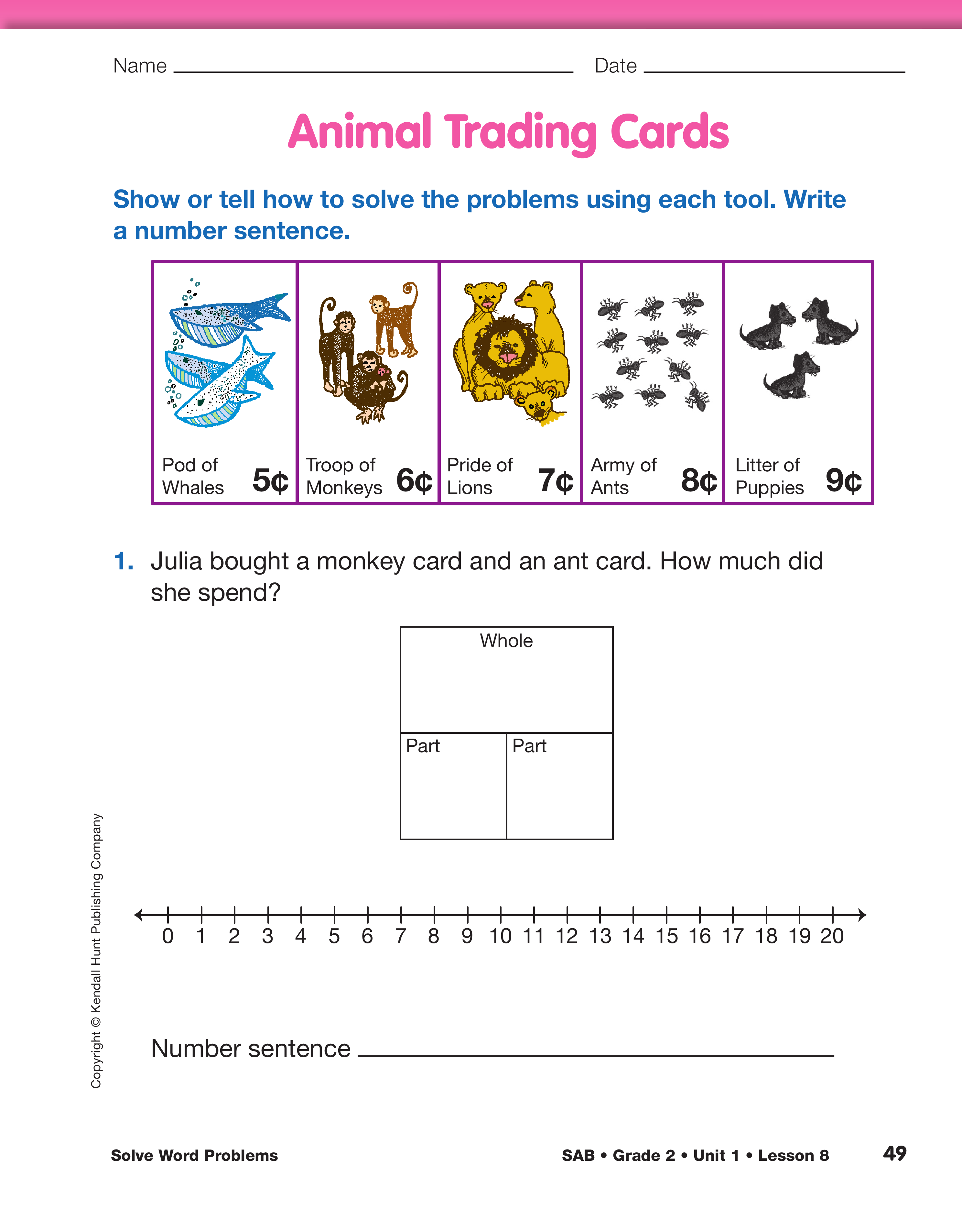
Practice Solving Different Word Problems. Display
the first page of the Animal Trading Cards pages in
the Student Activity Book. Tell students they will
have a chance to practice solving problems while
working with a partner. Explain that the problems are
all about the trading cards displayed at the top of the
page.
- What is a trading card? (Possible response: a card
you collect and trade with others)
- How much does the pod of whales card cost? (5 cents)
- What strategies can you use to solve addition and
subtraction problems? (Possible response: make
ten, count on, use doubles)
Remind students to refer to the Addition Strategies
Menu for the Facts and the Subtraction Strategies
Menu for the Facts they built earlier in the unit.
These can also be found in the Student Activity Book
Reference section.
Have students work in pairs on the Animal Trading
Cards pages and show or explain how they solved
the problems. For Question 6, students explain how
to finish solving a problem, and for Question 7, students
determine whether or not a problem was
solved correctly. See Sample Dialog 2 for a discussion
of these two problems.

Use the sample dialog to guide your discussion of Questions
6–7 on the Animal Trading Cards pages in the Student
Activity Book.
Teacher: How would you help Nicholas find the answer for
Question 6? What do you think of the way he started
to solve the problem?
Miguel: I think he started the problem the right way because
the problem said that Kim had 17¢ and he started at 17
on the number line. She had a dime left over, so
Nicholas found 10 on the number line. I think the next
step is to count back from 17 to 10 to see how much
Kim spent: 16, 15, 14, 13, 12, 11, 10 [holding up one
finger for each number]. There are 7 numbers between
10 and 17. She bought a lion card.
Sarah: I did it a different way. I found 10 on the number line
and drew a line from 0 to 10 to show how much she
had left. Then I drew a line from 10 to 17 for the card
she bought. I counted up from 10 to 17: 11, 12, 13, 14,
15, 16, 17. The answer is 7. That's a lion card.
Faith: I used ten. I know that 10 + 7 = 17, so Kim spent 7¢
on a card.
Teacher: Those are excellent ways of solving the problem!
Now let's look at Question 7. Did Emily solve the
problem correctly?
Sam: The ant card costs 8¢. When Emily counted back, she
started at 13 and she should have started at 12 because
that's one back from 13. She counted the numbers
instead of the spaces. She should have counted: 12, 11,
10, 9, 8, 7, 6, 5. She has 5¢ left and she can buy a
whale card.
Fern: I used the part-whole diagram. I know that Nisha had
13¢ and that goes in the "whole" box. She bought an
ant card that costs 8¢ and that goes in one of the "part"
boxes. To find the other part, I counted up from 8 until I
got to 13: 9, 10, 11, 12, 13. She has 5¢ left and she can
buy a whale card.
Teacher: Good thinking, Sam and Fern! Remember to
make sure you use an efficient strategy that is quick
and accurate. When you show your work, you can see
what you did if you make an error.

It is important that students represent addition and subtraction
on tools and explain their reasoning. Strategies and tools
that students are learning with smaller numbers will be
extended to operations with multidigit numbers in later units.
Students who are already fluent with single-digit addition and
subtraction should still take time to represent the operations
on the number line or other tools so they become familiar
with these representations.
For students who are still developing efficient strategies for
addition and subtraction facts, the number line, ten frame,
and part-whole diagram serve as powerful tools to support
student reasoning. Encourage these students to develop representations
that make sense to them and that will help them
visualize their reasoning about numbers and operations.

The animal group names are used on the trading cards, but
they are not used in the problems. The word problems refer
only to the names of the animals (e.g., whale and monkey).
Language learners can match the animal names in the problems
to the pictures on the cards.
Students who are interested in learning more about animal
group names can read A Cache of Jewels and Other
Collective Nouns by Ruth Heller.
Encourage students to use the tools to support their
counting and reasoning strategies as they find the
solutions. Remind students to use the Math
Practices page to guide them as they solve the problems.
Upon completion, choose one or two problems to
discuss as a class.
- What is the question? What words and numbers
do you need to answer the question?
- Did you choose good tools and an efficient strategy?
- How did you show your work?
- What strategies might you use?