Lesson 6

Use Doubles

Est. Class Sessions: 2

Developing the Lesson

Part 1: Think about Doubling

Read Two of Everything. Show students the cover of the Two of Everything book by Lily Toy Hong.

Ask:

X
  • What do you think this story is about? (Possible responses: a grandma and grandpa, two eyes, two ears, two birds, two hills)
  • What are some things that you have two of? (Possible response: two shoes, two hands, two feet, two eyes, two knees)

Read the story aloud pausing to emphasize the changes in the story and answer students' questions.

Once you are done reading, ask:

X
  • What is your favorite part?

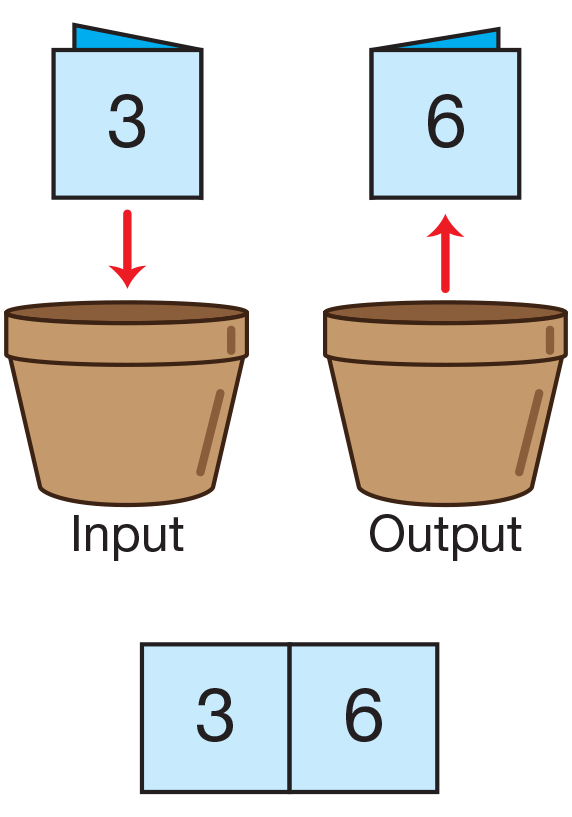
Build a Doubles Rule Machine. Show students the magic pot you prepared. Tell students to pretend that this pot is a magic pot. Place a train of 3 connecting cubes in the pot. Pull a train of 6 six connecting cubes out of the pot. Fold one of the rule machine rows you prepared in half. Write 3 on the left side or "input" side and 6 on the right side or "output" side. Show students the 3 and place it in the pot.

Ask:

X
  • What will happen to the three when I put it in the magic pot? (Possible response: The number will double.)
  • What is the double of 3? (six)

Remove the rule machine row showing students the 6. Hang the row on the board to make a rule machine. See Figure 2. Repeat this simulation with 4 cubes. Tell students that it is their turn to try. Give each student one of the rule machine rows you prepared showing an input that they will double. See Materials Preparation. Have 20 connecting cubes available for each student.

As students are doubling the input on their row, ask them to record the double on the right side of their row. Observe students' strategies for finding doubles and choose a few students to share their strategies. As students complete their rows, ask them to add them to the rule machine you have already started.

X

When building and analyzing patterns in tables and rule machines, students often have trouble focusing on the relationship between the input and the output. By breaking the table into rows, students are forced to focus on this relationship rather than the relationship between the rows.

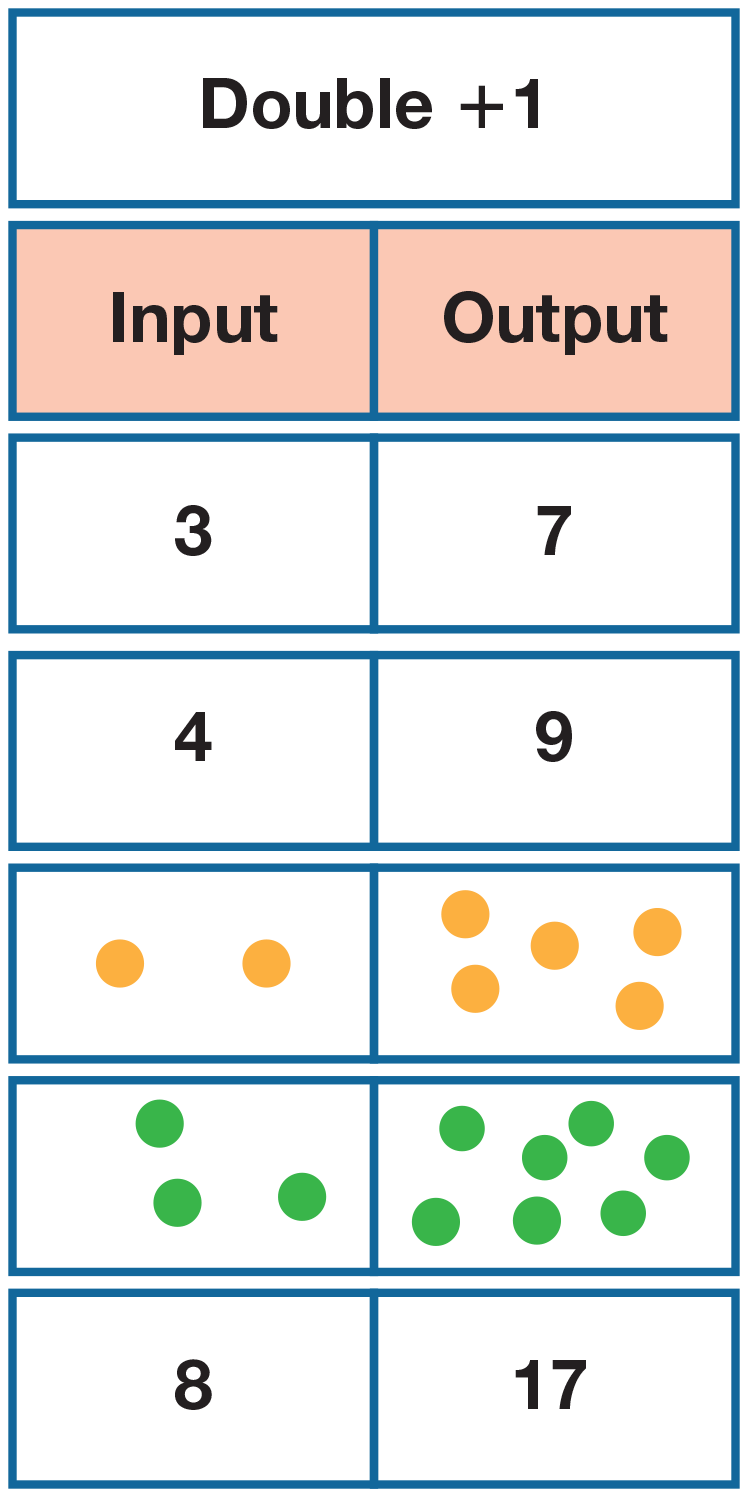
Build a Doubles +1 Rule Machine. Tell students that you found another magic pot. Gather the doubles +1 rule machine rows you prepared. See Figure 3. Fold the first row so only the 3 is showing. Without telling students the rule of the pot, place the row into the pot and remove it showing only the 7.

Ask:

X
  • What magic does this magic pot perform on numbers? What happened to the 3 to get 7? (Possible response: 4 more; double +1)

Display the row on the board beneath an input/output title. Fold the second row so only the 4 is showing. Place the row into the pot and remove it showing only the 9.

Ask:

X
  • What magic does the magic pot perform on numbers? What happened to the 4 to get 9? (Possible response: add 5; double +1)
  • Could the magic be "add 5?" (Possible response: no because the pot did not add 5 to 3 to get 7. The pot needs to do the same thing each time.)

Display the row on the board as before. See Figure 6. Fold the next row so the 2 dots are showing. Place the row into the pot and remove it showing only the 5 dots. Display the row on the board with the others. Give each student one of the rows you prepared. Tell students to find the output using the input shown on the row. If they are not sure of the rule of the magic pot, tell them to wait until other students have displayed their rows on the rule machine on the board. As students complete their rows, ask each student to add his or her row to the rule machine.

Ask:

X
  • What is the rule of the magic pot? (Possible response: It is doubling the number and adding one.)
  • Look at the all the data from the magic pot. Do all the output numbers show this rule?

Write "Double +1" rule above the rule machine.

Adventure Book:
Student Activity Book:
Master:
Using a "pot" to simulate doubling
X
+
Rule machine for Double +1
X
+