Lesson 7

Subtraction Strategies Seminar

Est. Class Sessions: 2

Developing the Lesson

Part 1: Building a Subtraction Strategies Menu

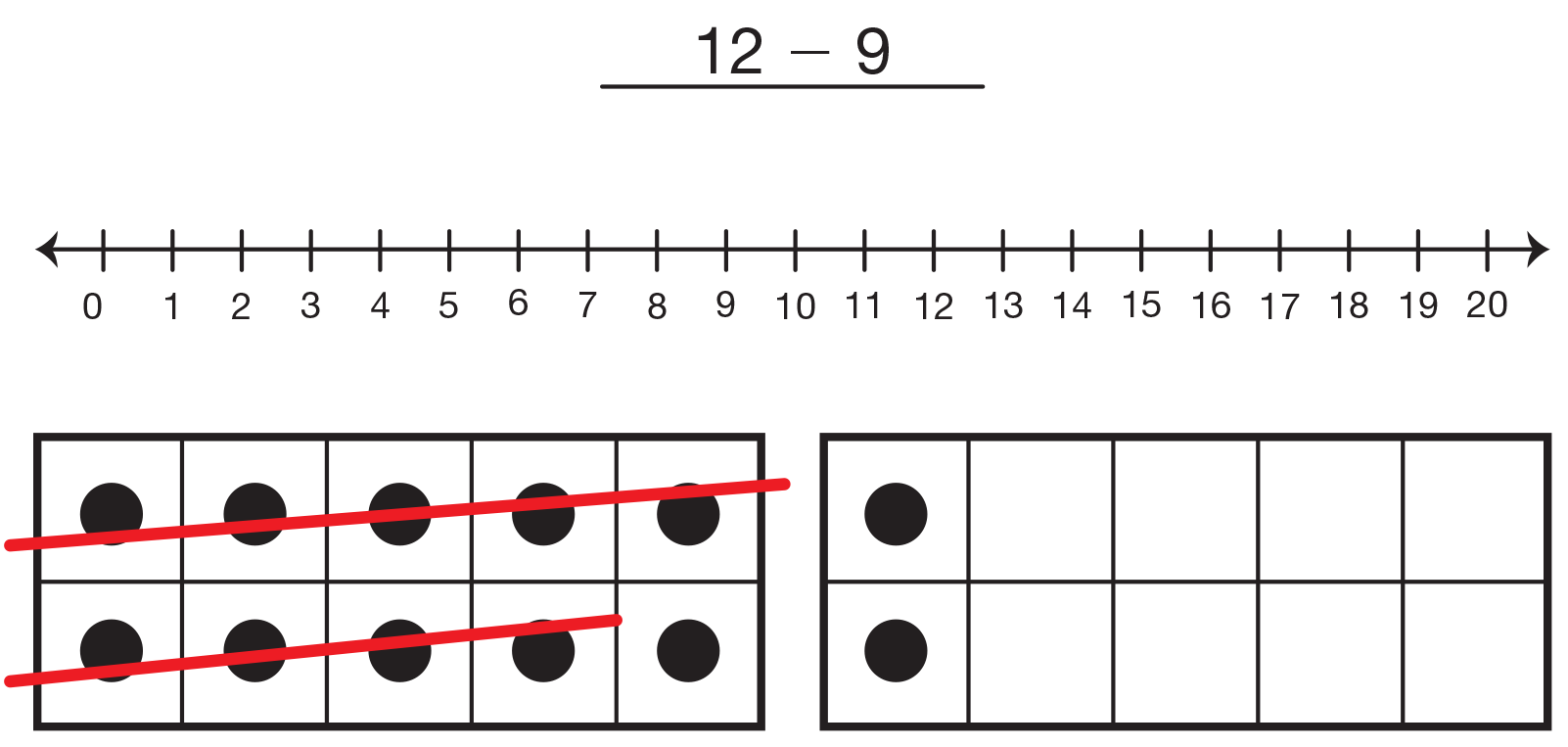
Describe Strategies for Subtraction Facts. Tell students they are going to have a "strategy session" about subtraction similar to the one they had for addition in Lesson 3. Explain that they will solve problems within 20 and pay special attention to the strategies they use. Display the two sheets of chart paper and the Show Your Strategy Cards with the facts 12 − 9, 16 − 7, 8 − 6, 5 − 3, and 14 − 6. See Materials Preparation. Focus students' attention on the displayed cards and ask students to explain how to solve each problem.

Ask:

X
  • Look at the subtraction facts on the five Show Your Strategy Cards. Who would like to show the class how to solve 12 – 9?
  • Describe your strategy. (Possible response: I know that 12 − 10 is 2, so 12 − 9 is 3 because you're taking away 1 less.)
  • What tools did you use to solve the problem? (Possible response: I used the ten frames.)
  • Describe how you used the tool to solve the problem. (Possible response: I filled up 2 ten frames with 10 dots on the first one and 2 dots on the second one. Then I knew that 9 is one less than a whole ten frame, so I left one on the first ten frame and added it to the 2 on the second ten frame. That makes 3.)

As students describe their thinking, ask them to show their thinking using the tools and space on the Show Your Strategy Cards Display Master. Have connecting cubes readily available as well. Then record that solution on the corresponding card you prepared. See Figure 3. Repeat this discussion for the other four facts displayed.

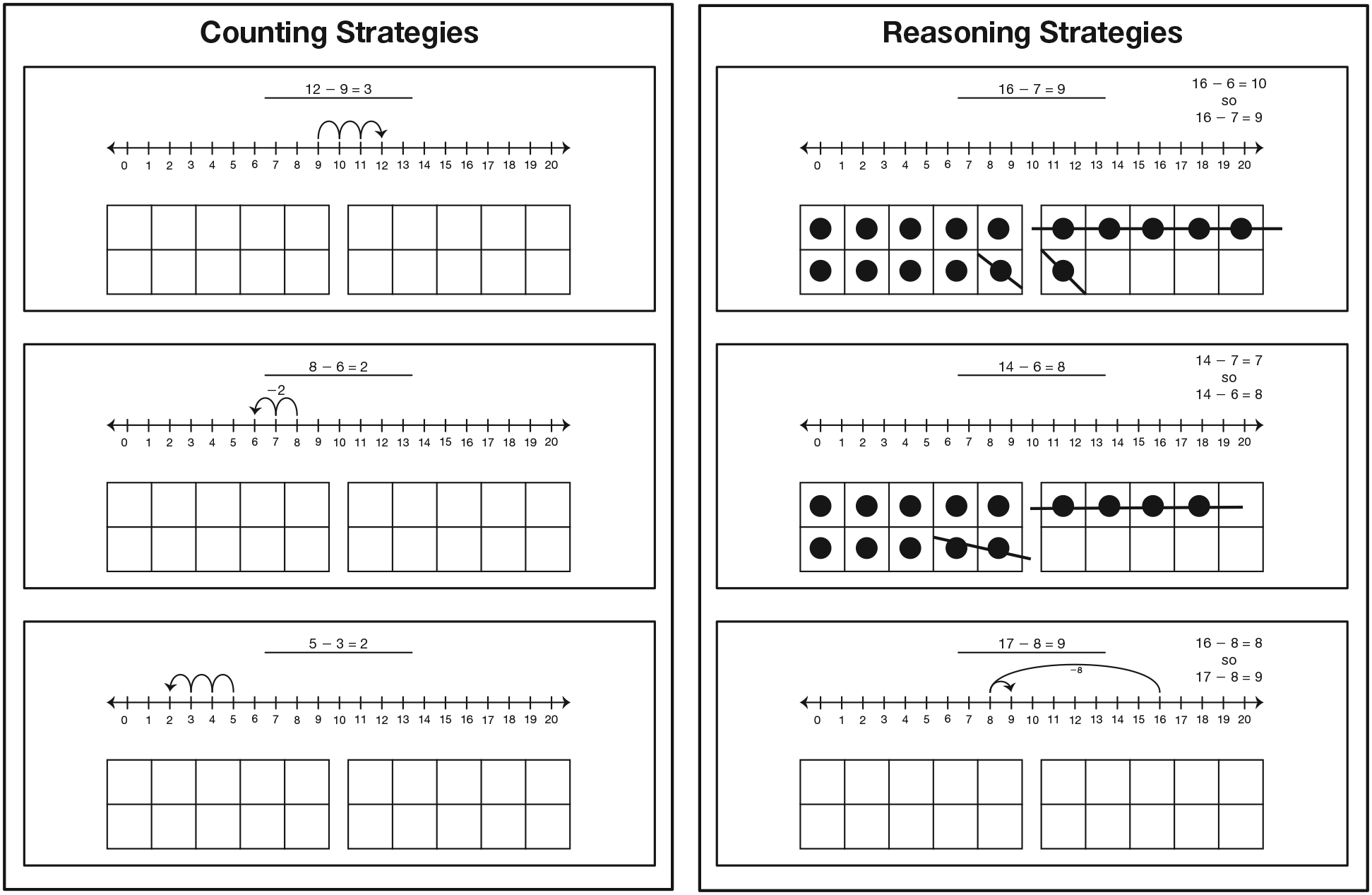
Introduce the Counting Strategies and the Reasoning Strategies charts.

Ask:

X
  • Now look at the 2 charts: Counting Strategies and Reasoning Strategies.
  • Who can explain what counting strategies are? (Possible response: Counting strategies are when you count to find the answer. For counting up, I start with the smaller number and count up to the larger number. For counting back, I start with the larger number and count back the smaller number.)
  • Who can explain what reasoning strategies are? (Possible response: Reasoning strategies are strategies that use what you already know to help you solve the problem like using doubles and making tens.)
  • Where would you place the fact 12 − 9? (Possible response: I would put it on the Reasoning Strategies chart because we can use ten to figure out the answer: 12 − 10 = 2, so 12 − 9 = 3.)

Post the Show Your Strategy Card on the appropriate chart. See Figure 4. Ask:

X
  • When would you use a counting strategy and when would you use a reasoning strategy? (Possible response: You can use a counting strategy to count up or count back small numbers like 1, 2, or 3. If you have larger numbers, try to use what you know to solve the problem.)

Encourage students to use efficient strategies. See the Sample Dialog to guide your discussion of subtraction strategies.

X

Use this Sample Dialog to guide your discussion of subtraction strategies.

Teacher: What strategy did you use to solve 12 − 9?

Maria: I counted on my fingers to 12: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12. Then I took away 9 fingers and that left 3.

Teacher: Maria used a counting strategy. Do you think it's efficient to count up to 12 and count the 9 you took away?

Tara: You don't have to count up to 12 because you know that's the number you start with. I used the strategy using ten. I know that 12 − 10 = 2, so 12 − 9 is 3 because you take away one less.

Teacher: Good thinking, Tara! We should try to use strategies that are fast and accurate. Did you use a counting strategy or a reasoning strategy?

Tara: It's a reasoning strategy.

Teacher: Okay, let's put our strategy card on the Reasoning Strategies chart. Who can tell me how you solved 16 − 7?

Chris: I know that 7 + 9 = 16, so 16 − 7 = 9.

Teacher: Great! Chris used his knowledge of fact families to solve the problem. On which chart should we place the strategy card?

Chris: We should place it on the Reasoning Strategies chart because I used what I know to solve the problem.

Teacher: What strategy did you use to solve 8 − 6?

Josh: I used counting up. I put 6 in my head and counted up to 8: 7, 8. The answer is 2.

Teacher: I like your thinking. You put 6 in your head instead of counting up to 6. Where would you place the strategy card?

Josh: Since I counted up, I would place it on the Counting Strategies chart.

Teacher: Good answer! How did you solve 5 − 3?

Javier: I used the number line. I started at 5 and went back 3 hops. My answer is 2.

Teacher: That's another strategy. On which chart would you put the card?

Javier: I would put it on the Counting Strategies chart because I counted back. I could have used counting up, too, if I started at 3 and counted up to 5.

Teacher: So, Javier just told us that sometimes you could use more than one strategy to solve a problem. How did you solve 14 − 6?

Rachel: I used doubles. I know that 14 − 7 = 7, so 14 − 6 is one more or 8.

Teacher: Excellent, Rachel! Where would you place the strategy card?

Rachel: It goes on the Reasoning Strategies chart because I used what I know to solve it.

X

Naming Strategies. There are many different ways to name a strategy. Encourage students to use names that are meaningful and will help them remember the strategy. Names can be related to the steps in the strategy, like "counting back" or "counting up." Names can also be selected because students assciate the strategy with a particular student in the class who regularly uses a strategy. It is not important that students be able to name the strategy, though it does help them discuss and distinguish them.

Next have students focus their attention on the Show Your Strategy Cards with the subtraction fact 16 – 7.

Ask:

X
  • What strategy would you use to solve 16 − 7? (Possible response: I used fact families.)
  • Describe your strategy. (Possible response: I know that 7 + 9 = 16, so 16 − 7 = 9. They're all in the same fact family.)
  • Is your strategy a counting strategy or a reasoning strategy? Why? (Possible response: It's a reasoning strategy because I'm using what I know about fact families to solve it.)
  • Are there other strategies you can use to solve this problem? (Possible response: Yes, I can also use doubles. I know that 16 − 8 = 8, so 16 − 7 = 9.)

Follow the same procedure for the remaining cards: 8 – 6, 5 – 3, and 14 – 6 and place the cards on the appropriate charts. Encourage students to use different strategies and tools to solve the remaining problems on the strategy cards.

Sort Subtraction Facts on Show Your Strategy Cards. Have students work in groups to discuss strategies for the remaining subtraction facts you prepared on the Show Your Strategy Cards. Give 4–5 facts to each group. As they finish, you may give them additional facts to solve. Ask each group to solve the subtraction facts and show their strategy with the number line, ten frames, a drawing, or with number sentences. As groups complete their cards, have them attach the cards to the chart that corresponds to the strategy that they used to solve the problem.

Ask:

X
  • What strategy did you use?
  • What tools did you use to solve the problem? (number lines, connecting cubes, ten frames)
  • Should you place your card on the Counting Strategies or Reasoning Strategies chart?

Some students may have trouble naming their strategy. Allow students to place their card on the chart they think is appropriate. If they do not choose the appropriate chart, there will be a chance to rearrange the cards later.

X

There are 72 subtraction facts grouped by strategy in the Subtraction Facts chart. Start by giving each student group 4–5 Show Your Strategy Cards from different groups on the chart. Encourage students to use a variety of strategies and to think about when it is appropriate to use counting strategies and reasoning strategies. As students finish working on their strategy cards, give them additional cards. Depending on the size of your class, you may not use all 72 cards.

Discuss Counting and Reasoning Strategies. Upon completion, direct students' attention to the subtraction facts on the Counting Strategies and Reasoning Strategies charts.

Ask:

X
  • When does it make sense to use a counting strategy? (Possible response: When you are counting up or counting back a small number like 1, 2, or 3.)
  • Does it make sense to use counting to solve all the facts we placed on the Counting Strategies chart? (Possible response: No, we want to use a strategy that is quick and accurate. We don't want to use counting strategies to subtract large numbers.)
  • Are there facts that you would like to move from this chart to the other chart? Why?

Students may want to move some of the facts to the Reasoning Strategies chart. Direct students' attention to the facts on the Reasoning Strategies chart. Have a few students share their reasoning strategies.

Ask:

X
  • What strategy did you use to solve [12 − 6]? (Possible response: I know that 6 + 6 = 12, so 12 − 6 is 6.)
  • Did anyone else use this strategy to solve a different subtraction fact?
  • What are some of the reasoning strategies you used? (using ten, using doubles, making ten, thinking addition)
  • Can you use more than one strategy for some of these facts? (Possible response: For 13 − 9, you can use the using-ten strategy. I know 13 − 10 = 3, so 13 − 9 = 4. I could also count up. I put 9 in my head and count up to 13. The answer is 4.)
X

Students have been inventing and using counting strategies to solve problems using subtraction throughout First Grade. In this lesson, students will focus on deciding which strategy is more efficient for a given problem. Students will also explore reasoning strategies (doubles, using ten, using doubles, making ten). This lesson provides practice and attention to the counting and reasoning strategies.

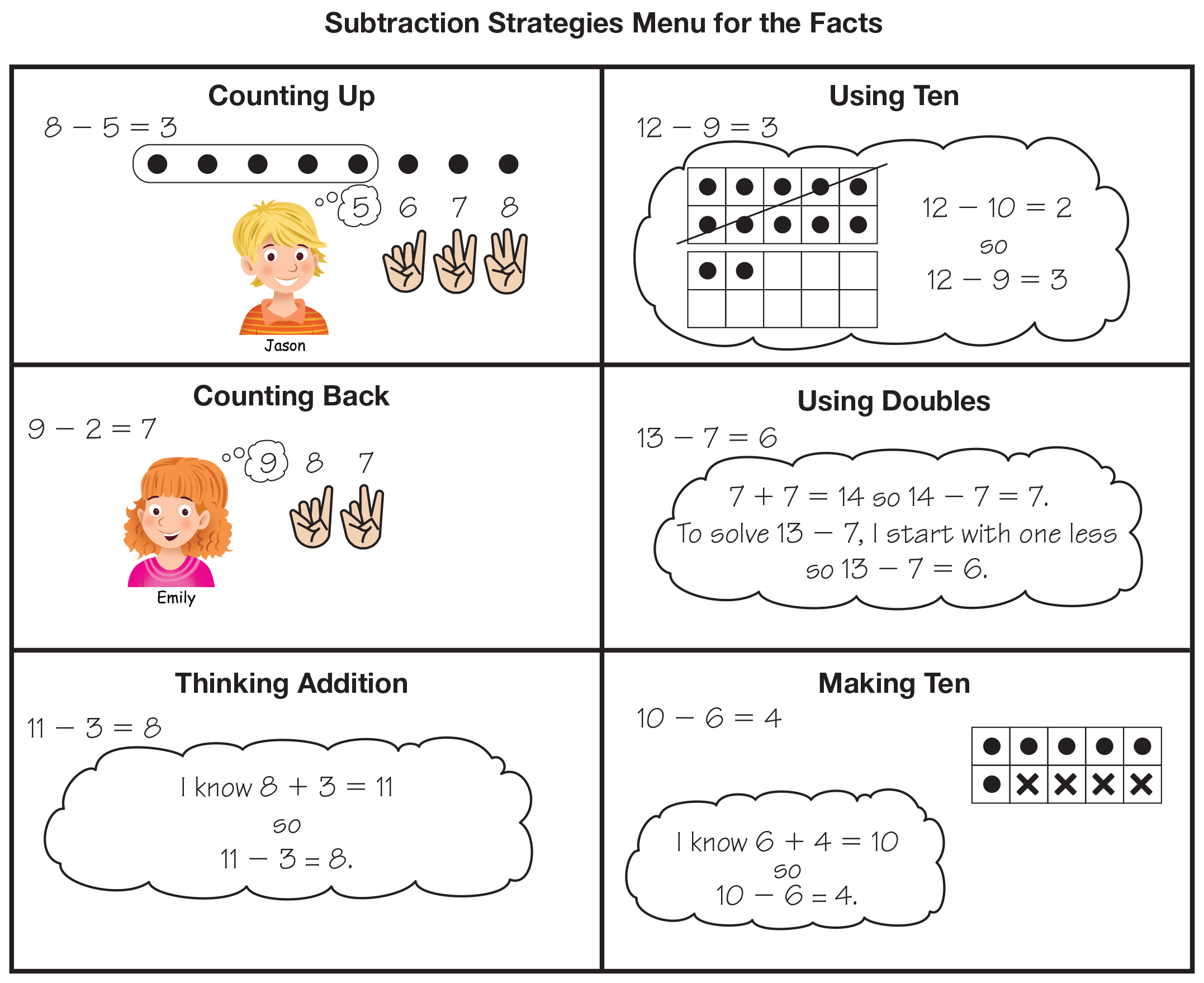
Compare to Subtraction Strategies Menu. Display and ask students to refer to the Subtraction Strategies Menu for the Facts in the Student Activity Book. See Figure 5. Ask students to compare the Subtraction Strategies Menu for the Facts to the strategies they collected on the charts.

Ask:

X
  • What is the same?
  • What is different?
  • Are there any strategies that you would like to add or change? (Possible response: Subtracting zero is a reasoning strategy that is not on the chart. Subtracting zero is a reasoning strategy because we know that subtracting zero doesn't change the number.)
  • Are there strategies on the menu that were not on our charts?

Have students add other strategies they think of to the back of the menu.

Adventure Book:
Student Activity Book:
Master: SYS
X
SG_Mini
+
Using ten frames to solve 12 − 9
X
+
Sample charts showing subtraction facts sorted by strategy
X
+
Subtraction Strategies Menu for the Facts from the Student Activity Book
X
+