The Meaning of the Mean

Est. Class Sessions: 2–3

Developing the Lesson

Part 1. Finding the Mean Head Circumference

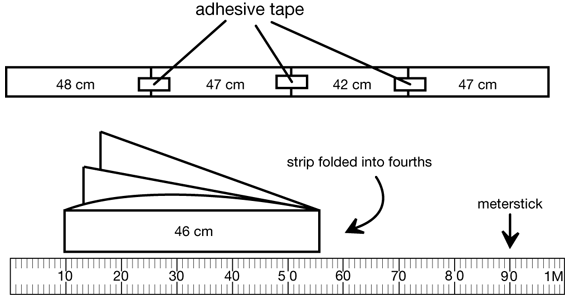
Measure with Adding Machine Tape. Students work on this activity in groups of four. (See TIMS Tip below.) Students begin the activity by reading The Meaning of the Mean pages in the Student Guide and following the directions. Groups measure the head circumference of each member using adding machine tape and record the measurements in a data table for the group. For each student, a strip of adding machine tape is cut the same length as his or her head circumference.

Before students begin, you may wish to demonstrate a procedure for cutting the strips safely. One student should wrap the adding machine tape around his or her partner's head and mark with a crayon the spot where the tape overlaps. Then, after removing the adding machine tape from the student's head, cut the strip at the crayon mark and measure it to the nearest centimeter. Students can check to see that they have measured accurately by wrapping the tape around the head again. If the ends of the tape just touch one another, the tape is the same length as the circumference of the head.

To find the average head circumference of students in a group, the group tapes their strips together, taking care not to let the ends overlap. Then, the group folds this long strip into as many equal parts as there are students in the group. See Figure 1. The length of each of these parts is the mean head circumference for the group. Each group should record the mean circumference at the bottom of their data table.

Groups of Four. Since it is easy to fold the strip into fourths, four students per group is a good choice. If the number of students in your class is not divisible by four, you will have to make some groups of three. You may need to help these groups fold their long strips since folding into thirds is trickier than folding into fourths.

This process of taping the strips together and then folding the long strip in equal parts models the procedure for finding the mean. In the previous activity students “evened out” the heights of the towers of connecting cubes. Here students “even out” the length of the strips. To find the mean numerically, we add up the values and divide by the number of values. This is similar to taping the strips together and then folding the strip into equal parts.

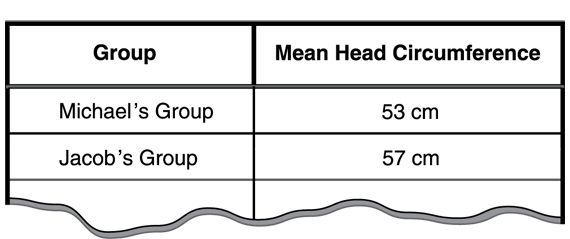
Responsiveness to Students. Some students may be sensitive about sharing data about their physical attributes with the class, particularly if their head circumference is relatively large or small compared to others. Avoid reporting individual data to the whole class. Instead, focus the whole-class discussion on averages of the groups and of the whole class.

Estimate the Mean Head Circumference for the Class. Discussing Questions 1–3 on The Meaning of the Mean pages in the Student Guide will give you an opportunity to check students' understanding of the meaning of the mean. Each group should add their group's mean to a class data table on chart paper or using a display of Two-Column Data Table. See Figure 2. These questions ask students to estimate the mean circumference for the entire class using the group means. During one class discussion, a student said that the mean should be a number “in the middle,” not at the ends. This showed a good understanding of the concept.