To set the stage for the activity, read the story of Irma and Luis on the Function Machines pages in the Student Guide.
The concept of a function is an important one. Your students will study it formally when they study algebra in middle school or high school. One way to define a function is to say that it is a rule that assigns to every input number exactly one number, the output number. For example, every time your input is five, you get the same output. (A mathematical definition of function is more precise, but is not necessary at this level.) Functions can be described in many different ways: in words (e.g., the “squaring function”), in symbols (e.g., the squaring function can be written y = x2), in data tables, and in graphs.
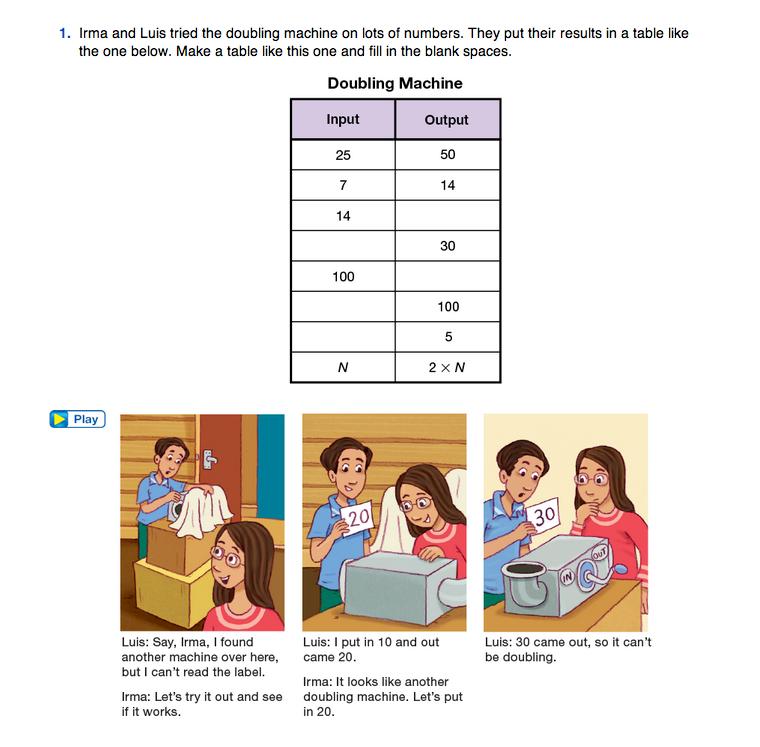
Question 1 encourages students to explore doubles with the Doubling Machine. Use a display of the Two-Column Data Table Master to organize the information. Label the columns of the data table Input and Output. Complete the data table by having students tell you certain numbers to double, then record what the machine would do. A sample data table for the Doubling Machine is shown in Figure 1. Note that the first blank entry asks for the output when the input is 14.
On the next line the output is 30 and we are asked for the input.
- What is the number whose double is 30? (Some students may require trial and error to find the answer to this problem, while others will see that the input number must be half of the output number.)
For large numbers, students can use their calculators to find the output.
- If 673 is the input, then what is the output? Note that there is more than one way to do this on a calculator. Students might add 673 + 673 or they might multiply by 2: 2 × 673.)
Continue the Student Guide vignette leading to an exploration of the Add 10 Function Machine in Questions 2–4.
Use a display of the Two-Column Data Table Master to display the table in Question 2.
- Look at the numbers in the table. What patterns do you see? (The output for each number is 10 more than the input.)
- Look at the number 45 in the output column. What do you need to do to find the input? Explain how you know. (You will need to subtract 10 from 45. If you add 10 to get the output for a number you would have to subtract 10 from the output to go back to what the number was before it went through the machine. That is like undoing the machine.)
Ask students to complete the table and then use Questions 3–4 to discuss how to describe the function machine in words and using symbols. Write the rule for this machine in the last space in the output column.
Questions 5 and 6 model how students can examine patterns in a table and test possible rules. Use these opportunities to help students find the relationship between the input and output numbers in each function table. Ask students to look at the table in Question 5. The sample dialog offers some guiding questions to start Question 5.

Use this Sample Dialog to guide discussion of Question 5 in the Student Guide.
Teacher: Let's look for a pattern in the table in Question 5. What are the ways to get from 1 to 3?
Jimmy: I could add 2. 1 + 2 = 3
Sharon: I could multiply 1 by 3. Maya: I could multiply by 2 and add 1. Teacher: Any others?
Lily: I think the rule is add 4 because 2 + 4 is 6 [referring to the second row in the table].
Teacher: Well, which rule works? Test your rule.
[Students work for a few minutes.]
Lily: My rule does not work.
Teacher: Why do you think that?
Lily: Because 1 + 4 is not 3 and 5 + 4 does not equal 15. The rule has to work for everything.
Jimmy: Mine doesn't work either. It does not work for everything. It only works for the first row.
Sharon: Mine seems to work. 2 × 3 = 6, 5 × 3 = 15.
Teacher: Let's all choose a different input and see if Sharon's rule works. Does N × 3 work for everything?
Students: Yes!