Lesson 1

Invented Strategies

Est. Class Sessions: 2–3

Developing the Lesson

Part 1: Developing Strategies for Problems with Sums to Twenty

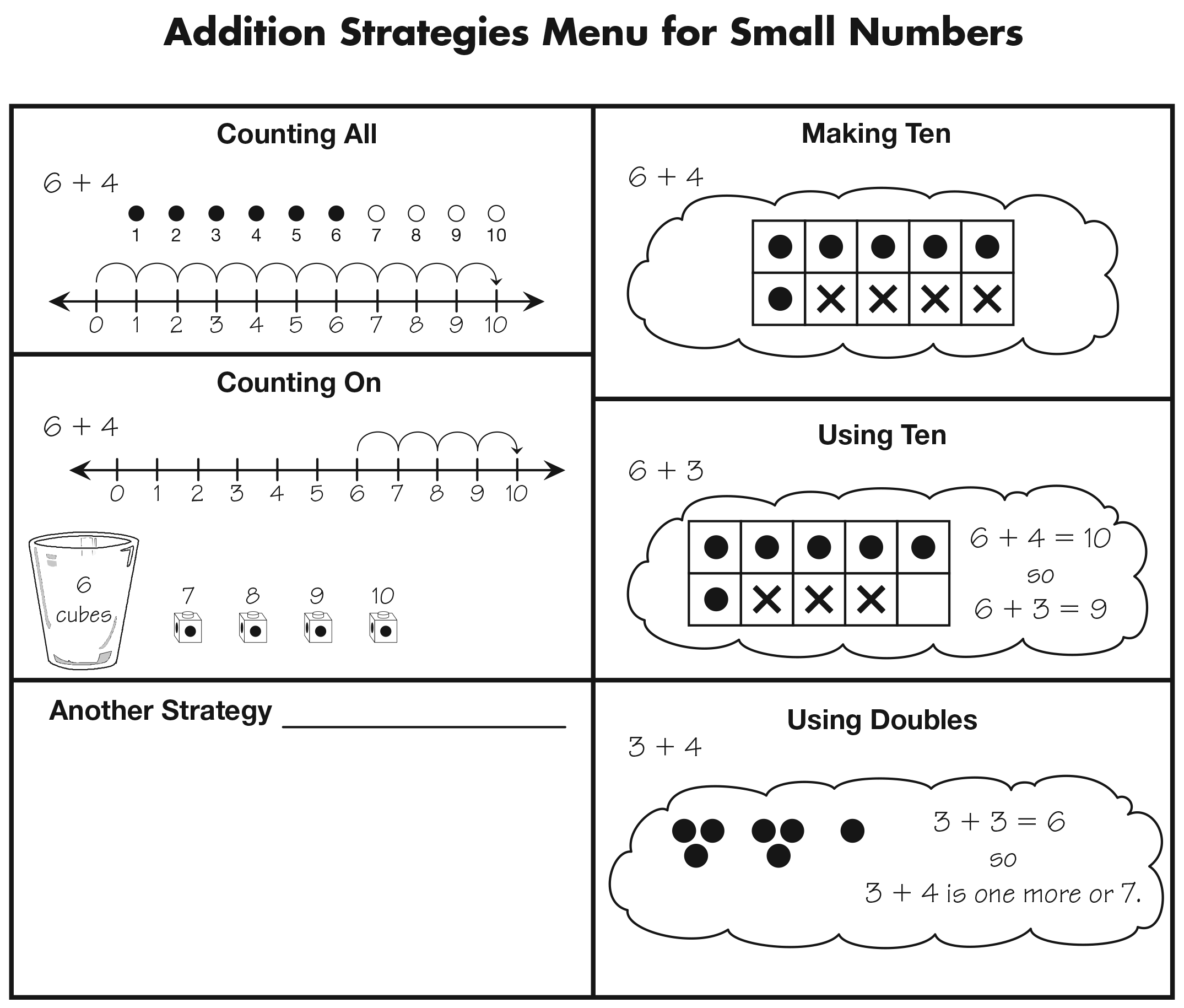
Review Addition Strategies. Begin the lesson by reviewing some of the strategy work from Unit 6. Tell students that today's work will be called a "strategy session." They will solve different types of problems with sums greater than 10 and pay special attention to the strategies they use. Use the display of the Addition Strategies Menu for Small Numbers made in Unit 6 and in the Student Activity Book Reference section to review the strategies. See Figure 2.

Say:

X
  • Look at the strategies on the Addition Strategies Menu for Small Numbers. What are some of the strategies you can use to add numbers? (counting all, counting on, making ten, using ten, using doubles)
  • Look at the problem on the chart. I want you to solve the problem using some of the strategies on the Addition Strategies Menu for Small Numbers. Also, think of other strategies you can use to solve this problem.

Display the sample problem you prepared and ask students to brainstorm as many strategies as possible that they can use to solve the problem. See Materials Preparation. Allow time for students to solve the problem. Have number lines, 100 Charts, ten frames, and connecting cubes available for students to use.

Use Tools and Strategies to Solve Problems. When students are finished working on the sample problem, have them describe their strategies and decide which ones are most efficient.

Ask:

X
  • What strategies or tools did you use to solve the problem? (counting all, counting on, or modeling with connecting cubes, fingers, ten frames, or number line)
  • When you choose a strategy, think about whether or not it is an efficient strategy—one that is quick and accurate. For example, it's not efficient to use counting on to add 17 + 19. Why not? (Possible responses: It takes too long to count on 19. It's hard to use your fingers and to keep track.)
  • Is it efficient to use the strategy counting all when you have larger numbers? (Possible response: No, because you should start from one of the numbers and count on or use a different strategy.)
  • When would you use the strategy counting on? (Possible response: when you add 1, 2, or 3)
  • When would you use the strategy using ten? (Possible response: when you're adding numbers that are close to facts for 10)
  • When would you use the strategy using doubles? (Possible response: when you're adding numbers that are close to a doubles fact)

Allow students to describe any of the strategies in their own words. Encourage students to articulate the strategy rather than simply identify the strategy.

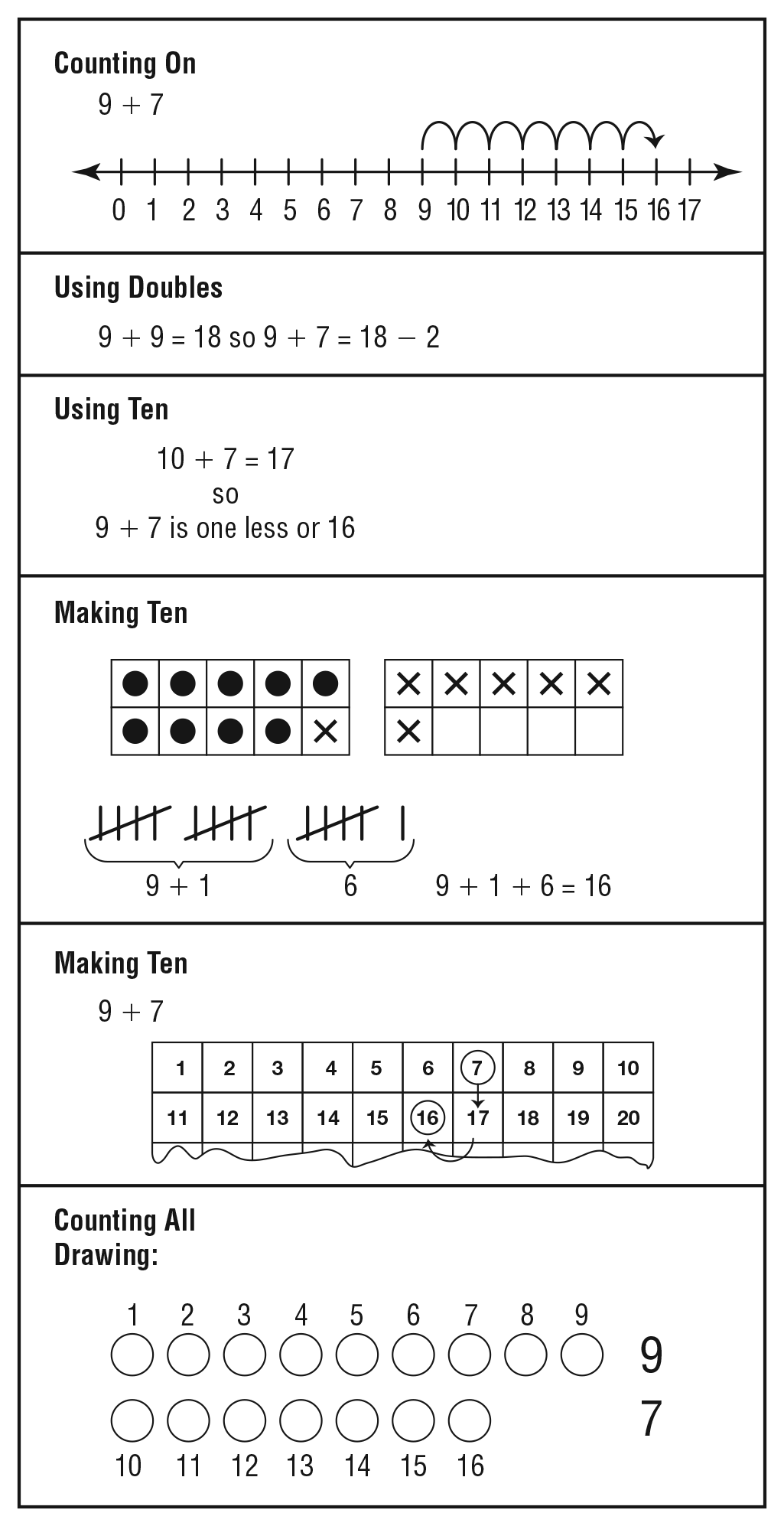
Write the title "Invented Strategies" on a chart and list the different strategies students use to solve the problem. See Figure 3 for a sample strategy chart. During the unit, add additional strategies as students come up with new strategies for solving problems with sums larger than 10. Ask a student to choose a strategy and explain it to the class.

Ask:

X
  • Who can show the same strategy in a different way, with a different diagram or drawing?

Encourage students to recognize that for any one problem there may be several different strategies for solving it. With each strategy, there may be several different ways to draw or represent it in a diagram or picture. The Sample Dialog gives an example of a class discussion about strategies.

X

Use this sample dialog as an example for using invented strategies.

Teacher: Who would like to show us your strategy for solving this problem?

Jacob: I counted on. I added 9 + 7. I started with 9 and put up 7 fingers. I counted 9, 10, 11, 12, 13, 14, 15. The answer is 15.

Teacher: What does everyone else think?

Aaron: I don’t think that counting on is an efficient strategy because both numbers are large. Also, I think Jacob should have put 9 in his head and started counting 10, 11, 12, 13, 14, 15, 16. I used connecting cubes, and I got 16. First I put together a train of 9 cubes and a train of 7 cubes. To count them, I took one cube from the 7 cubes and put it on the 9 cubes and that made 10. Then I had a train of 10 cubes and a train of 6 cubes.
I added 10 + 6 = 16.

Teacher: That was a great strategy! Aaron made a train of 10 and that made it easier for him to count the cubes. Did anyone solve the problem in a different way?

Maya: I got the same answer but I used a ten frame. I started with 9 on one ten frame. I took 1 from the 7 to fill up the first ten frame. Then I had 10 on one ten frame and 6 on the other. That makes 16.

Teacher: Maya and Aaron both used the strategy of making a 10 but Maya used a ten frame and Aaron used connecting cubes. Who has a different strategy?

Nila: I drew tally marks. First I made 9 tally marks and then I added one more to make 10 and I kept adding 6 more tally marks. I counted by fives 5, 10, 15, and one more makes 16.

Teacher: That’s interesting, Nila. What do you think of her strategy?

Gwen: I think tally marks are better than drawing one line for each number because you group them in fives, but when you have real large numbers it’s hard to use tally marks.

Teacher: Good thinking, Gwen! Remember that for Math Practice 2, we know we want to use efficient strategies that are quick and accurate. Does anyone else have a different strategy?

Joey: I used the 100 Chart. I know that to add 10, you go straight down one row, but I’m adding 9. I started with 7 and moved straight down one row and back 1. I got 16.

Teacher: We’re coming up with a lot of strategies! Who has a different strategy?

Jason: I drew 9 circles and 7 circles. I counted 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16.

Teacher: Jason got the right answer, but let’s think about it. If you draw one circle to represent each number, is that an efficient strategy for this problem?

Kara: I don’t think so because when you get to larger numbers, you don’t want to make one circle for each number you’re counting. Also, you don’t have to start counting from 1 because you counted the 9 circles when you drew them, so you just count on.

Teacher: Good answer! What other strategies did you use to solve this problem?

Nick: I used doubles. I know that 9 + 9 is 18, so 9 + 7 is 2 less or 16.

Teacher: Great job, everyone! We have several different strategies. Let’s write the strategies on our Invented Strategies chart. If we think of other strategies, we can add them to the chart.

Practice Invented Strategies. Have students work in pairs to complete the Use Strategies to Solve Problems pages in the Student Activity Book. Display the corresponding display to model how to write or show the strategy. Refer to the display of the Math Practices page from the Student Activity Book Reference section. Explain to students that they should use the following Math Practices as they solve the problems:

  • MPE1. Know the problem. I read the problem carefully. I know the questions to answer and what information is important.
  • MPE2. Find a strategy. I choose good tools and an efficient strategy for solving the problem.
  • MPE3. Check for reasonableness. I look back at my solution to see if my answer makes sense. If it does not, I try again.
  • MPE5. Show my work. I show or tell how I arrived at my answer so someone else can understand my thinking.

X

Make clear to students that they can use stick figures or Xs to represent the problem and that a "lifelike" representation is not necessary.

Remind students to use connecting cubes, ten frames, 100 Charts, and number lines. When they complete the problems, go through each problem and have students demonstrate how they solved the problems. Add new strategies to the Invented Strategies chart.

Student Guide:
Student Activity Book: 361 362
Answers
X
SAB_Mini
+
X
SAB_Mini
+
Master:
Addition Strategies Menu for Small Numbers made in Unit 6
X
+
Sample Invented Strategies chart
X
+