Lesson 6

Thinking about Number Sentences

Est. Class Sessions: 2

Developing the Lesson

Part 2: Finding Missing Numbers

Display the following set of four number sentences:

  1. 4 + 5 = 5 + 4
  2. 4 + 4 + 1 = 8 + 1
  3. 4 + 4 + 1 = 1 + 4 + 4
  4. 5 + 4 = 9 − 0

Ask:

X
  • Which of these number sentences are true? Work with a partner to find out. Be prepared to share what tools helped you decide. (All of them are true.)

Next, display the following:
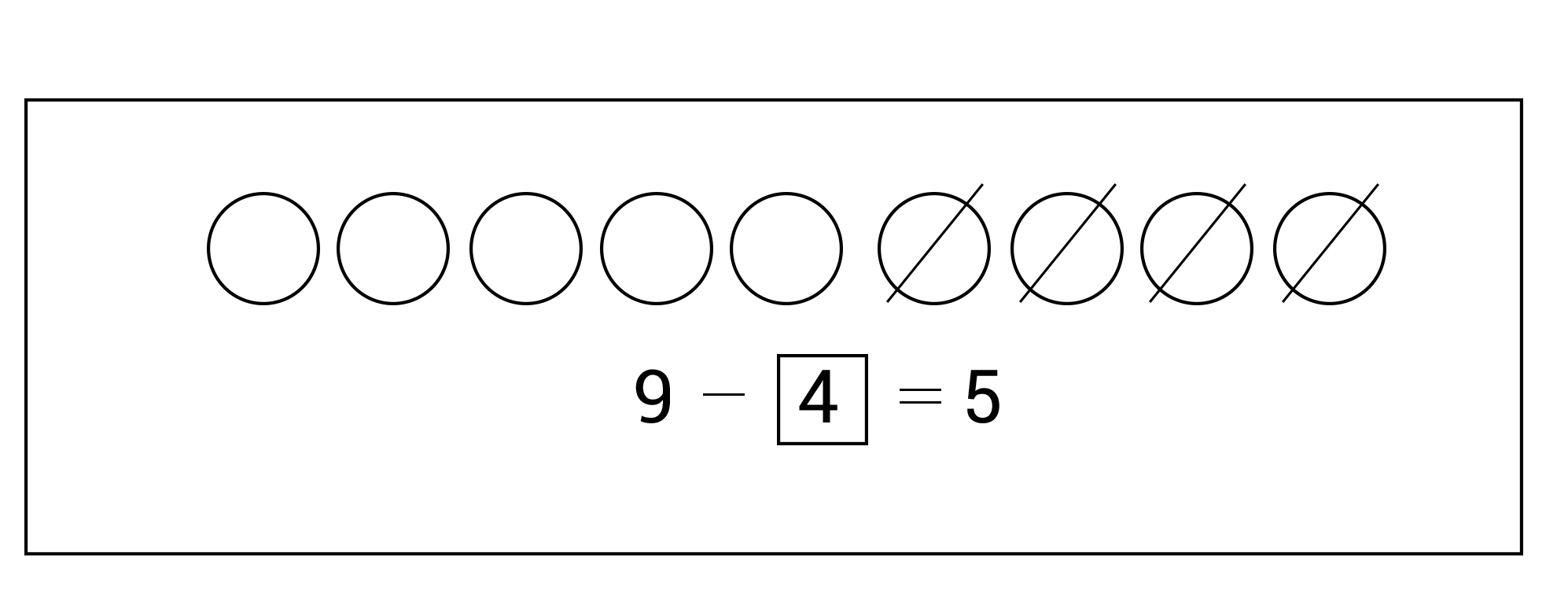
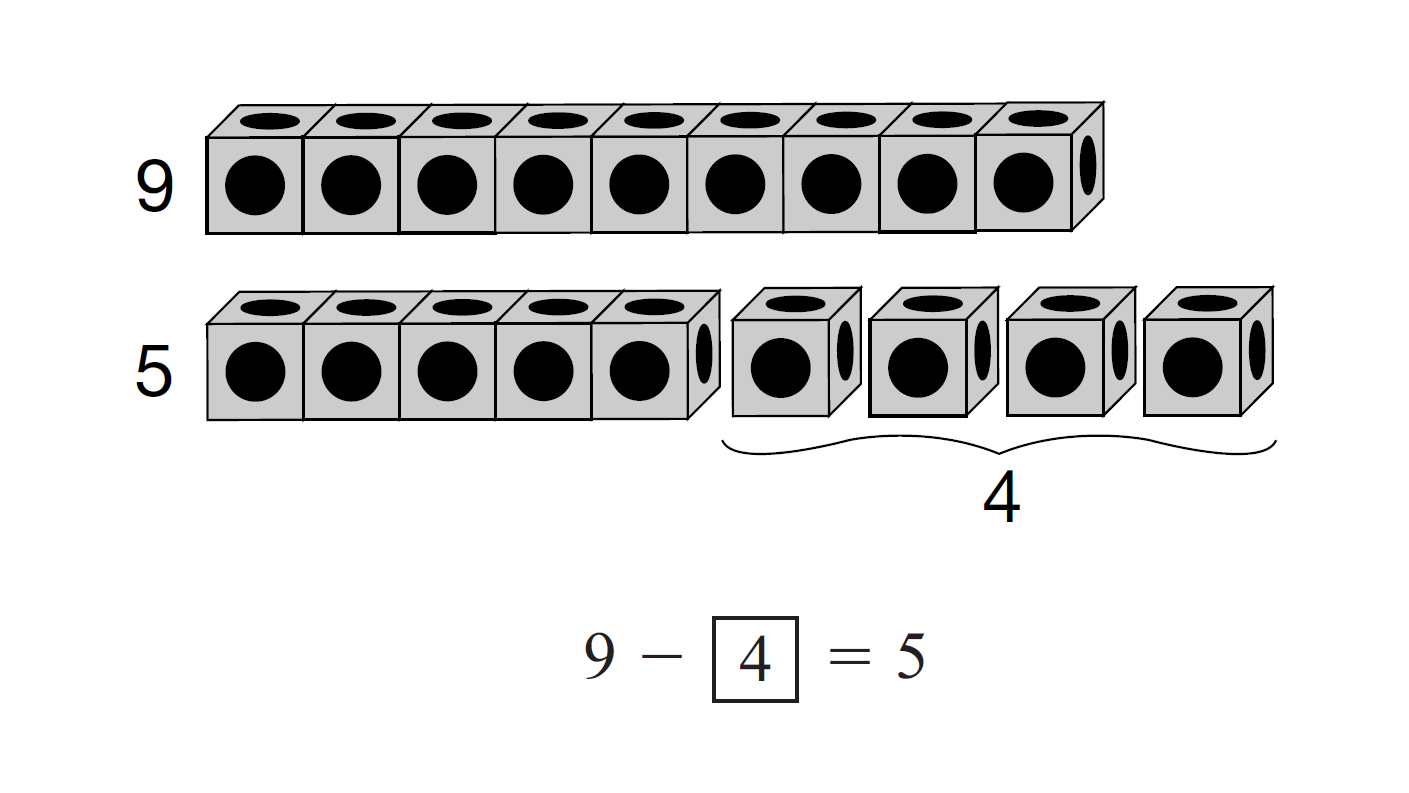
9 − = 5

Ask:

X
  • What do you notice about this number sentence? (Possible response: There is a box and a missing number.)
  • Talk with your partner and decide what number should be in the empty box to make this a true number sentence. Show how you know. (4; Possible response: We drew a picture of 9 circles. We knew we had to take some until we had 5 left. We counted back and took one off until we had 5: 8, 7, 6, 5, four times. 9 circles minus 4 circles is 5 circles. See Figure 3.)
  • How can we check this answer to make sure it is correct? (Possible response: We could use a different tool, or a different method from the chart. We should get the same answer.)
  • Is there a way to check with cubes? (Possible response: I built a train of 9 cubes and a train of 5 cubes. I put them next to each other. I needed to add 4 cubes to the 5-cube train to make 9, so I know the missing number is 4. See Figure 4.)
  • Did anyone think about addition? How could thinking addition help to solve the problem? (Possible response: I thought, "What number put together with 5 would make 9? 5 + 4 = 9.")

Display the following number sentence:
4 = 9 −

Ask:

X
  • What do you notice about this number sentence? (Possible response: There is a missing number. The equal sign comes near the beginning of the number sentence. It is similar to the other number sentence.)
  • What do you know about true number sentences? (Each side of the equal sign has to have the same value, so each side of this one has to be 4.)
  • What number is missing? How did you decide? (5; Possible response: First I flipped the question around to be 9 − = 4 because it was easier for me to think about. If 9 − 4 = 5, then 9 − 5 = 4. They are in the same fact family. 5 goes in the box. 4 = 9 − 5.)
  • How can fact families help you find missing numbers? (Possible response: If you know one of the facts in the fact family, it can help you figure out the other three. I think about how they are related.)
  • Does 4 + 5 = 5 + 4? (Yes, because they are turn-around facts.)
  • Does 9 − 5 = 9 − 4? Why or why not? (No, because the one on the left of the equal sign is 4 and the one on the right of the equal sign is 5.)
  • Does subtraction have a turn-around rule? (no)
Display the following number sentences one at a time:
  1. 8 + 3 = 9 +
  2. 8 + = 3 + 8
  3. 4 + 4 + = 11
  4. 11 = − 3

Ask students to work with their partners to find the missing numbers that will make each number sentence true. Remind students that the empty boxes represent one missing number. Encourage them to use tools to solve the problems. Have student volunteers share their strategies for making the number sentences true. Add any new methods to the class chart. The Sample Dialog discusses students' reasoning for finding missing numbers.

X
This sample dialog discusses students' reasoning for finding missing numbers.

Teacher: Let's look at 2 + 3 = + 2. What number should be in the empty box to make the first number sentence a true number sentence? Tell me your thinking.

Shannon: Five goes in the box. I added 2 and 3 and that's 5.
Nicholas: I think that 3 goes in the box. It has to be the same on both sides, so 2 + 3 is the same as 3 + 2.

Teacher: Let's look at these choices and decide which one makes a true number sentence. [The teacher writes the number sentences on the board.]

2 + 3 = 5 + 2
2 + 3 = 3 + 2
Remember that the numbers on both sides of the equal sign must equal the same thing. Think of tools and words to explain your thinking.

Shannon: We think Nicholas is right. We looked at the first one. Keenya said we had to make a train for each side. [Shannon shows a train of five cubes and one of seven cubes.] See they aren't the same. So, five can't go in the box.

Teacher: Show the class your trains again. Let's look at both sides of the number sentence. On this side, we have 2 + 3. How many cubes are in that train?

Shannon: 5.

Teacher: And on this side, we have 5 + 2. How many cubes are in that train?

Shannon: 7. [Teacher writes 5 and 7 below each side of the number sentence.]

Teacher: So, this is a false number sentence.

2 + 3 = 5 + 2
  \   /          \   /
   5              7         False
2 + 3 = 3 + 2
What about Nicholas' number sentence. Is it true?

Ming: It's right. I know that you can turn around the 2 and 3.
2 + 3 is the same as 3 + 2.

Teacher: We call those turn-around facts. How could you show them that 2 + 3 is the same as 3 + 2? What tools could you use?

Ming: I'd use a number line.

Teacher: How would you use it? Show us on the class number line.

Ming: I'd start at 2 and hop like this. Then I'd start at 3 and go like this. [Ming starts at 2 and then makes three little hops to 5. Then, he starts at 3 and makes 2 little hops to 5.] See, you end up at 5 both times.

Teacher: So, 2 + 3 = 5 and 3 + 2 = 5, too. [She writes the following on the board.]

2 + 3 = 5 + 2
  \   /          \   /
   5              7         False
2 + 3 = 3 + 2
  \   /          \   /
   5              5
    True

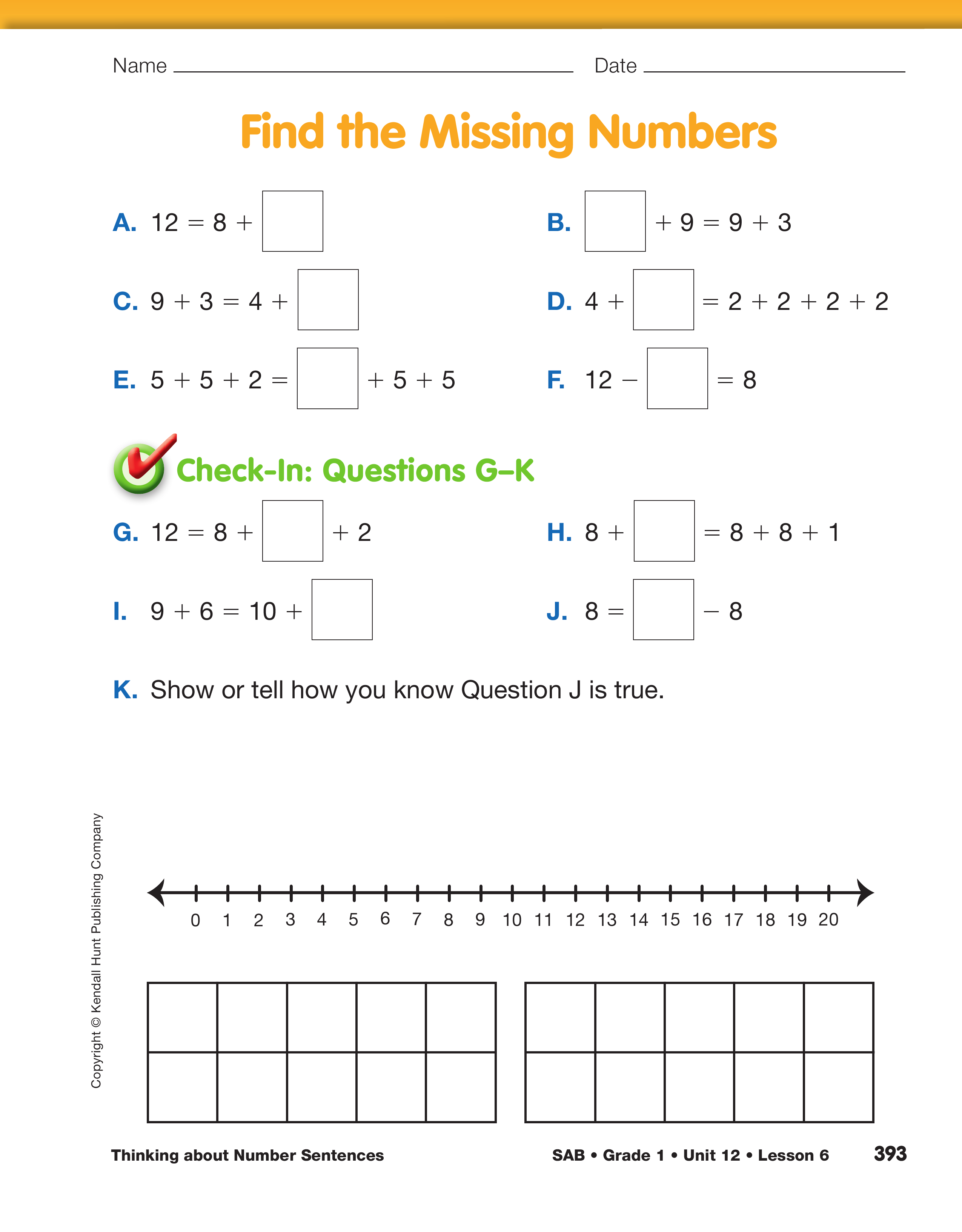
Ask students to complete the Find the Missing Numbers page in the Student Activity Book. As students work, talk with them about their thinking. Encourage them to use tools when appropriate.

As you monitor students' work, ask:

X
  • How did you use a tool to find one of the missing numbers?
  • How did you find this missing number?
  • How do you know this number sentence is true?
  • I see you like to use [cubes] a lot. Can you try using a [number line] for this one?
  • What do the numbers on this side of the equal sign equal? The other side?
  • Which problem is the most challenging so far? Why?

Note if students are just adding the numbers on the left side of the equal sign and putting the sum in a box or if they understand that the expressions on each side of the equal sign must, in fact, be equal.

When students have completed the page, ask volunteers to share their strategies for finding missing numbers in several questions, and discuss any questions they found particularly challenging.

X

Use Check-In: Questions G–K on the Find the Missing Numbers page in the Student Activity Book to assess students' progress toward recognizing that the equal sign represents the relationship between two equal quantities [E4]; finding the unknown whole number in an addition or subtraction equation relating three whole numbers [E7]; finding a strategy and using good tools [MPE2]; and showing or telling solution strategies [MPE5].

Student Guide:
Student Activity Book: 393
Answers
X
SAB_Mini
+
Master:
Using a drawing to help find the missing addend
X
+
Comparing cube trains to help find the missing addend
X
+