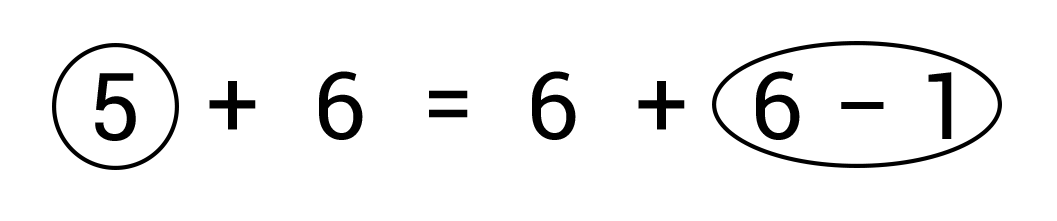The Equal Sign. The equal sign signifies a relation between
two numbers. Understanding that the equal sign means that
expressions on the two sides of the equal sign represent the
same numerical value is an important mathematical concept.
Experiences that allow students to explore these ideas now
will help them avoid common misconceptions later. For
example, students who see only number sentences of the
form 3 + 2 = 5 often come to the erroneous conclusion that
the equal sign means, "The answer comes next" or "Do the
operation."
Using the equal sign flexibly will allow students to represent
their thinking more easily. For example, students can say that
they know that 9 + 4 is 13 because 9 + 4 = 10 + 3.
What to Avoid. Researchers caution against using the equal
sign in ways in which it does not represent a relation
between numbers. For example, avoid expressions such as
"Jerome = 3 feet" or "Sara = 6." Similarly, it is not appropriate
to draw a picture of three objects and then write
"★★★ = 3". Save the equal sign for representing relations
between numbers.
It is also important to avoid writing number sentences that
chain calculations together. For example, a partitioning strategy
can be used for adding 10 + 17 = 27. However, avoid
writing 10 + 10 = 20 + 7 = 27, because 10 + 10 does not
equal 20 + 7 (Carpenter, et al., 2003; NCTM, 2000).
Introduce True and False. To begin the lesson, display
the following sentences:
- My name is [insert your name].
- My name is [insert a false name].
- [Insert your name] is my name.
- [Insert a false name] is my name.
Discuss the sentences.
- What can you say about these sentences?
- Which are true and which are false?
-
How can Sentence A and Sentence C both be true?
(Possible response: They say the same thing—the
order is just different.)
Display the following number sentences:
A. 4 + 2 = 6
C. 5 + 2 = 6
B. 6 = 4 + 2
D. 6 = 5 + 2
Discuss these number sentences using similar
prompts:
- What can you say about these sentences?
-
Which are true and which are false? How do you
know? (Possible response: Sentences A and B are
true and Sentences C and D are false. I know
4 + 2 = 6 so 5 + 2 would be one more, 7, not
6.)
-
How can Sentence A and Sentence B both be true?
(Possible response: They say the same thing—the
order is just different.)
Use Tools and Strategies. Display the following
number sentences one at a time, giving students time
to talk with a classmate about each one:
- 6 = 6
- 4 + 2 = 2 + 4
- 4 + 2 = 3 + 3
- 4 + 2 = 6 + 0
- 6 = 10 − 4
For each number sentence, ask students to discuss
the following with their partners:
- Is the sentence true or false?
-
How can you show that the sentence is true [or
false]? What tools can you use?
Encourage students to consider the tools that they
have used in class to solve problems and to find a
way to use at least one of the tools to show their
thinking.
For example, ask questions similar to the
following and have students use models to justify
their reasoning:
-
How can you show that 4 + 2 = 2 + 4? (Possible
response: It's a turn-around fact. Also, if I make
one train with 4 red cubes and 2 yellow cubes
and another train with 2 red cubes and 4 yellow
cubes, they are the same length.)
Complete each conversation by representing the
addition on both sides of the equal sign as follows:
4 + 2 = 2 + 4
\ / \ /
6 6
True
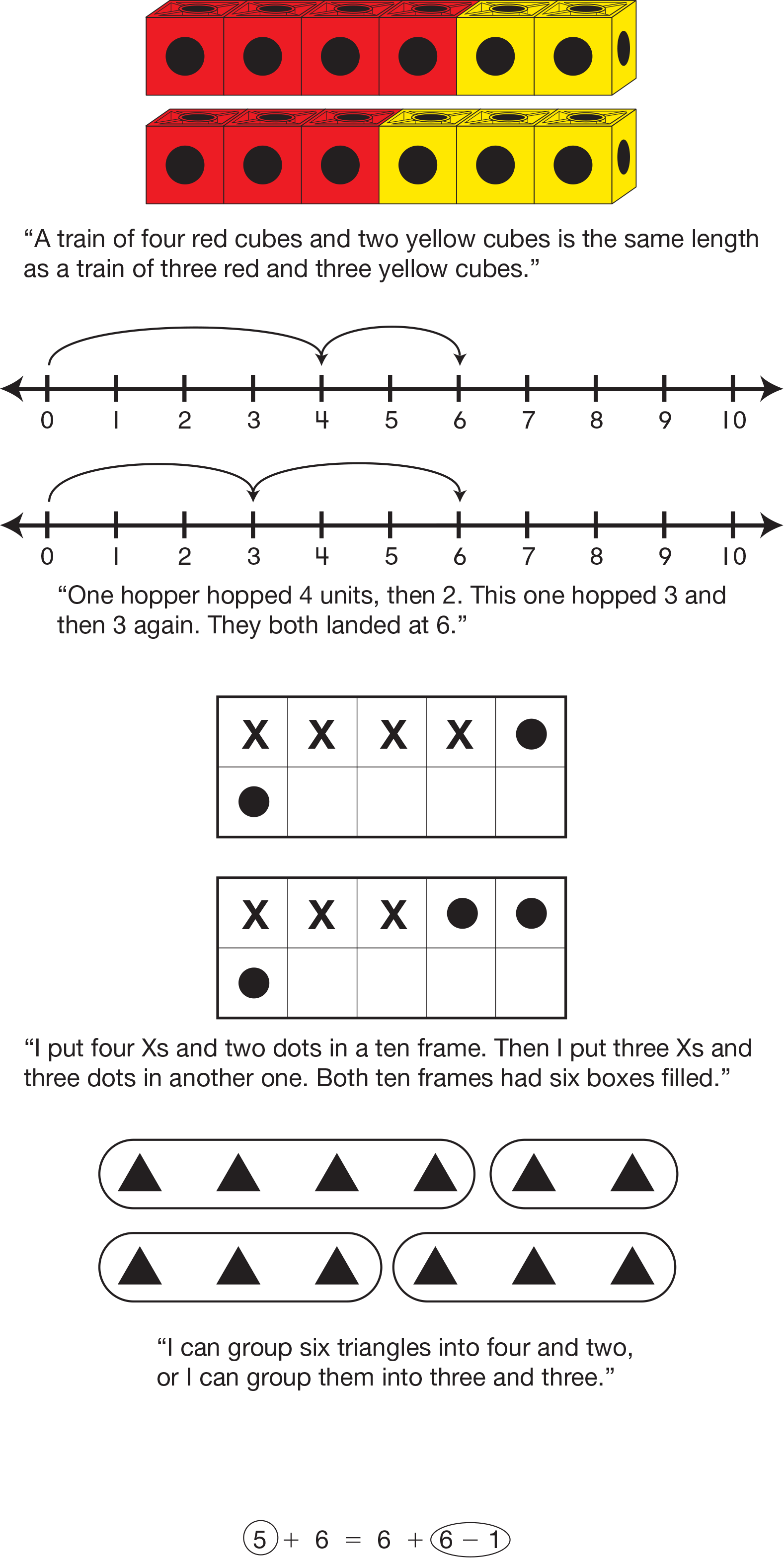
Figure 1 shows several methods for showing that
4 + 2 = 3 + 3 (Sentence C) is true. Ask students to
share their methods by showing how they used the
tools either verbally or in a picture. Record students'
methods on chart paper. Label the methods with
either the students' names or the names of the tools
so that you have an efficient way of referring to the
methods later.
Note that during the discussion, students can use
strategies or models to interpret the number sentences,
but they may not always do so. They may
just look at number sentences without solving them.
For example, some students may reason that
4 + 6 = 4 + 5 + 1 without actually solving the
problem because they see that the 6 on the left side
of the equation is equal to the 5 + 1 on the right side
of the equation, resulting in a balanced equation.
Students may also consider the properties of addition,
such as the commutative or turn-around property,
and the associative property as they compose
and decompose numbers and determine whether a
number sentence is true. See Content Note. Help students
look for patterns in the composition and
decomposition of the numbers to decide if it is true.
Revise False Number Sentences. Display the following
number sentences:
- 5 + 6 = 10 + 1
- 11 = 8 + 2
- 5 + 6 = 5 + 5 + 1
- 5 + 6 = 12 − 1
- 5 + 5 = 6 + 6 − 1
Assign the number sentences to different pairs of
students. Ask them to decide if the statement is true
or false and to be prepared to explain how they
know.
After student pairs have worked on their sentences,
discuss which ones are true and which are false.
Sentence B and Sentence E are false.
Discuss how to
rewrite the sentences to make them true by asking:
-
Is 11 = 8 + 2 true or false? How do you know?
(False; If I start at 8 on a number line and hop 2
more, I land on 10, not 11.)
-
How can you change the number sentence to
make it true? (Possible response: 11 = 8 + 3)
-
How can you use a method on the chart to check
that number sentence to make sure it is true?
(Possible response: I think about 8 dots in a ten
frame plus 3 more. It makes a ten and one, 11.)
-
How did you decide if 5 + 5 = 6 + 6 − 1 was true
or false? (Possible response: I know the doubles
5 + 5 = 10 and 6 + 6 = 12. Both sides of the
equation have to be true, but one side is 10 and
the other side is 12 − 1 = 11. It is false.)
-
How can you make it a true number sentence?
(Possible response: 5 + 6 = 6 + 6 − 1)
-
How can we be sure it is true now? (Possible
response: Both sides of the equal sign have to be
the same, so I see a 6 on each side. There is a 5
on the left and that is the same as the 6 − 1 on
the right side. See Figure 2.)

Commutative Property of Addition. The commutative property
of addition says that the order in which the addends are
added does not affect the sum of the problem. Both
3 + 2 and 2 + 3 equal 5. When two numbers are added, the
sum is the same regardless of the order of the addends.
In order to help students appreciate the commutative property
of addition, ask them to consider whether or not subtraction
is commutative. It is not. When subtracting, the
order in which numbers are subtracted will change the difference.
Associative Property of Addition. The associative property
of addition says that when adding three or more numbers,
the way addends are grouped does not matter. For example,
(2 + 3) + 4 = 2 + (3 + 4). When three or more numbers
are added, the sum is the same regardless of the grouping of
the addends.
Helping students appreciate the associative property of addition
may be facilitated by asking them to consider whether or
not subtraction is associative. Addition is associative;
(2 + 3) + 4 and 2 + (3 + 4) both equal the sum of 9.
Subtraction is not associative; (4 − 3) − 2 = −1,
but 4 − (3 − 2) = 3.
Important note: In first grade, students do not need to know
the terms "Commutative" and "Associative" but do
need to understand how to use the properties.
Assign the True or False page in the Student Activity
Book to student pairs. Students will determine
whether number sentences are true or false. One of
the number sentences is false and will need to be
rewritten so that it is true.
Use Check-In: Questions F–G on the True or False page in the
Student Activity Book to assess students' abilities to recognize
that the equal sign represents the relationship between two
equal quantities [E4]; choose a good tool or strategy [MPE2];
and explain their work [MPE5].
-
Were any of the sentences false? (Sentence C)
-
How did you know it was false? (Possible
response: I thought about 10 dots in a frame and
then 3 more in another one. I put 10 in my head,
then counted 11, 12, 13. The other side of the
equal sign 13 + 10 was much more than 13, ten
more.)
-
How can you rewrite it to make it true? How do
you know it is true? (Possible response: 10 + 3 =
3 + 10 is true because it is a turn-around.)
-
Show how you know sentence [A, B, D, or E] is
true.
-
Find another way to show that sentence [A, B, D,
or E] is true. Should we add that method to the
chart?
-
Use [student name]'s method of showing this sentence
is true.
Assign the Missing Numbers Homework Master.
This page reviews missing addend problems similar
to those that they have completed before but with
sums to 20.