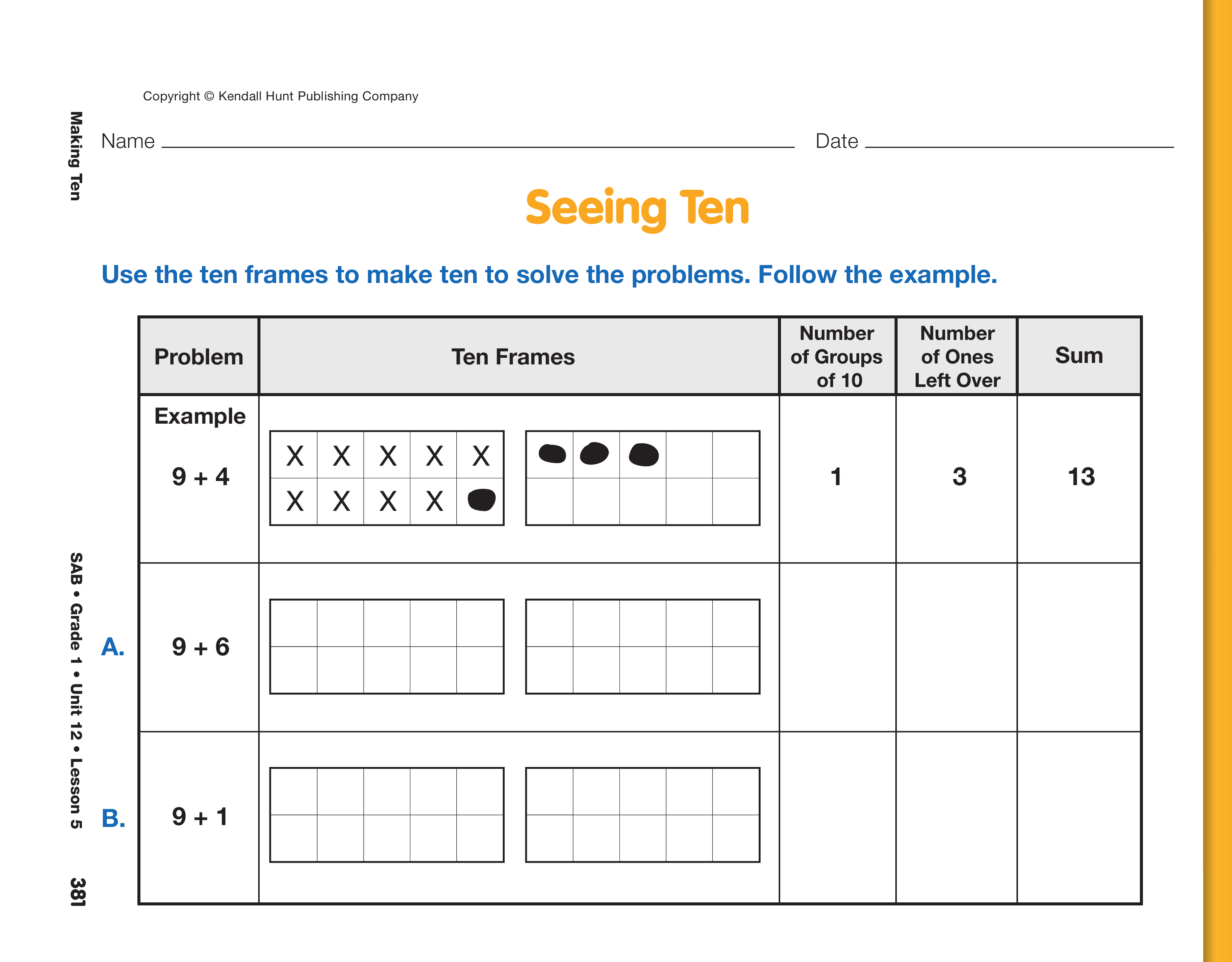
Finding the Sum of 9 and 4.
Write the following
number sentences on the board and ask students to
solve them:
7 + 3 + 4 =
9 + 1 + 2 =
5 + 5 + 6 =
2 + 8 + 5 =
After they have solved the problems, ask students if they "see" the tens. Ask them how using the tens can make it easier to solve the problems.
Ask students to work in pairs to solve the following
problem in at least two ways:
Grace and Jerome collect stickers in a book.
Grace put in 9 stickers and Jerome added 4 stickers.
How many stickers did they put in their book
altogether? Show or tell how you solve the problem.
Remind students that they can use any of the tools
they have been using in class, including their connecting
cubes, number lines, ten frames, or 100
Charts. Give student pairs copies of the Eight Ten
Frames Master that they can write on. They can also
make a diagram or drawing to explain their thinking.
Ask students to share their strategies on chart paper
so that there is a class record of the strategies. Have
displays of ten frames and a 100 Chart available. As
students report their strategies, encourage other students
to ask questions if they do not understand the
speaker's explanation. Emphasize that all these
strategies resulted in correct answers. Then ask students
to discuss which one(s) were the most efficient
and why. Ask students to vote for the strategy that
they find easiest to use. See the Sample Dialog.

Students explain their strategies for solving 9 + 4 then discuss which are the most efficient and why.
Teacher: Maya, show us how you and Ming solved the problem. Write your names beside your work.
Maya: [Draws a group of nine squares and four squares on the board.] We drew 9 stickers and then we drew 4 stickers and then we counted them. There were 13.
Teacher: Does everyone understand, Maya and Ming's method? How do you think they counted?
Jackie: They just counted: 1, 2, 3, to 13. Like that.
Teacher: Is that how you counted Maya? Ming? [Ming and Maya nod.] Is there a quicker way to count? Jacob, can you come show us?
Jacob: I just used my fingers. I started at 9 and counted 10, 11, 12, 13. [Shows counting 10 to 13 on four fingers.] They could have just started at nine and counted four more.
Teacher: Let's do what Jacob suggested. Let's start at 9. [The teacher writes 9 beside the group of 9 stickers, then points to the group of 4 stickers.]
Class: 10, 11, 12, 13. [Teacher writes 10, 11, 12, 13 by each of the four stickers.]
Teacher: I am going to write Jacob's name by these numbers to remind us of the way Jacob counted. Did anyone use a different tool or strategy?
Shannon: I used cubes. I made a stack of 9 cubes and a stack of 4 cubes, then I put them together and I counted them all.
Teacher: That is very similar to the way that Ming and Maya did it, except that Shannon used cubes. Is there a quick way to count Shannon's cubes?
John: Here is what I thought. [John comes to the front of the room and separates the cubes into stacks of nine and four again. Then he takes one cube from the stack of four and adds it to the stack of nine.] Now I have a stack of ten and three. It is like when we did the teens:
10 + 3 = 13.
Teacher: Does everyone understand John's method? [A few students say, "No."] Ask John a question so that he knows what you don't understand.
Jerome: The problem is 9 and 4, not 10 and 3, so I don't understand why you made a stack of ten.
John: Ten is easy to add. So I just moved one cube from the four stack to the nine stack. Now it is easy, 10 + 3 = 13.
Teacher: Those are all interesting strategies. Which strategy do you think is the easiest to use? Why do you think so?

Class discussions should affirm students' reasoning and use
of strategies so that all students feel confident in sharing
their thinking and making conjectures about the use of
strategies. Different students will progress toward more efficient
strategies at different rates. Acknowledge individual students'
progress, whether it is a move from counting all to
counting on or a move toward reasoning from known facts.
Class votes are a means of probing students' comfort with
different types of strategies. A vote allows the less verbal students
to also have a voice in evaluating the different strategies.
A short discussion of students' preferred strategies can
serve the same purpose. Alternatively, students can write
their choice on an individual white board or piece of scrap
paper and use it to vote silently.
Don't assume that the students will recognize the
most efficient strategies at first. With additional
practice and experience with the more sophisticated
strategies, students should begin to choose them.
Finding the Sum of 9 and .
Direct students'
attention to the display of the Linda's Strategy
Master. On this page, a student describes her method
of solving 9 + 4. She fills in ten frames to "see a
ten." Discuss Linda's method.
- What tool did Linda use to solve the problem? How did she use it?
(Possible response: Linda
used a ten frame. She put nine Xs and then one of
the dots in the first ten frame. Then she put the
last three dots in the next ten frame.)
- What did Linda mean when she said, "I saw a 10 and 3 ones"? Where did she see the ten and three ones?
(Possible response: The 10 is in the first
ten frame. The 3 ones are in the next ten frame.)
- What is the partner number for nine to make a ten? Nine plus what number makes ten?
(One is the
partner number for nine. 9 + 1 = 10)
- Where did the one come from to add with nine to make ten? How did Linda make a ten with the numbers in the problem?
(Possible response: She
used one dot from the four to put in the first ten
frame. That made ten.)
- How many dots were left over in the second ten frame?
(three dots)
- Linda changed the problem from 9 + 4 to 10 + 3. Can you tell how she did that?
(She took one from
four to make a ten with the nine. Then she added
the ten and the three that were left. 10 + 3 = 13)
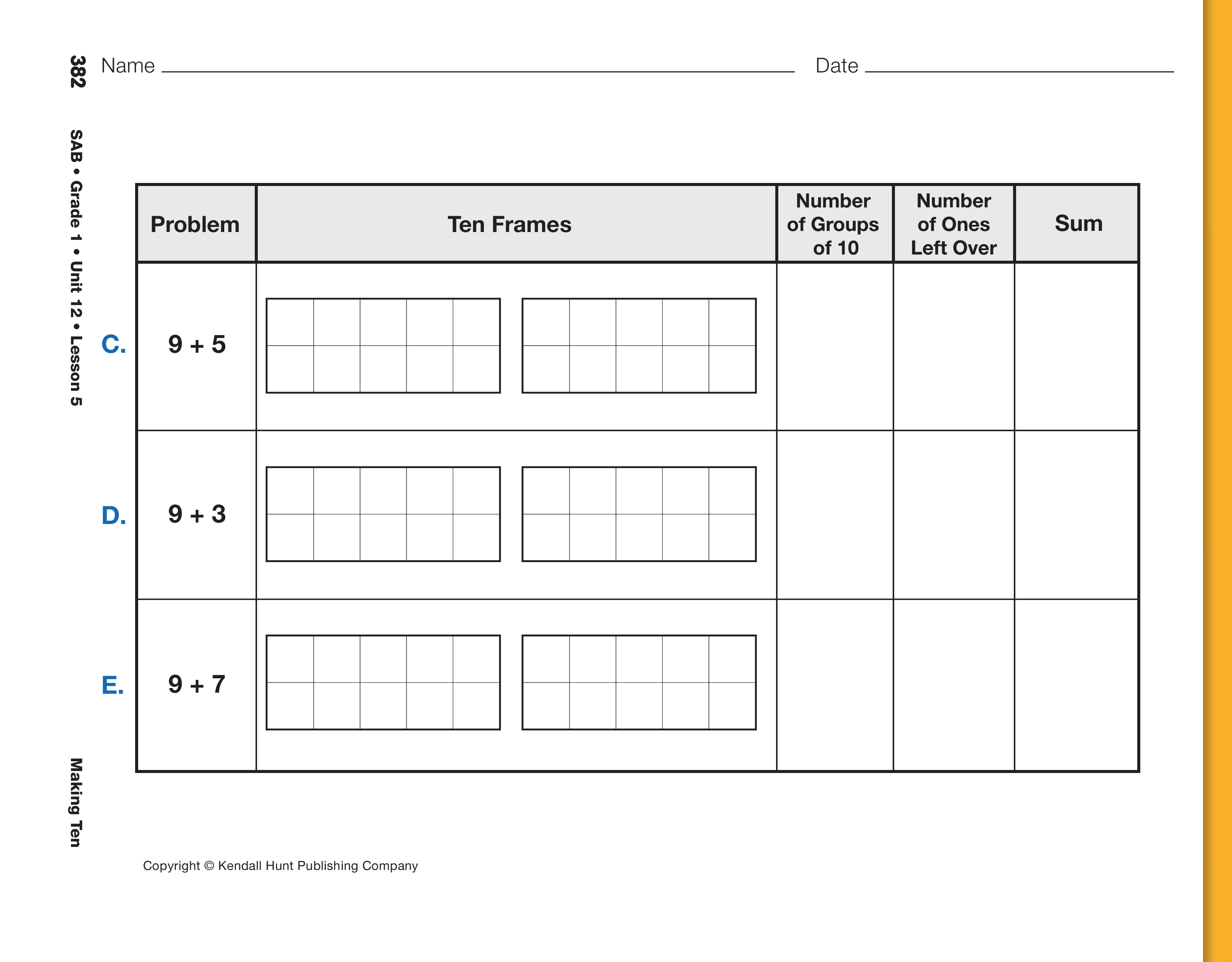
Ask students to complete the Seeing Ten pages in the
Student Activity Book following the example. Be
sure students fill in the first ten frame completely
before beginning the second. As students complete
the pages, talk with them about their reasoning using
prompts similar to those you asked about Linda's
strategy. A summary of the prompts is in the Meeting
Individual Needs Box.
When students complete the pages, ask them to work
with their partners to solve the problem below in two
ways.
9 + 8 =
Discuss students' use of tools and strategies. Possible strategies include:
- Direct modeling and counting all using connecting cubes;
- Using fingers or the number line to count on from 9 to 17;
- Using the ten frames to "make a ten" as on the student pages;
- Using doubles minus one, e.g., 9 + 9 = 18, so 9 + 8 is one less or 17;
- Visualizing making a ten, changing 9 + 8 to 10 + 7.
Some students may already be able to "see tens" and use the
making-ten strategy to solve problems with sums less than
20. Ask these students to use the same strategy to solve the
following problems: 19 + 4, 29 + 4, 18 + 4, 28 + 4,
17 + 4,
27 + 4.
Use the prompts to talk with students as they make tens to solve the problems.
- Do you see a ten in the problem? Show me.
- What is the partner number with 9 [8, 7, 6] that makes ten?
- How can you make a ten with the 9 [8, 7, 6]?
- If you take a one from ______ [the second addend] to make ten, what will be left over to add to the ten?
- Does making a ten help you solve the problem? How?
Ask students to vote again on the strategies that they
find the easiest or most efficient. Discuss the use of
the making-ten strategy, either with the ten frames or
if students can verbalize their thinking. Write the following
number sentences on the board:
9 + 8 = 17
9 + 1 + 7 = 17
- How are the sentences alike?
(Possible responses: They both add up to 17. Both have a 9 in them.)
- How are they different?
(Possible responses: One has two numbers to add. The other has three numbers.)
- Do you see a ten in the second sentence? Where is it?
(9 + 1 = 10)
- Do you see a ten in the first sentence? Can you make a ten in the first sentence? How?
(Take one from the 8 and add it to the 9.)
- Does that make it easier to solve the problem? How?
(Then you can think 10 + 7 and that is easy to add, it's 17.)
As the class is discussing the sentences, one way to
show students' reasoning is to circle the 9 and 1 to
highlight the 10 and note that the 8 is separated into
1 and 7 as shown below.
9 + 8 = 17
/ \
9 + 1 + 7 = 17
10 + 7 = 17
It is unlikely that students will be able to represent
their thinking in this way. However, it is useful for
you to begin modeling the problem with symbols.
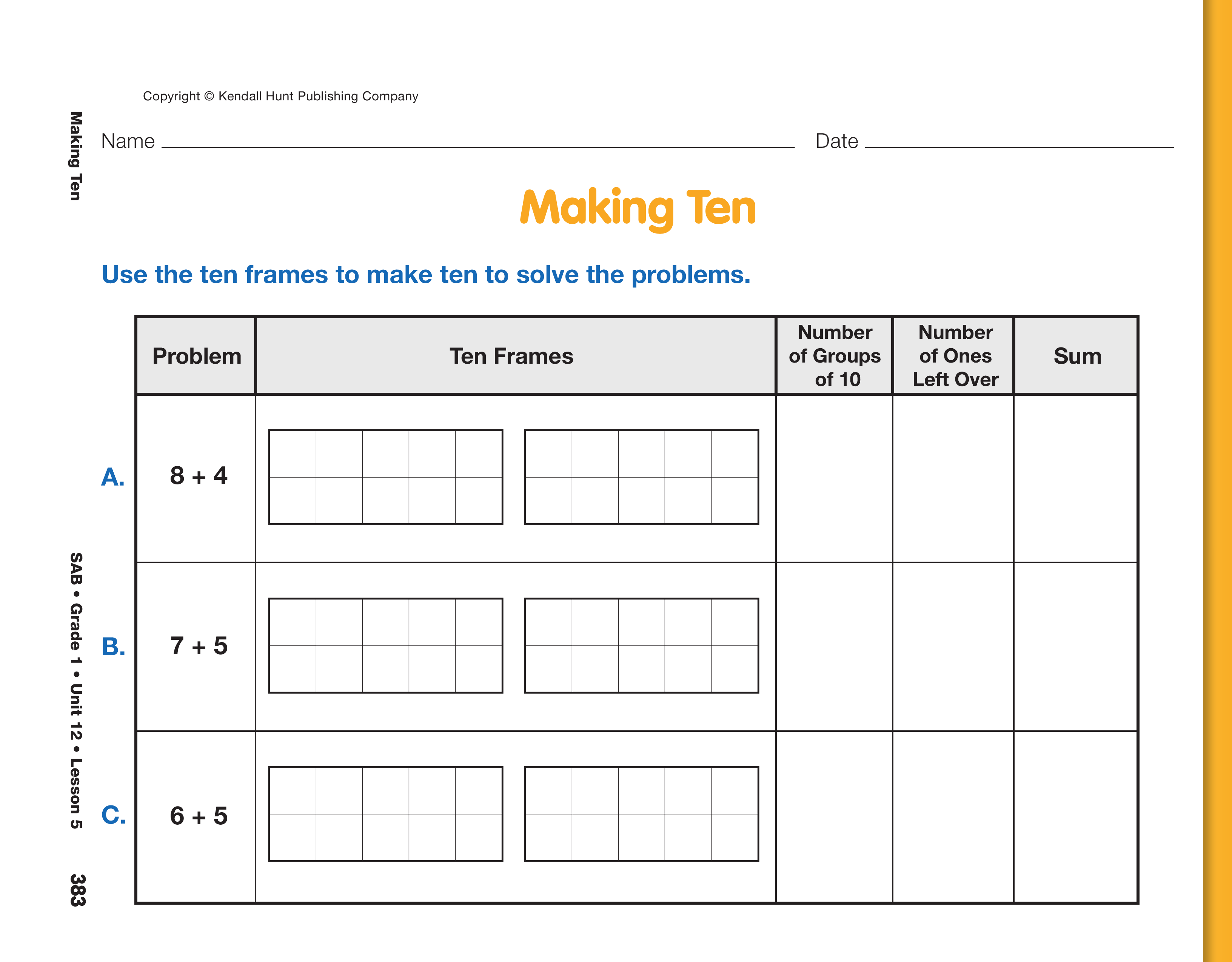
Breaking Apart to Make Ten.
Ask students to complete
the Making Ten pages in the Student Activity
Book. In these pages, students use ten frames to "see
tens" as they solve addition problems with addends
of 8, 7, and 6 (e.g., 8 + 5, 7 + 5, 6 + 5). As they
work, talk with students using prompts similar to
those in the previous discussion. In particular, talk
with students about partner numbers that make ten.
Guide students in completing 18 + 4 on the Making
Ten with Larger Numbers pages in the Student
Activity Book as you elicit input from the class.
Discuss similarities and differences between this
problem and those on the Making Ten pages.
Emphasize discussion about partner numbers that
make tens.
Have students complete the remaining problems on
the page independently or in pairs as appropriate for
your class. Refer to discussion prompts previously
used as students work, then discuss solutions.