Think about Addition and Subtraction
MATH FACTS STRATEGIES in FIRST GRADE

In this unit, students focus on further developing their understanding of addition and … read more
In this unit, students focus on further developing their understanding of addition and subtraction. Specifically, students are asked to grapple with moving from less efficient (direct modeling and counting strategies) to more efficient reasoning-from-known-facts strategies. Students have been gaining fluency with the partners or partitions of ten and the facts that are efficiently solved with counting strategies. Students will use this knowledge to develop strategies for problems with larger sums (e.g., 6 + 7 or 8 + 9).
Development of Math Facts Strategies
In accordance with the National Council of Teachers of Mathematics Principles and Standards for … read more
Development of Math Facts Strategies
In accordance with the National Council of Teachers of Mathematics Principles and Standards for School Mathematics, the Curriculum Focal Points (NCTM 2000, NCTM 2006) and the Common Core Standards for Mathematics, Math Trailblazers students are expected to achieve fluency with the addition and subtraction facts by the end of second grade. Students work toward this goal by solving addition and subtraction problems in ways that make sense to them. Students also approach the math facts by systematically developing efficient strategies for the facts that will help them learn other facts. For example, the facts with sums of ten (e.g., 8 + 2 and 6 + 4) can help develop make-ten strategies for solving facts with larger sums (e.g., 8 + 7 and 6 + 8).
There is a body of research that supports students working toward math facts fluency in this manner. Generally, students move through three developmental stages when acquiring operational understanding and fluency with the math facts:
- Direct modeling in which students re-create the action in the problem using manipulatives;
- Counting strategies such as counting on and counting back; and
- Reasoning from known facts in which students work from facts they already know. If, for example, a student knows that 6 + 4 = 10, then he or she has a quick way to access 7 + 4 (Carpenter, 1999, National Research Council, 2001).
STRATEGIES for REASONING from KNOWN FACTS

In Unit 6, students developed an Addition Strategies Menu for Small Numbers to encourage … read more
In Unit 6, students developed an Addition Strategies Menu for Small Numbers to encourage students to think about efficiency and appropriateness of a strategy. In this unit students will revise this menu to develop an Addition Strategies Menu for Larger Numbers. This activity happens in Lesson 7. See Figure 1. Notice the strategies are the same, but students need to apply them to larger numbers and, therefore, refine the examples.
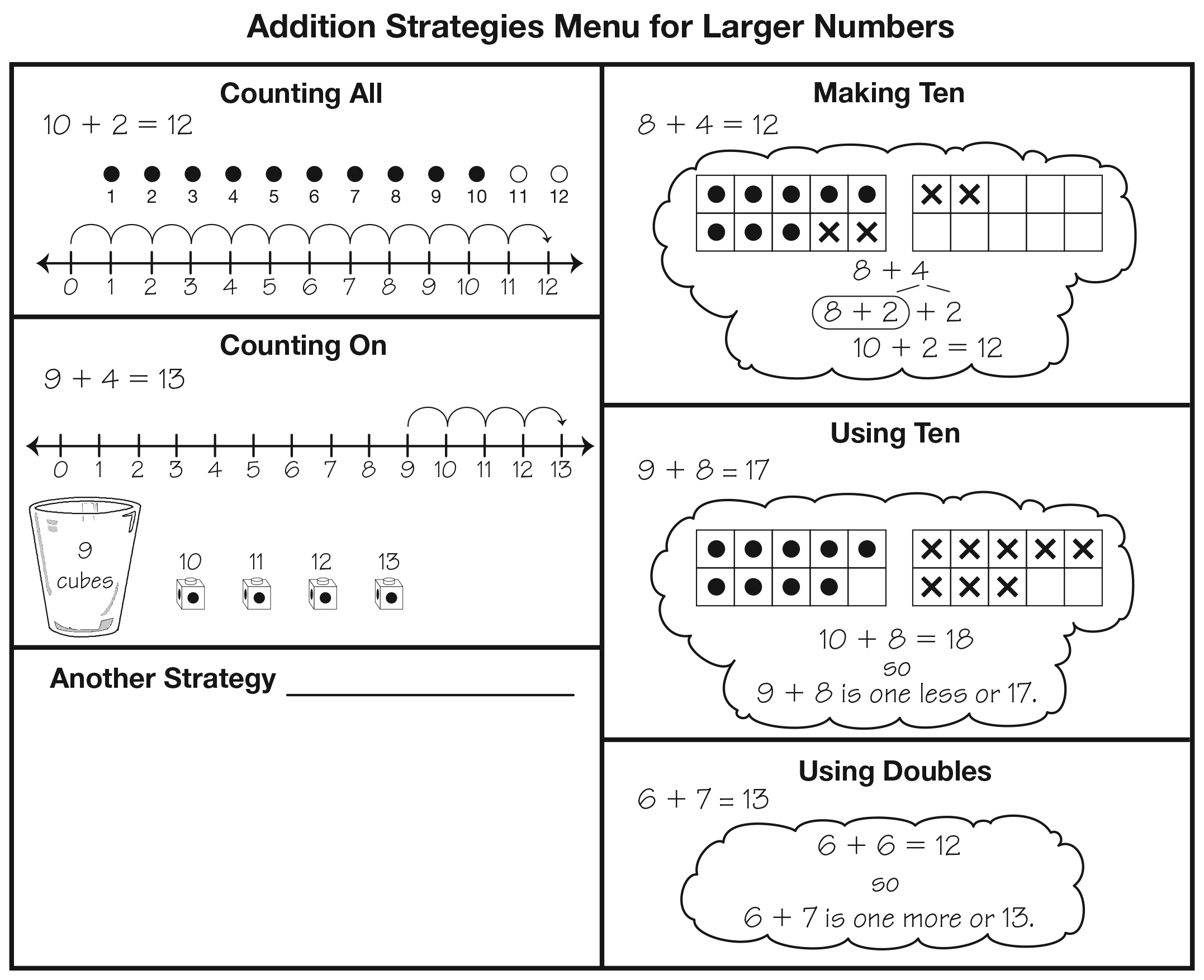
Figure 1: Addition Strategies Menu for Larger Numbers developed in Lesson 7
Using Doubles
Doubling is a natural and appealing strategy that some young children develop before … read more
Using Doubles
Doubling is a natural and appealing strategy that some young children develop before entering school. It is not unusual, for example, for young children to simply announce that "I know that 3 and 3 is 6" or "5 and 5 is 10." Students naturally extend their knowledge of doubling to multiples of 10 and other larger numbers.
Doubling is useful in learning other basic facts. Students readily understand that the sum of 5 and 6 is 1 more than 5 and 5 and, therefore, use a known double to find the answer to a related fact called a near double. Many students make other uses of doubles. Some students find the answer for 5 + 7 by counting 2 more from the double 5 + 5, whereas others use 6 + 6 to find the answer. Doubles are also useful for related subtraction facts. Many students, for example, respond quickly without counting for subtraction facts that involve a double, such as 8 – 4 and 12 – 6. Using doubles also seems to be useful with large numbers such as 40 + 40 or 25 + 25.
An idea closely related to doubling a number is finding half of a number, or halving. Knowing that 10 and 10 is 20 provides a natural bridge to determining that 10 is half of 20. While students' initial classroom experiences with doubling and halving often involve using manipulative materials, they are also able to work with these ideas mentally. Finally, working with doubling and halving numbers builds conceptual readiness for multiplication.
Making Ten
This a second and very important strategy developed in this unit. Because this strategy is based on … read more
Making Ten
This a second and very important strategy developed in this unit. Because this strategy is based on composing and decomposing ten and other numbers, students will be able to build upon it to help them solve multidigit addition and subtraction problems. Making a ten takes advantage of students' prior experience with partitions of ten when using the ten frame. Students are already familiar with facts that "make ten" such as 8 + 2 and 6 + 4. Students reason from these known facts to find sums for addition facts such as 8 + 5. For the problem 8 + 5, students can first add 8 and 2 to make 10 and then add 3 to 10. See Figure 2.
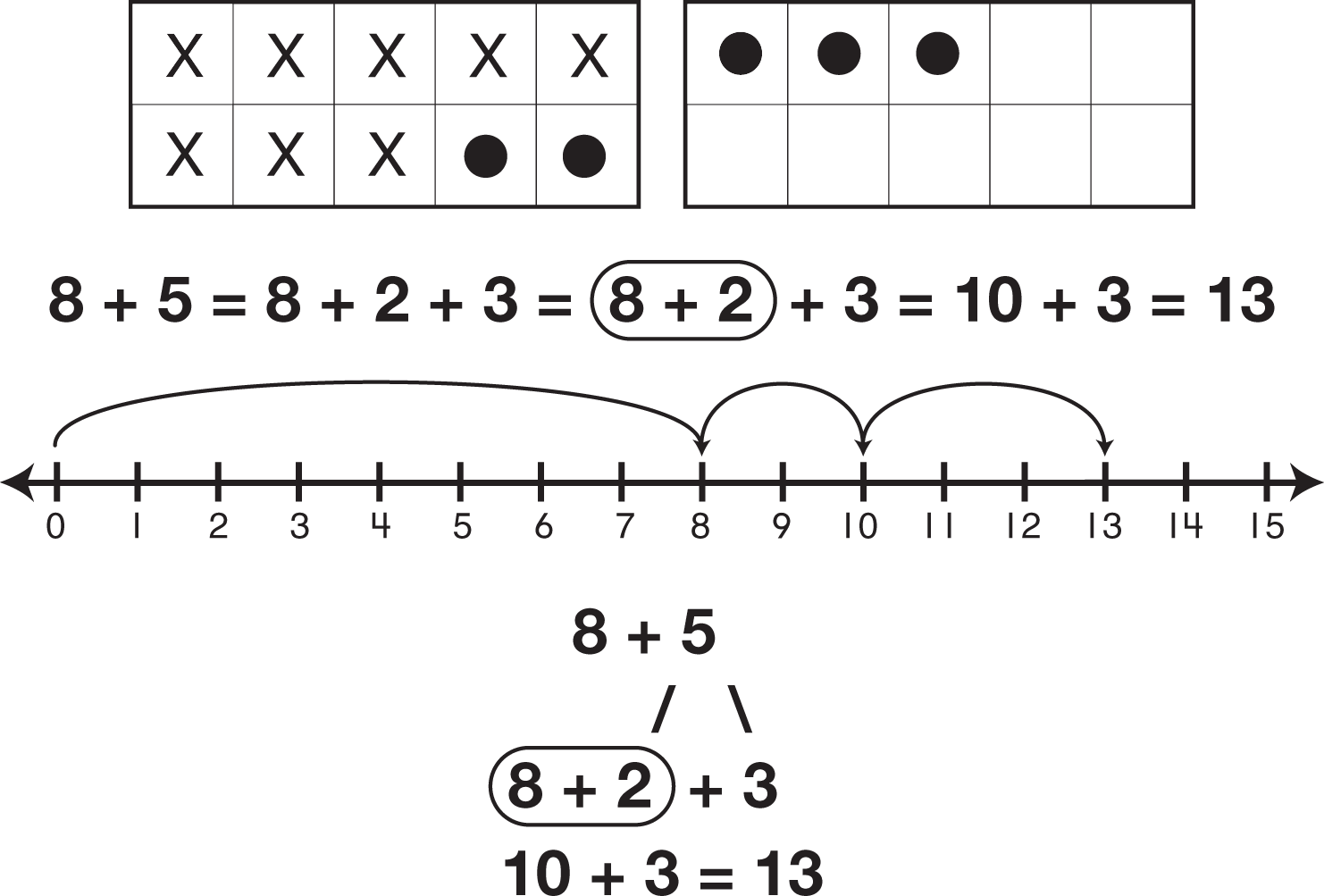
Figure 2: Representations of the making-ten strategy
Subtraction Facts
Like addition, students have continued along the learning progression for subtraction. Students have … read more
Subtraction Facts
Like addition, students have continued along the learning progression for subtraction. Students have been using the relationship between addition and subtraction and counting strategies to solve problems. In this unit, students formalize those counting strategies and develop reasoning strategies. These reasoning strategies are based on the strategies students use for addition. See Figure 3.
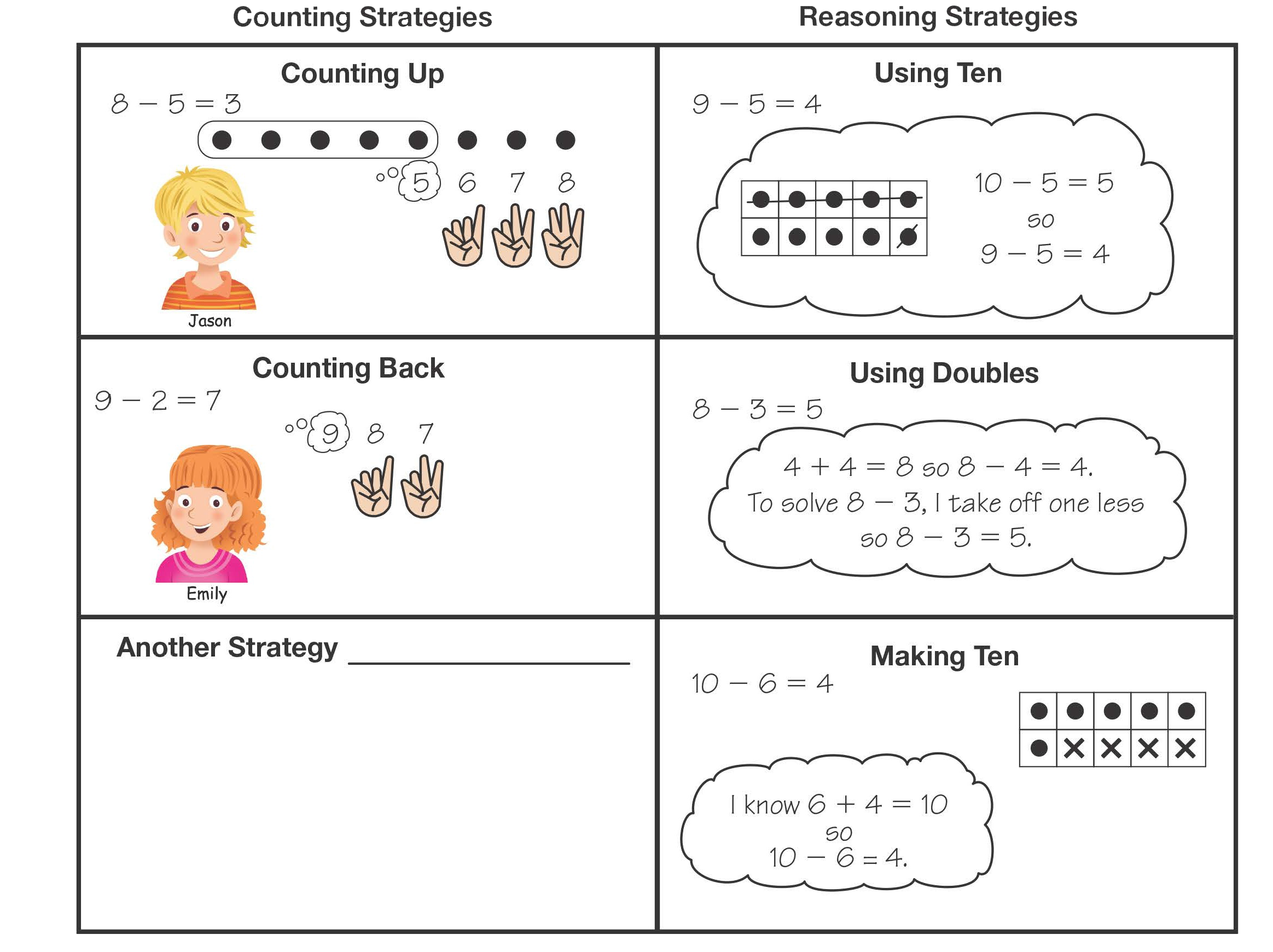
Figure 3: Subtraction Strategies Menu from Lesson 10
MATH FACTS PRACTICE and ASSESSMENT

Practice and assessment of the math facts is based on the results of research in … read more
Practice and assessment of the math facts is based on the results of research in the field. The following paragraph from Adding It Up: Helping Children Learn Mathematics published by the National Research Council summarizes much of the literature on practice:
"Practicing single-digit calculations is essential for developing fluency with them. This practice can occur in many different contexts, including solving word problems. Drill alone does not develop mastery of single-digit combinations. Practice that follows substantial initial experiences that support understanding and emphasize 'thinking strategies' has been shown to improve student achievement with single-digit calculations" (National Research Council, 2001).
Researchers caution that too much drill too soon can have a negative impact on students' acquisition of the math facts. Studies have shown that "premature practice can be detrimental but that properly managed practice is essential in the development of expertise.... Brief, engaging, and purposeful practice distributed over time is usually most effective" (Brownell & Chazal, 1935; Hiebert, 1999; Isaacs & Carroll, 1999).
Following these recommendations, fact practice in Math Trailblazers is characterized by the distributed practice of small groups of facts that lend themselves to specific strategies. Practice and assessment occur after students have had substantial experiences learning the underlying concepts and developing strategies that make sense to them.
MATH FACTS and MENTAL MATH

Addition Facts with Sums to Ten
In this unit, students continue to systematically review the addition facts. Daily Practice and … read more
Addition Facts with Sums to Ten
In this unit, students continue to systematically review the addition facts. Daily Practice and Problem items in this unit can be used to assess students' fluency with the addition facts in Group A. Students should be using counting strategies and applying properties of addition (e.g., turn-around facts, adding zero) to solve these facts.
Fact Families for Addition Facts with Sums to Ten
Students have been connecting addition to subtraction and using the addition facts to solve … read more
Fact Families for Addition Facts with Sums to Ten
Students have been connecting addition to subtraction and using the addition facts to solve subtraction problems since Unit 6. A student proficient with their addition facts can also find the related subtraction facts. Daily Practice and Problem items in this unit can be used to assess students' abilities to name the fact families related to each fact in Group A.
Addition Facts with Sums 11 to 20
Students have been connecting addition to subtraction and using the addition facts to solve … read more
Addition Facts with Sums 11 to 20
In this unit, students continue to develop their own strategies for the addition facts with larger sums. In Grade 1, students are expected to develop reasoning strategies for these facts. Students should be encouraged to use strategies that make sense to them and to continue to seek strategies that are efficient. Students will be expected to have fluency with these facts by the end of Grade 2.
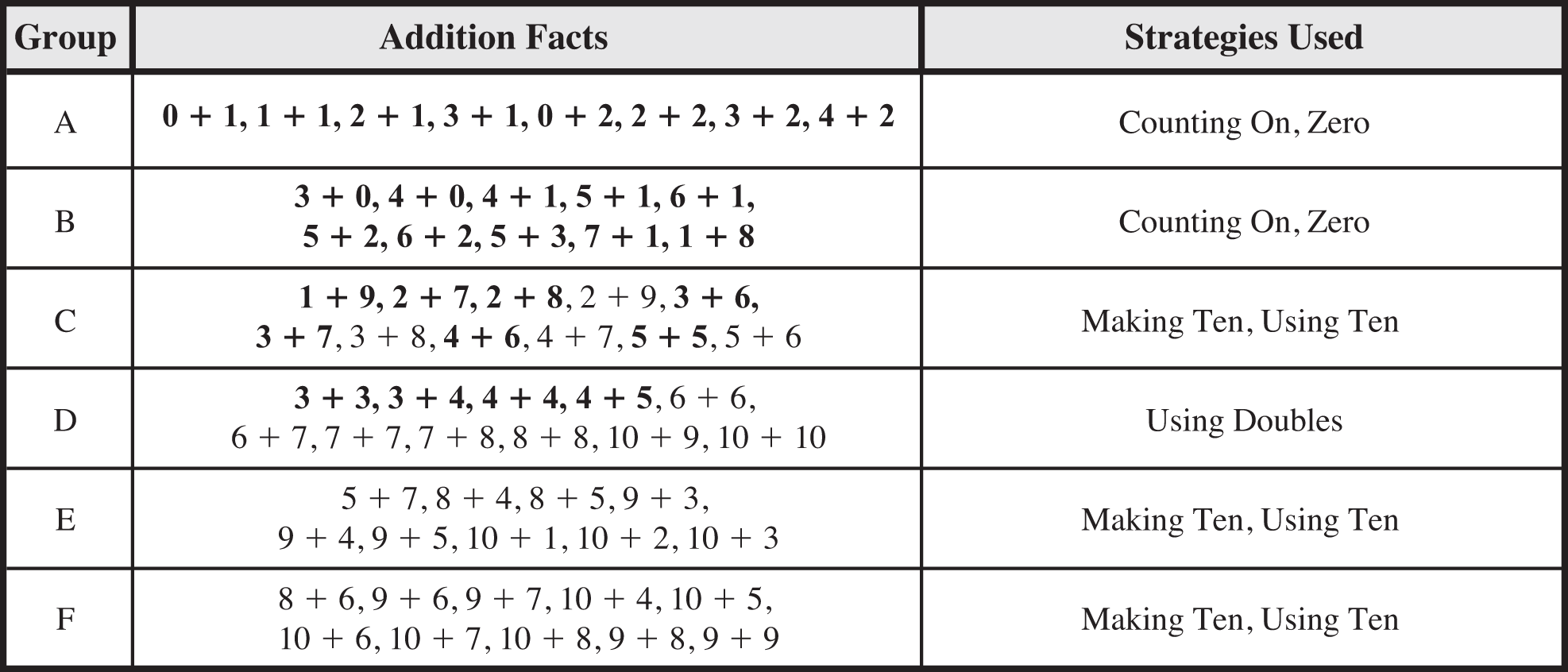
Figure 4: Addition Facts Groups for Grade 1 with sums to ten in bold

Figure 5: Development of addition facts and the related subtraction facts in Grade 1 Units 12–17
Resources
- Baroody, A.J. "Why Children Have Difficulties Mastering the Basic Number Combinations and How to Help Them." Teaching Children Mathematics, 13 (1), 22–31. National Council of Teachers of Mathematics, Reston, VA, 2006.
- Brownell, W.A., and C.B. Chazal. "The Effects of Premature Drill in Third-Grade Arithmetic." Journal of Educational Research,
29 (1), 1935. - Burton, G. M., with A. Mills, C. Lennon, and C. Parker. Number Sense and Operations. Curriculum and Evaluation Standards for School Mathematics Addenda Series, Grades K–6. National Council of Teachers of Mathematics, Reston, VA, 1993.
- Carpenter, T.P., E. Fennema, M.L. Franke, L. Levi, and S.E. Empson. Children's Mathematics: Cognitively Guided Instruction. Heinemann, Portsmouth, NH, 1999.
- Common Core Standards for Mathematics. Council of Chief State School Officers, 2010.
- Curriculum Focal Points for Prekindergarten through Grade 8 Mathematics: A Quest for Coherence. National Council of Teachers of Mathematics, Reston, VA, 2006.
- Fuson, K.C. "Research on Whole Number Addition and Subtraction." In Handbook of Research on Mathematics Teaching and Learning. D. Grouws, ed. Macmillan, New York, 1992.
- Hiebert, James. "Relationships between Research and the NCTM Standards." Journal for Research in Mathematics Education, 30(1), 3–19, National Council of Teachers of Mathematics, Reston, VA, 1999.
- Principles and Standards for School Mathematics. National Council of Teachers of Mathematics, Reston, VA, 2000.
- National Research Council. Adding It Up: Helping Children Learn Mathematics. J. Kilpatrick, J. Swafford and B. Findell, eds. National Academy Press, Washington, DC, 2001.
- Takahashi, A., T. Watanabe, and M. Yoshida. Elementary School Teaching Guide for the Japanese Course of Study: Arithmetic (Grades 1–6). Unofficial translation of Elementary School Teaching Guide: Arithmetic, Japanese Ministry of Education, Culture and Sports, 1989. Global Education Resources, L.L.C., Madison, NJ, 2004.
- Thornton, C.A. "Strategies for the Basic Facts." In Mathematics for the Young Child. J.N. Payne, ed. The National Council of Teachers of Mathematics, Reston, VA, 1990.
- Van de Walle, J.A., and L.H. Lovin. Teaching Student-Centered Mathematics: Grades K–3. Pearson Education, Boston, 2006.












