Big Base-Ten Hoppers

Est. Class Sessions: 2–3

Developing the Lesson

Part 1. Big Base-Ten Hoppers

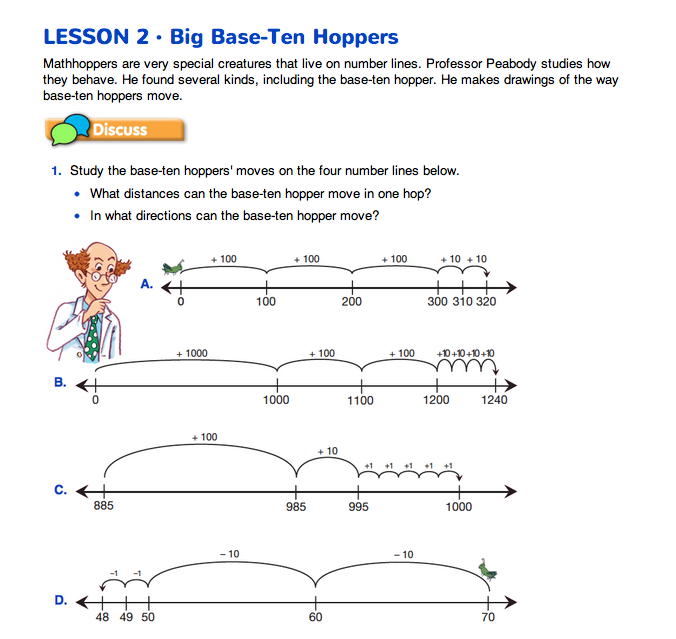
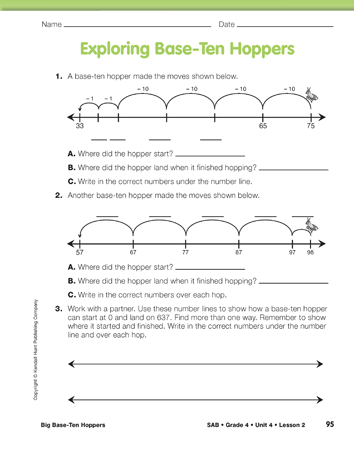
Introduce Base-Ten Hoppers. Use a display of the first Big Base-Ten Hoppers page in the Student Guide to introduce the Base-Ten hoppers. Ask students to work in pairs to study the moves that a Base-Ten hopper can make using Questions 1 and 2. Tell students that they are Professor Peabody's assistants and that they need to prepare an oral report for the rest of the class on their observations of how the base-ten hoppers move and how Professor Peabody records their movements. A possible report follows:

“Base-Ten hoppers can make hops with distances of one, ten, one hundred, and one thousand on number lines. These are the only distances on the four number lines. Base-Ten hoppers can go forward or backward. You can see that sometimes the hoppers go forward and sometimes they go backward. Professor Peabody shows where the hopper lands after each hop by writing the number under the hop. He shows the direction of each hop by writing plus or minus above each hop with how far it goes.”

Encourage those listening to ask questions of those reporting so that everyone understands how the hoppers can move and how to record the movements.

This lesson provides a context for students to develop skills composing and decomposing numbers. Number lines serve as tools for developing mental images of numbers decomposed into groups of ones, tens, hundreds, and thousands. The goal is for students to develop mental math skills that will allow them to use flexible and efficient strategies to estimate, add, and subtract.

For example, to subtract 3001 − 2798, students can count up on a number line that starts at 2798, move forward 2 to 2800, then 200 to 3000, then 1 more to 3001. They add the moves on their hops: 2 + 200 + 1 = 203, so the difference between 2798 and 3001 is 203. They can visualize:

Other students may choose to start at 3001, count back by 100s until they get near the closest hundred, 2801 (3001, 2901, 2801), then count back by ones to 2798 (2800, 2799, 2798). Again, adding the moves on their hops, 100 + 100 + 1 + 2 = 203. Using the number line:

Place the emphasis of this lesson on using number lines to break apart and combine numbers using thousands, hundreds, tens, and ones in flexible and efficient ways and to represent the partitions in number sentences. Focus on supporting this kind of thinking. Students should learn to represent their moves on number lines, so that others can understand their thinking. However, developing consistent notation is not as important as developing flexible thinking.

Use the following prompts to further students' thinking:

How far did the base-ten hopper on Number Line A move? How do you know? (It moved 320. It started at 0 and landed on 320. It made three hops of 100 and two hops of 10. That's the same as 320.)
Write a number sentence to show how the hopper moved on Number Line A. (100 + 100 + 100 + 10 + 10 = 320)
How far did the base-ten hopper on Number Line B move? Write a number sentence that shows how it moved. (1240; 1000 + 100 + 100 + 10 + 10 + 10 + 10 = 1240.)
Write 1240 in expanded form. (1240 = 1000 + 200 + 40)
How is showing the base-ten hopper's moves like using expanded form? How is it different? (Expanded form breaks numbers down into numbers that are in the thousands, hundreds, tens, and ones places. The base-ten hoppers are different because they can also go backward. Also, to record each of the base-ten hopper's hops [one hop of 1000, two hops of 100, four hops of 10], you write 1000 + 100 + 100 + 10 + 10 + 10 + 10 = 1240.)
Where did the base-ten hopper on Number Line C start? Where did it land after its last hop? (It started at 885 and ended up at 1000.)
How far is it from where the base-ten hopper on Number Line C started to where it landed? How do you know? (Possible response: It is 115. It made one hop of 100, one hop of 10 and 5 hops of 1.)
Describe how the base-ten hopper moved on Number Line D. (Possible response: It started at 70. It moved back ten twice, then back one twice, and it ended on 48.)
How far did it move? How do you know? (It moved back 22. Possible response: Two tens and two ones make 22.)

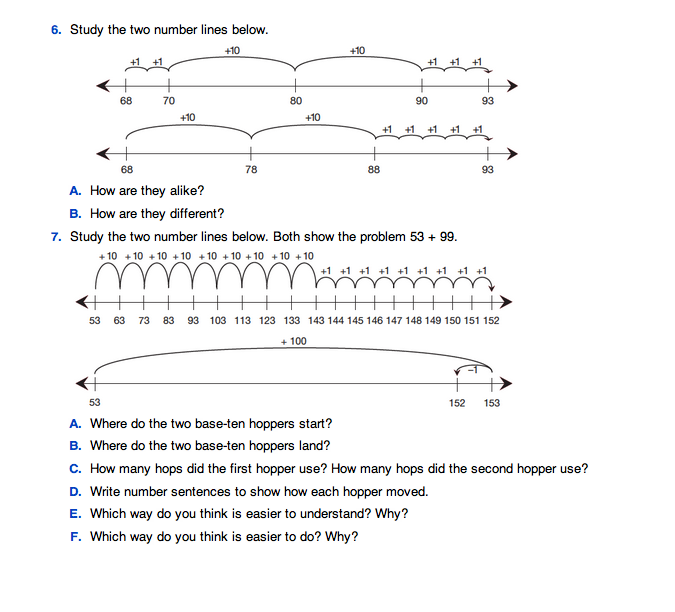
Show Hops on the Number Line. Ask students to work on Questions 3–8 in pairs. These questions help students understand how they can show moves on the number line so someone else can see where the hopper starts, the distance and direction of each move, and the final stopping point.

Question 6 shows two ways to start at 68 and move forward 25. Students first compare the two sets of moves. The first hopper decides to partition the 5 into 2 and 3, so that it can move forward two from 68 to get to the nearest ten (68, 69, 70). Then it can hop two tens on the tens (80, 90) and then hop the last three ones (91, 92, 93) to 93. The second hopper starts counting by tens right away and then counts on the 5 ones (68, 78, 88, 89, 90, 91, 92, 93).

Ask:

Which of the two ways the hopper moved from 68 to 93 in Question 6 is easier for you? Why?

In Question 7, students are introduced to base-ten hoppers that change direction in order to move to a target number in a more efficient way. For example, the number lines show moves adding 53 + 99. The first example shows partitioning 99 into 90 + 9 and making nine hops of 10 and nine hops of 1. The second example uses the fact that 99 is just 1 less than 100. The hopper makes one forward hop of 100, then one hop backward of 1. Students should see that both are appropriate ways to solve the same problem but that one is more laborious. Check for understanding in the second example. Ask a volunteer to write number sentences on the board for Question 7D.

53 + 90 + 9 = 152
53 + 100 − 1 = 152

Ask:

Which of these sentences is a true sentence? Why? (Both are true; 90 + 9 is the same as 99 and 100 − 1 is the same as 99. Both sides of both sentences add up to 152.)

Students may recall making similar kinds of moves on their 100 Charts and 200 Charts in earlier grades. For example, on the 100 Chart, to add 22 + 19, they could start on 22 and move ahead two rows (of 10) to 42, and then back 1 space to 41. Discuss student responses to Questions 7E and 7F.

Question 8 draws attention to a common misreading of a problem, that is, differentiating between a problem that says “move back 200” and one that says “move back to 200.” Help students recognize the semantic difference between the two and the necessity of reading a problem carefully.

Students may complain of tedium in drawing and labeling each move, such as multiple hops of 10 as in Question 7. If so, tell them the 9 hops of ten can be written as one hop of 90, because 90 is a multiple of 10.

Explore Base-Ten Hoppers. Have students complete the Exploring Base-Ten Hoppers pages in the Student Activity Book. Remind them again to read the problems carefully, noting the difference between “move back” and “move back to.”

Several questions ask students to find more than one way to show how a hopper can move various distances on number lines. Ask more than one pair of students to draw their number lines and hops for each question on the board. Then ask other students to describe the moves shown on the board. Encourage them to question the students who presented their number lines if the moves are not clear or correct. Ask students who drew the number lines to explain why they chose to make the moves they did.

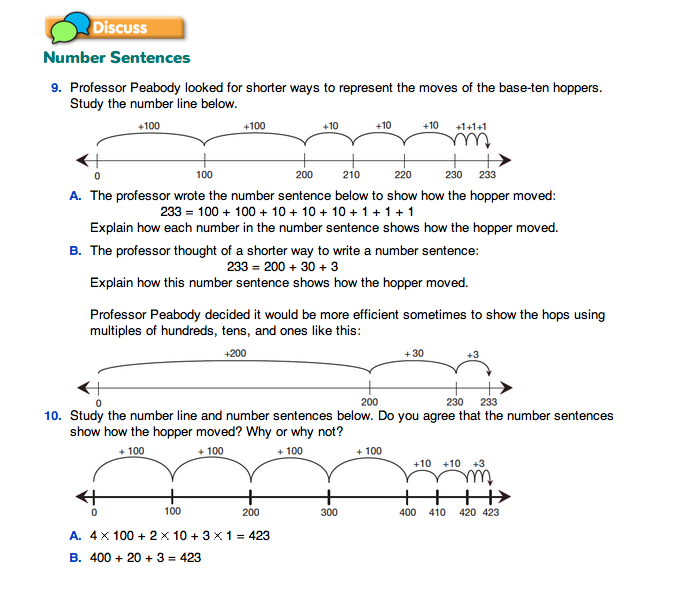
Number Sentences. The Number Sentences section in the Student Guide discusses how to show moves on number lines with number sentences. Have students discuss Questions 9–10 in pairs, then as a class. Have them connect each hop on the number lines to the symbols in the number sentences.

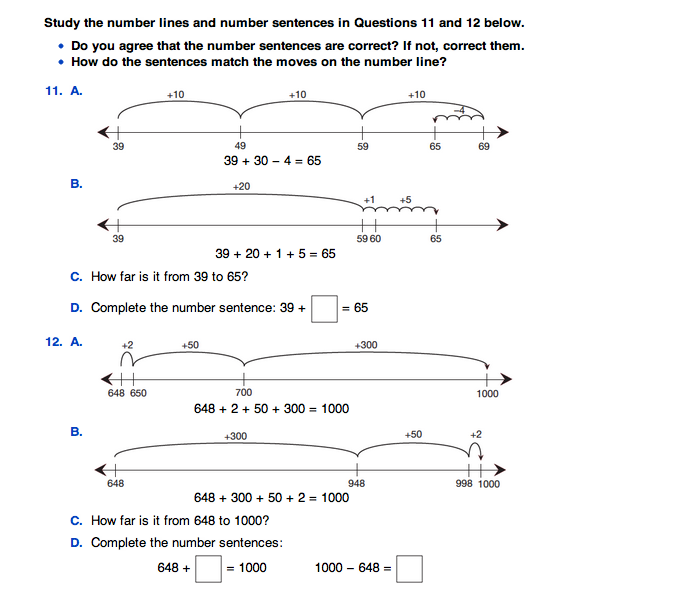
Questions 11–12 develop the idea of using number lines to find the difference between two numbers. That is, finding how far it is from 39 to 65 on a number line is the same as subtracting 39 from 65 and counting up from 39 to find the difference. Ask students to match the moves on the number lines to the numbers in the sentences.

After students have completed Questions 11D and 12D, ask:

We can use the number line to write a “family” of addition and subtraction number sentences like fact families. What three number sentences are related to 39 + 26 = 65? (26 + 39 = 65, 65 − 39 = 26, 65 − 39 = 26)
What are the four number sentences related to the hops on the number line in Question 12D? (648 + 352 = 1000, 1000 − 648 = 352, 352 + 648 = 1000, 1000 − 352 = 648)

Ask volunteers to write the sentences on the board.

Show where each number in each number sentence is on the number line.

Check-In: Questions 13–19 provide more practice using number lines to partition numbers and to count up and count back on number lines. If appropriate, use these questions to assess students' initial grasp of the use of partitions of a number to add and subtract on the number line. Alternatively, assign these questions for homework.

Use Check-In: Questions 13–19 to assess students' abilities to represent and solve addition problems using number lines [E2] and to represent and solve subtraction problems using number lines [E3].

Activities in Lesson 3 and Lesson 7 provide targeted practice.