Teacher: Let's talk about our strategies for placing the digits where we did. First, when subtracting, do you have to think about anything different than when adding?
John: Yes, the top number has to be bigger than the bottom number, or else you can't subtract. The answer would go below zero.
Teacher: That's right, John, you would have a negative number for your answer and we're not dealing with negative numbers yet. For this game you would have already lost, because you wouldn't be able to subtract your bottom number from your top. So what do you do to make sure you can subtract, Lee Yah?
Lee Yah: If I get a large number I better put it in the top number.
Teacher: Where in the top number, which place?
Lee Yah: I think just any place.
Teacher: Keenya, you look like you don't agree. What do you think?
Keenya: No, I don't agree. You'd have to put it in the hundreds place to make it a big number. If you put it in either of the other two places, you might have to put a little number in the hundreds place and that would make it a small number.
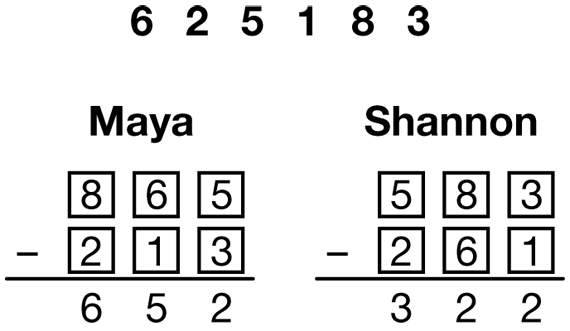
Teacher: That's right, Keenya. It is the hundreds place that matters first, isn't it? Now, looking at Maya's and Shannon's game boards, I notice that both girls placed the first number 6, in the tens place. Maya placed it in the top number and Shannon placed it in the bottom number. Can you each explain your thinking?
Maya: Six is kind of a middle-sized number so I put it in the middle. I was hoping I would get a bigger number for the hundreds place.
Shannon: I thought it was a middle-sized number too, but it seemed that there would be bigger numbers called later, so I put it in the bottom number. But I think I should have put it on top someplace like Maya.
Teacher: Why do you think that?
Shannon: Well, I wasn't thinking of it as being big, but it really is kind of big, and there aren't very many numbers bigger. Only, 7, 8, 9. And there are 0, 1, 2, 3, 4, and 5 that are littler. So if I wanted a big difference, I should have put it on top.
Teacher: That's good reasoning, Shannon, but it's sometimes hard to think that clearly when you are in the middle of a game, isn't it?
Shannon: Yes, I wish I had thought about it then.
Teacher: Now, you both put 2, which was the next number, in the 100s place of the bottom number. Can you explain why?
Shannon: I know 2 is a little number and the hundred in the bottom number has to be a little one. So I put it there.
Maya: That's the same thing I thought.
Teacher: Why does the number in the hundreds place of the bottom number have to be little?
Maya: Because you are subtracting it. It can't be bigger than the hundred in the top number. And we wanted to get the biggest difference we could, so we would want to make sure it is a small number, not a middle-sized one.
. . .
Teacher: Was anyone able to solve their problem using mental math?
Maya: Mine was almost like mental math. I didn't have to make any trades or borrow or write anything down. All my top numbers were bigger than the bottom numbers so it was real easy.
Jerome: That's how mine was, too.
Jessie: Mine was like that too, but I didn't notice it at first, so I did the expanded form.
Teacher: What was your problem, Jessie? Can you show us how you solved it on the board?