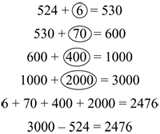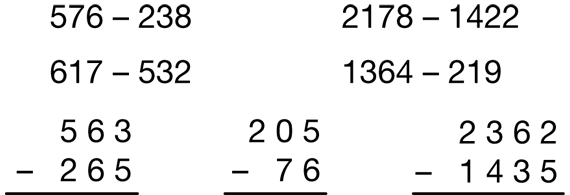Solving Problems with No Trades. To review how to use and record base-ten pieces, start with problems that do not involve trades. Ask volunteers to show their solutions on the board as the other students solve the problems with their own pieces. If you have enough pieces, it is good for each student to work with his or her own.
Introduce the problem by telling the students:
- The TIMS Candy Company sells candy at the factory store. The store starts each day with 576 Chocos.
Use base-ten pieces or shorthand to show 576 Chocos. Check to see that students have represented 576. Most students will represent 576 using the fewest pieces, though students would not have to.
Tell students the next part of the problem:
- On Monday, the store sold 241 Chocos. How many Chocos are left at the store?
Tell students to use their base-ten pieces or shorthand to take 241 Chocos away from the 576 Chocos. See Figure 2. After students have had a chance to remove 241 Chocos, ask students to figure out how many pieces are left. There are 335 Chocos left in the store on Monday.
- Is your answer reasonable? How do you know? (Students could estimate by thinking about base-ten pieces; 500 − 200 = 300 which is close to 335.)
Ask students to solve this problem:
- At the end of the day Tuesday, there are 465 Chocos left in the store. If the store started the day with 576 Chocos, how many Chocos were sold on Tuesday?
Modeling Subtraction with Base-Ten Pieces. There is a fundamental difference between modeling addition with base-ten pieces and modeling subtraction. When modeling addition, you begin by putting down pieces to represent each number you are adding (the addends). But when modeling subtraction, you put down pieces that represent only the first number in the problem (the minuend). You then show subtraction by taking away pieces that represent the second number (the subtrahend). See Figure 2. As students work with the pieces, be sure they do not begin the problem by laying out pieces for both numbers.
Ask students to use the base-ten pieces to show 576 and then take away 465. After students have had a chance to solve the problem using base-ten pieces, ask a student to share his or her solution. While the student is sharing the solution, record the corresponding steps on a display of a Base-Ten Recording Sheet. See Figure 3.
- How do you show 576 on the recording sheet? (See Figure 3.)
- What pieces will you take away? (465)
- How many Chocos were sold on Tuesday? (111)
- How did you figure that out? (Possible response: I counted the pieces left after I took away 465 pieces.)
- How can you check your answer? (Possible response: Add 465 to 111 and I should get 576. I do, so 111 is correct.)
Figure 4 shows several more problems that do not involve trades. As needed, ask students to solve them with base-ten pieces or with base-ten shorthand and to record their work on a copy of the Base-Ten Recording Sheet Master.
- How could you do the last problem in your head? (Since 402 is 2 more than 400, the 400 can be subtracted from 1506 giving 1106. Then, taking away 2 more leaves 1104.)
- Is this problem similar to one on our chart paper?
- Did you use the same strategy or a different strategy?
Solving Problems with Trades. After solving a few problems that do not involve trading, students can solve problems that involve trading.
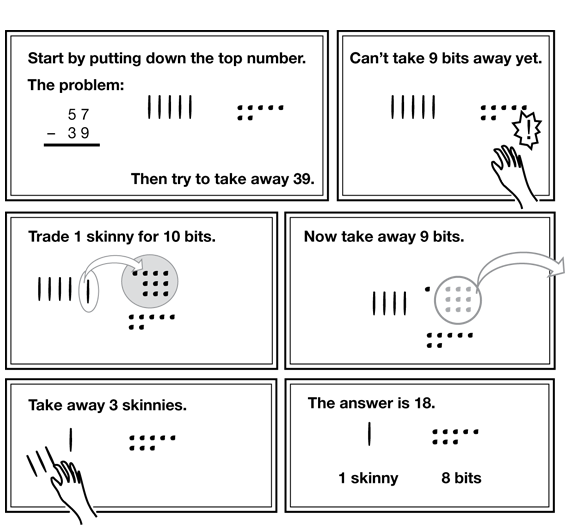
- At the beginning of the day, there were 57 Chocos at the TIMS Candy Company. Customers bought 39. How many were left?
This problem is shown in Figure 5 and Figure 6. As students work on the problem, circulate and see how they are dealing with the need to trade. If there are several groups that do not know what to do, then you can work together as a class to solve the problem. Otherwise, let students talk in their groups. Then ask students to present their work on the board.
As students show their work with the pieces, check for their understanding of trading. Make sure they understand that trading does not change the value of the number. It just changes the way it is partitioned. Students should record the new partitions on the recording sheet.
Model a few more problems that involve trading, such as the problems in Figure 7.
- When you solved 73 − 28, did you make any trades? (Yes. I traded one of the 7 skinnies for 10 bits.)
- Did that trade change the value of the number 73? (No. It just gave me 6 skinnies and 13 bits so I could take 8 bits away.)

As students work with the pieces, use prompts similar to those below to help individual students make connections between the representations with base-ten pieces and what they write using numbers. The questions and answers below use 1364 − 219 as an example and assume that students have a “bank,” a “work pile,” and a “take-away pile” as described in the TIMS Tip at the beginning of Part 1.
- Which number do you represent with base-ten pieces in your work pile first? How? (1364; I put down 1 pack, 3 flats, 6 skinnies, and 4 bits.)
- What do you write on the recording sheet? Where will you put each number? (1364; I put the 1 in the thousands place, the 3 in the hundreds place, the 6 in the tens place, and the 4 in the ones place.)
- How will you show that you are subtracting 219 with the pieces? (I have to take away 2 flats, 1 skinny, and 9 bits.)
- Do you take those pieces out of the bank and show them in your work pile? (No, I just take them away from what is already in the work pile and put them in the take-away pile.)
- How do you show what you are going to take away on the recording sheet? (I write − 219 underneath.)
- Do you have to make any trades to take away 219? (I need to take away 9 bits, but I have only 4 on my desk. So, I need to trade 1 skinny for ten bits.)
- Where do you get the bits? What will you do with the skinny? (I go to the bank. I put the skinny in the bank and I trade for 10 bits.)
- What pieces do you have in your work pile now? (1 pack, 3 flats, 5 skinnies, and 14 bits)
- Have you changed the value of the number in your work pile? What is the number that these pieces represent? Show me with the pieces. (1 pack, 3 flats, and 5 skinnies is 1350. Add on 10 bits and that is 1360. 4 more bits is 1364. That is the number I have to subtract from. See it is right there on my recording sheet.)
- How do you represent the trades on the recording sheet? (I rewrite 1364 as 1 pack, 3 flats, 5 skinnies, and 14 bits.)
- What does the 5 tell you now? What column is the 5 in? (That I have 5 skinnies. It is in the tens column.)
- Can you subtract 219 from that now? Show me. [Takes away 9 bits, 1 skinny, and 2 flats.]
- What pieces are left in your work pile? (I have 1 pack, 1 flat, 4 skinnies, 5 bits.)
- What number do your remaining pieces represent? Where will you write that on your recording sheet? (1145. I draw a line under 219 and write 1145 under that.)
- How many pieces are in your take-away pile? (219)
- If you put them together with the pieces in your work pile, what pieces will you have altogether? What number will they represent? Show me. (They represent 1364. That's the number I started with.)
As you discuss the steps, ask questions that will check students' understanding of the connection between the trades you made with the pieces and the marks you made in the table. After making and recording the trades, complete the subtraction problem and write the answer.
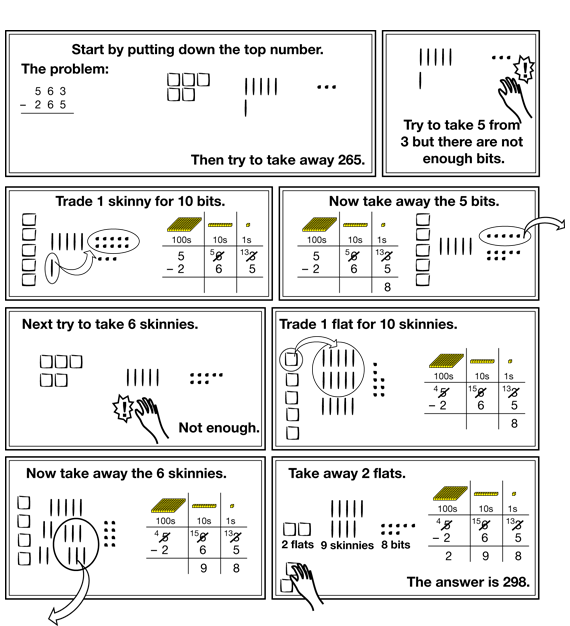
Figures 8 and 9 show how to solve a subtraction problem with more than one trade, 563 − 265. Ask students to solve them with partners using their base-ten pieces and to record their trades on a Base-Ten Recording Sheet using numbers. Students need not record their trades using base-ten shorthand. However, it is important for students to think through the process for themselves using the pieces. They need to take time to make connections between the quantities and trades represented by the pieces and the quantities and trades they record using symbols on the recording sheets.
Once students have solved the problems in Figure 10, ask students to share a few solutions. Students may need help recording and keeping track of more than one trade.
Once you have shared a few examples, ask:
- How are you keeping track of trades on the recording sheet?
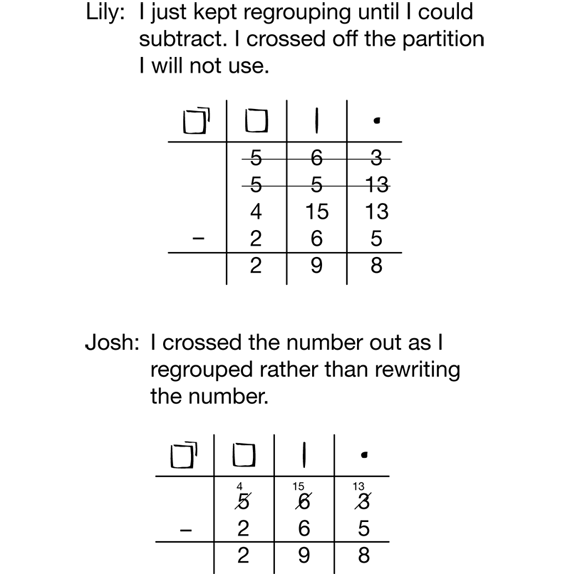
Show students some of the ways they can record trades on the recording sheet. In Figure 9, Lily shows how to rewrite the number using different partitions. Students should be familiar with this notation from previous work in Grade 3. Notice how she crossed off the number partition she is no longer using. Josh, in Figure 9, shows how he crossed out the numbers and made notes above the numbers. Let students choose whichever notation is easier for them. If students are having trouble keeping track of trades, encourage them to use Lily's notation. There is less room for error and it is easier to check their work as trades are made.
A Good Problem for a Mental Math Strategy.
Referring to the problems students just solved, ask:
- What are some advantages of the base-ten pieces? How do they help us solve problems? (You can see the trades and make the trades for real. I also then check the numbers I write down.)
- What are some disadvantages of the base-ten pieces? (You cannot carry pieces with you and sometimes I get them mixed up.)
- Do you think a mental math strategy would be more efficient for any of these?
- What mental math strategy would you use?
Encourage students to explain their choice of problem and mental math strategy. Students could choose from the class collection created in Part 1 or choose a new strategy to add to the collection.
For example, they can count up as shown below and in Figure 11 on a number line:
4 + 20 + 100 + 5 = 129
Figure 12 shows more subtraction problems that can be solved in small groups. The amount of guidance and practice needed will depend on students' experiences.
If students are comfortable with the traditional algorithm, they can solve problems on their own paper instead of on the Base-Ten Recording Sheet. Be sure they understand that the place values in a number give the same information (ones, tens, hundreds, etc.) as the columns on the recording sheet.
Note that the last three problems in Figure 12 involve regrouping several times. Students often have trouble with problems such as the last one, 3000 − 524. Point out that the problems can be done by alternative methods that may be more efficient.
- What different strategies can you use to solve 3000 − 524?
For example, 3000 − 524 can be solved by first doing 2999 − 524 and then adding 1 to the answer. Using this method, no regrouping is required. 3000 − 524 can also be done mentally by counting up:
Have students write their strategies on chart paper and add to the class collection created at the beginning of this lesson.