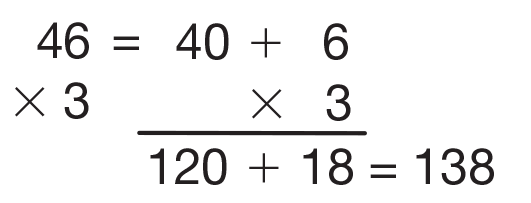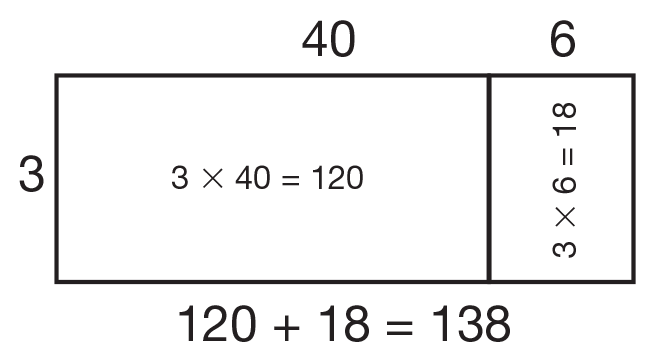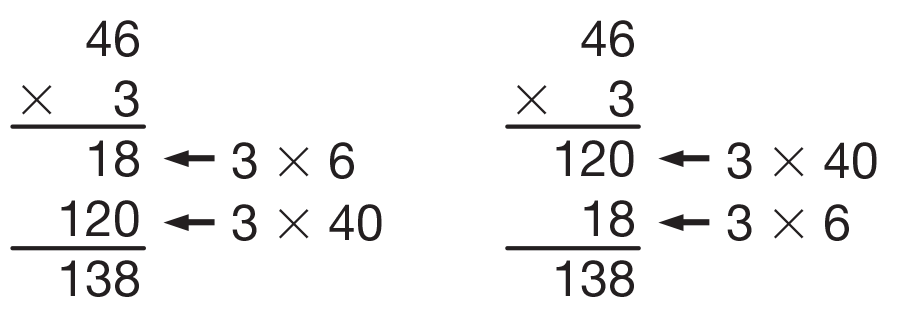Lesson 9

Paper-and-Pencil Multiplication

Est. Class Sessions: 2–3

Developing the Lesson

Part 1. The All-Partials Method

Review multiplication using expanded form and rectangles from Lesson 8. Ask students to work in pairs to solve 46 × 3. Ask them to choose one student to use expanded form and the other to use rectangles. They can use the examples on chart paper from Lesson 8 or Nila's and Sara's methods in the Discuss section of the Student Guide for Lesson 8. Ask one pair to display their solutions for the class. See Figures 1 and 2.

Ask:

X
  • How are these methods similar? (The numbers are broken into groups of tens and ones, and then the partial products are found and added together.)
  • How are they different? (Sara uses a rectangle and number sentences to keep track of what she is doing, and Nila uses just number sentences.)

Ask students to study the examples on the first Paper-and-Pencil Multiplication page in the Student Guide. The first shows 46 × 3 using expanded form and the next two examples show
46 × 3 using the all-partials method. Ask students to discuss Questions 1–3 in pairs before discussing them with the class.

In the all-partials method, students write down all of the products and then add. Ask students to look at the problem
46 × 3 as it is solved in the Student Guide and to explain the meaning of each of the numbers in the solution. Write a multiplication expression beside the numbers as in Figure 3 to show how the partial products are computed. Note that it does not matter which order the products are recorded.

Ask:

X
  • Should we add the all-partials method to our collection of strategies?

Ask students to try this strategy to solve 83 × 6. Ask a student to record the solution on chart paper. Title the strategy “all-partials.” Display this chart with the other strategies discussed in Lesson 8.

Ask:

X
  • Compare the all-partials method to Sara's method (rectangle) and Nila's method (expanded form). How are they similar? (The numbers are broken into groups of tens and ones; the partial products are found and recorded and then added together.)
  • How are they different? (In all-partials, just the partial products are recorded, not the related number sentences; the partial products are recorded vertically.)
  • Which method do you like better?

To probe students' understanding of the all-partials method, ask:

X
  • In the problem 83 x 6, why did we write 480? Since 6 x 8 = 48, why didn't we write 48 on the second line? (Because we are multiplying 6 times 8 tens, not 6 times 8 ones.)
  • Some people like to multiply the ones first; others multiply the tens first. Does it matter? (No, you get the same answer either way.)

When you feel students are ready, ask them to solve the problems in Questions 4–7. They can compare their answers with a partner and discuss any discrepancies.

Student Guide: 158 159
Answers
X
SG_Mini
+
X
SG_Mini
+
Student Activity Book:
Master:
Using expanded form
X
figure 1
+
Using rectangles
X
figure 2
+
Order does not matter when multiplying using the all-partials method
X
figure 3
+