Use resealable plastic bags or shoe boxes to store the sets of base-ten pieces. Pieces not in use should be kept in the storage containers.
Review Base-Ten Pieces. You may go through the material quickly if your class has previously worked with base-ten pieces. However, most students benefit from a review. Be sure to review the following terms at the appropriate time:
- The Base-Ten Recording Sheet is where numbers are recorded in writing in base-ten partitions.
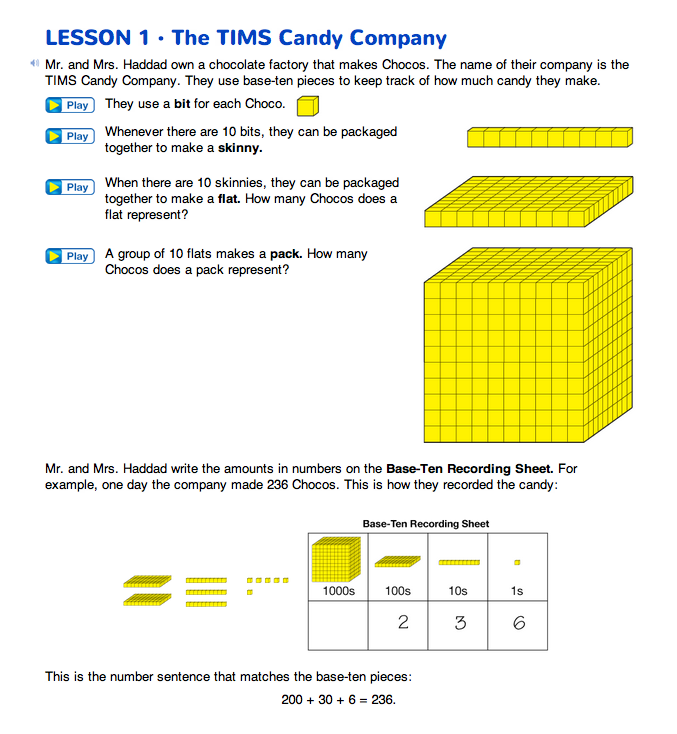
- Individual cubes are called bits. When 10 bits are put together, they form a skinny. Ten skinnies form a flat, and ten flats form a pack.
- The Fewest Pieces Rule means that we want to represent quantities using the fewest number of base-ten pieces possible, that is, using fewer than 10 pieces in any place-value column.
If students hesitate when trading with the base-ten pieces, ask students to build a skinny from 10 bits, a flat from 10 skinnies, and a pack from ten flats.
At appropriate points during the lesson, you may wish to refer to the bits as ones, skinnies as tens, flats as hundreds, and packs as thousands. However, when studying decimals in Grades 3 and 4, we will assign other values to the pieces. For example, the flat will be the unit. Then the skinny is .1 (one-tenth) and the bit is .01 (one-hundredth).
Students who need more practice representing numbers with base-ten pieces can play Make a Pack using copies of the Make a Pack and Make a Pack Game Board Masters in the Teacher Guide.
Have students read the opening vignette on The TIMS Candy Company pages. Explain that the TIMS Candy Company uses base-ten pieces to keep track of the candy. Whenever they have ten bits, they can trade them for a skinny. Ten skinnies can be traded for a flat. When needed, they can also trade in the other direction; e.g., they can trade a skinny for ten bits.
During the class discussion in Part 1 of this lesson, pay attention to how well students are able to see that the number represented with base-ten pieces remains the same after trades are made [E1]. Make notes on the Unit 4 Assessment Record.
Activities in Lesson 3 and 7 and the Make a Pack game provide targeted practice.
Ask a student to take a handful of bits (between 20 and 40) and display them for the class to see. Ask a volunteer to tell you how many Chocos they represent and write the total in the bits column on the display of the Base-Ten Recording Sheet from the Teacher Guide. Have students take out the same number of bits and write the number in the bits column on a Base-Ten Recording Sheet.
- How many “ones” are shown on the recording sheet?
- What trades can we make?
Give students time to decide for themselves how to make trades with their pieces. After the class has made trades using their pieces, ask a student to show one trade. For example, with 27 bits, trade 10 bits for a skinny. Model it on the display of the Base-Ten Recording Sheet by drawing a line under the 27, and writing in a “1” for the new number of skinnies and 17 for the bits as shown in Figure 1.
- If a bit represents a one, what does a skinny represent? (ten)
- How many tens do we have now? (one) How many ones do we have? (17)
Write the number sentence 10 + 17 = 27 on the recording sheet display as shown in Figure 1.
- Is this a true number sentence? How do you know? (Yes, it is true. I can count up one 10 from 17 and get 27.)
- How do you know using our base-ten pieces? (We have a skinny, which is ten, and 17 bits, which are ones. 10 + 17 is 27.)
- When we trade 27 bits for 1 skinny and 17 bits, do they still represent the same number (of Chocos)? (Yes, 27 bits represents the same number that 1 skinny and 17 bits does—27.)
Stress to students that the total number (27) is still the same even though a trade has been made.
Ask a student to show another trade and record it on the display of the Base-Ten Recording Sheet as in Figure 1.
- What number sentence now describes our base-ten pieces? (20 + 7 = 27)
- Is this a true number sentence? (Yes)
- How does this number sentence match our new base-ten pieces? (The 20 is 2 tens, which is 2 skinnies. The 7 is for the 7 ones, which is the 7 bits. The 27 tells how much we have altogether.)
Write 20 + 7 = 10 + 17 on the board.
- Is this sentence true or false? How do you know? (It is true; both sides are equal to 27.)
Ask students to work in pairs to partition 35 bits in as many ways as possible and to record their partitions using number sentences. See Figure 2.
Hundreds, Tens, and Ones. Explain to the class that for the TIMS Candy Company to operate as efficiently as possible, it decided that ten skinnies should form a new piece called a flat. Ask students to place ten skinnies side–by–side to show that this group of pieces is exactly the same size as a flat.
- How many bits are in a flat? (100 bits)
Have students skip count by tens to 100 with their pieces. When they have 10 skinnies, these can be exchanged for a flat.
- Take out 3 flats.
- How many skinnies will there be if these flats are broken up? How do you know? Show your partner with the pieces. (3 flats is the same as 30 skinnies.)
- How many bits are the same as 3 flats? How do you know? (1 flat is 100 bits, so 3 flats is 300 bits.)
Give each student 3 or 4 copies of the Base-Ten Recording Sheet Master from the Teacher Guide. Have students use the pieces to complete several more examples like this as needed.
- Take out 2 flats, 6 skinnies, and 4 bits.
Ask them to record the pieces on a Base-Ten Recording Sheet in the appropriate columns. See the first row in Figure 3.
- What number sentence can we write that matches these Base-Ten pieces? (200 + 60 + 4 = 264)
- Talk with your partner and show how each number in the sentence is represented by the pieces. (The 200 is the 2 flats; each flat is one hundred, so we have 2 hundreds. The 60 is the 6 skinnies; each skinny is ten, so we have 6 tens. The 4 is 4 bits; each bit is one, so it is 4 ones.)
- How many bits would there be if the flats and skinnies were broken up and they were all in the bits column? (264 bits)
- Work together with your partner to show another way to partition 264 using base-ten pieces. Write a number sentence to show this partition.
Have a student pair record their partition of 264 on the display of the Base-Ten Recording Sheet. One possible student response is: 2 flats, 5 skinnies, 14 bits. See Figure 3.
- Is this the same number as we had before? Does it represent the same number of Chocos? (Yes.)
- How do you know? (We made an equal trade but we didn't change it in any other way.)
- What number sentence matches these pieces? (200 + 50 + 14 = 264)
Write the following sentence on the board or overhead: 200 + 50 + 14 = 200 + 60 + 4
- Is this a true or a false statement? (It is true.)
- How do you know it is true? (If you add the two sides of the equal sign, you get the same number on each side, 264.)
- How do you know it is true using our collection of Base-Ten pieces?(We just traded one skinny for 10 bits. It was an equal trade, so it is still the same.)

If some or all of your students are unable to write a correct number sentence to represent a grouping of base-ten pieces, provide additional practice using the problems below. Have students build the groupings with their base-ten pieces first. Remind them to skip count by tens to get the totals for the skinnies, particularly if they are having difficulty translating to numbers; for example, translating between 15 skinnies and the number 150.
- 8 skinnies and 6 bits
- 1 flat, 4 skinnies, and 3 bits
- 1 flat, 10 skinnies, and 7 bits
- 1 flat, 12 skinnies, and 9 bits
- 1 flat, 5 skinnies, and 15 bits
- 1 flat, 8 skinnies and 20 bits
- 2 flats, 22 skinnies, and 6 bits
- 4 flats, 15 skinnies, and 12 bits
Using the Chocos context may help some students understand that the different partitions represent the same number.
Ask:
- How many Chocos do the base-ten pieces represent?
Ask students to use their pieces to find three other partitions of 264 and record them on their recording sheets. See Figure 3 for possible partitions.
Reinforce with students that each representation and its descriptive number sentence represents the same number. Repeat with other three-digit numbers as needed.
Thousands, Hundreds, Tens, and Ones. Once the class is familiar with the flats, introduce the packs as 10 flats. Ask students to make a pack by stacking flats atop one another. Have students count by 100s to 1000 to determine how many bits there are in a pack.
- How many bits in one flat? (100 bits)
- Let's count together as you stack the flats to make a pack. (100, 200 … 1000)
- How many bits in a pack? (1000 bits)
- How many skinnies in one flat? (10 skinnies)
- Let's count with the flats again, this time thinking about skinnies. (10 skinnies in one flat, 20 skinnies in two flats … 100 skinnies in 10 flats)
- How many skinnies in one pack? (100 skinnies)
- How many tens in 1000? (100)
- How many bits in one skinny? (10 bits)
- One hundred skinnies in one pack and 10 bits in each skinny, so what is 10 times 100? (1000)
Hold up a pack and tell the students that one of your former students thought there were 600 bits in a pack.
- Why do you think he thought there were 600 bits in a pack? (Maybe because the pack has 6 faces and he could see 100 bits on each face.)
- What would you tell my student?
Ask a student volunteer to role-play how to explain to your former student what the correct number of bits in a flat is. Suggest he or she use Base-Ten pieces to demonstrate.
- Take out 1 pack, 3 flats, 7 skinnies, and 6 bits.
Ask them to record the pieces in the columns on their Base-Ten Recording Sheet and to write a number sentence that reflects the Base-Ten pieces. Ask a student to complete the display of the Base-Ten Recording Sheet for this number. See Figure 4.
- What is a number sentence for these pieces? (1000 + 300 + 70 + 6 = 1376)
- How many thousands are in the thousands column? (1 thousand)
- How many hundreds are in the hundreds column? (3 hundreds)
- How many tens in the tens column? (7 tens)
- How many ones in the ones column? (6 ones)
- Use the pieces to partition 1376 in two more ways and show the partitions on your recording sheets. (Possible partitions are shown in Figure 4.)
- Write true number sentences using different partitions on each side of the equal sign.
Possible sentences are shown below:
1000 + 300 + 70 + 6 = 1300 + 70 + 6
1300 + 70 + 6 = 1000 + 300 + 60 + 17
- Take out 2 packs, 4 flats, and 9 skinnies.
Again, ask them to fill in the Base-Ten Recording Sheet and write a number sentence. Ask questions, drawing attention to the fact that there are zero tens, so the number zero must be written in the tens place.
- How do we write the number? How many Chocos do the pieces represent? (2409)
- Do we write 249 or 2409? (2409)
- Does it make a difference? Why? (If the zero is not inserted to indicate zero tens, the 2 and 4 would be in the wrong place and it would look like there are 4 tens and 2 hundreds, a totally different number.)
- What does the zero tell you? (That there are zero tens)
- Use your pieces to partition 2409 in two more ways and record your work.
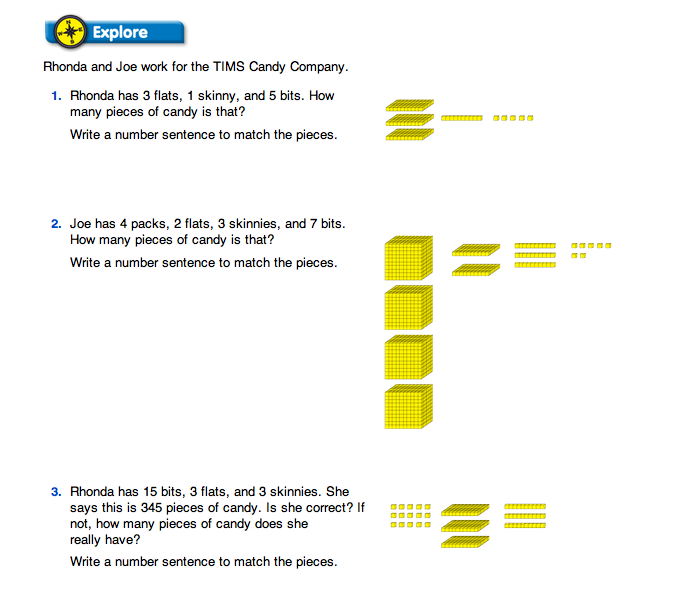
Have students answer Questions 1–8 on The TIMS Candy Company pages in the Student Guide.
Make sure they have the base-ten pieces available. As students are working, circulate and observe their work. Ask individual students to describe their strategies for solving the problems.
These questions may also be assigned for homework.