Addition

Est. Class Sessions: 2–3

Developing the Lesson

Part 2. Adding with Base-Ten Pieces and Paper-and-Pencil Methods

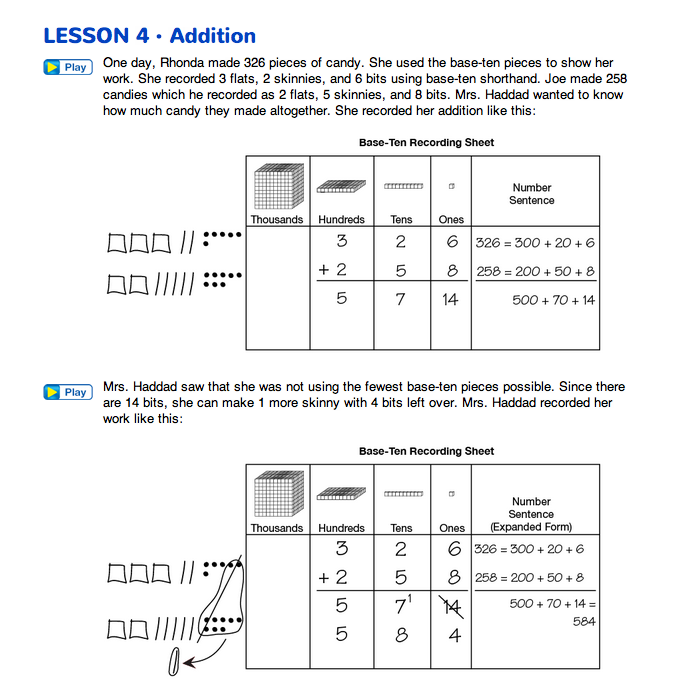
Show Problems and Compare Representations. In the following activity, students model addition problems using base-ten pieces and the Base-Ten Recording Sheet. Even students who are proficient with an algorithm can benefit from having the concepts of regrouping in addition reinforced with the base-ten pieces.

Display and pose the following problem:

Rhonda and Joe both work for the TIMS Candy Company. In two hours, Rhonda made 47 pieces of candy and Joe made 35 pieces of candy. How many pieces of candy did they make altogether?

Give 4 copies of the Base-Ten Recording Sheet Master to each student and ask student pairs to work together to show how to solve this problem using base-ten pieces or shorthand. Use Figure 3 to help students get started and to provide assistance with the recording where needed. Give students a few minutes to find a solution to the problem using whatever strategy they choose.

Ask a pair to share their solution strategy using a display of the Base-Ten Recording Sheet Master. Students should show the numbers using both base-ten shorthand and a number sentence. Once the numbers are recorded, students should show the class how they recorded and found the sum. See Figure 4 for one possible strategy.

For students who are having trouble with the recording sheet or partitioning numbers, discuss the information on the Base-Ten Recording Sheet. Ask them to compare the base-ten shorthand with the use of the numbers in the tens and ones columns, and with the solution using the expanded form. Have them identify what is the same and what is different and how the same action is reflected in the different methods and strategies.

How is the first number, 47, shown in all three representations? (In the base-ten pieces, it is 4 skinnies and 7 bits; in the tens and ones columns, it is 4 in the tens column and 7 in the ones column; in the number sentence column, it says that 47 is the same as 40 plus 7.)
How are those different representations alike? How do they relate to each other? (The 4 skinnies is 4 tens because each skinny is a ten; 4 tens is 40. The 7 bits is 7 ones because each bit is a one; the expanded form shows that in 47 there are 4 tens and 7 ones.)
What about when we got our answer? We showed our answer 3 different ways; how do those different ways relate to each other? (In the base-ten pieces after we made the trades, the answer is 8 skinnies and 2 bits; the skinnies are 80 and the bits are 2. That's 82. That's what we got adding the numbers after we made the trades.)

Ask students to compare the totals in the tens and ones columns with the totals in the number sentence column.

Ask:

How do they compare? What is the same and what is different? (Both are adding the tens and ones separately. In the tens column, the 7 means 7 tens, or 70; in the number sentence, it is written as 70.)
How do I write the final answer? Using the columns, it looks like the answer to this problem is either 712 or 7012. Are these answers reasonable? (Neither is reasonable.)
How do you know? (Possible response: I am adding two numbers that are both less than 50 so I know my answer has to be less than 100.)

Ask a student to show how to use the base-ten pieces to solve the problem.

How many bits are there when you add? (12 bits)
How many skinnies? (7 skinnies)
What is the total? (82)
How did you get that? (Possible responses: I had more than 10 bits after I added, so I traded 10 bits for another skinny; then I had 2 bits and 8 skinnies, 82.)
How can you show the trades on the Base-Ten Recording Sheet?

Figure 5 shows one way of recording the trades using base-ten shorthand and the recording sheet. Other methods are possible. Ask a student to record his or her trades and show them to the class.

Ask the class to consider the trades using prompts similar to the following:

What did [student's name] do when he or she added 7 bits and 5 bits and got 12 bits? (Traded 10 bits for a skinny or trade 10 ones for 1 ten.)
There are 12 ones in the ones column. How can you show when you are writing the numbers that you want to trade 10 ones for a ten? (See Figure 5.)

In this lesson, the bit is designated as one unit. To bridge the base-ten pieces and the base-ten system, gradually begin referring to the bits as ones, the skinnies as tens, the flats as hundreds, and packs as thousands.

Emphasize that the notation for showing the trade with the base-ten shorthand and the notation for showing the trade with the numbers both refer to the exact same action, i.e., trading the 10 bits for one skinny and trading 10 ones for one ten.

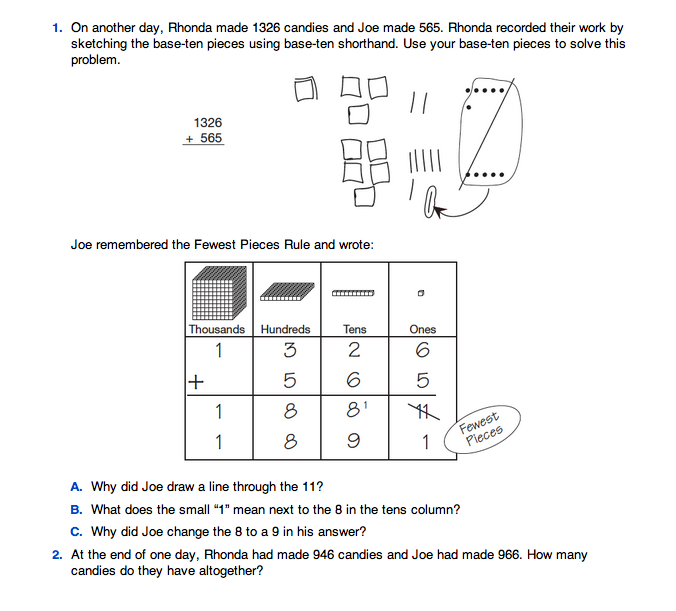
Ask pairs to use a Base-Ten Recording Sheet to solve the following problem:

Rhonda made 326 pieces of candy. Joe made 258 pieces of candy. How many pieces of candy did they make altogether?

Give students a few minutes to work on a solution and then ask them to open their Student Guides to the Addition pages. Ask students to compare their solutions with Rhonda's solution and Mrs. Haddad's work.

Ask:

What did Mrs. Haddad do differently from Rhonda? (She recorded her trades and then her total.)
How do the base-ten pieces relate to the number sentences? (The number sentence shows the total number of bits in each place and how they are organized into flats, skinnies, and bits.)

Ask students to work with a partner and read and complete Question 1 of the Addition pages. This question asks students to solve another problem using base-ten pieces and reminds students of the Fewest Pieces Rule. In the class discussion of Questions 1A–1C, be sure students connect the trades represented in the base-ten shorthand to the trades shown by Joe in the recording sheet.

Ask:

Why did Rhonda cross out the bits and draw a skinny? (She was trading 10 bits for one skinny to use the fewest number of pieces.)
Why did Joe draw a line through the 11? (He was also trading ten bits for a skinny to use the fewest pieces.)
What does the small “1” mean next to the 8 in the tens column? (He carried one skinny to the skinny column and then added them.)
Why did Joe change the 8 to a nine in his answer? (He had 9 skinnies once he traded the ten bits for one skinny.)
How did Joe end up with “1” in the ones column? (There was one bit left over after he traded ten bits for one skinny.)
Look back at the solution Rhonda started using the base-ten shorthand, and help her finish her solution. (Possible response: I added up the number of packs, flats, skinnies and bits: 1 pack, 8 flats, 9 skinnies, and 1 bit is 1000 + 800 + 90 + 1 = 1891.)

Have students solve another problem by asking them to solve Question 2 using any strategy they choose.

Use Paper-and-Pencil Methods. Once students have had a chance to solve the problem ask them to look at Rhonda's strategy, expanded form, in Question 3 and to answer Questions 3A–3D. These questions ask students to look at her strategy closely and explain what each part of her solution represents in the problem. Base-ten pieces or shorthand might help some students visualize what is happening in the expanded form method.

Ask:

Is this expanded form method similar to one of the strategies we have already posted?
If this strategy is not similar, should we add it to our collection of strategies?

Ask students to try this expanded form method by solving the addition problems in Question 4.

For example:

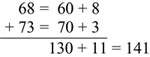
Choose a student to record his or her solution to one of the problems in Question 4 on chart paper so the expanded form can be added to the class collection of addition strategies.

Referring to Question 5, tell students that Joe decided to solve 946 + 966 using the all-partials method. Ask students to use Questions 5A and 5B to analyze Joe's solution. Once these questions are reviewed and discussed, ask students to try the all-partials method when they solve the addition problems in Question 6.

Ask:

Is this all-partials method similar to one of the strategies we have already posted?
If this strategy is not similar, should we add it to our collection of strategies?

Choose a student to record his or her solution to one of the problems in Question 6 on chart paper so that the all-partials method can be added to the class collection of addition strategies.

Referring to Question 7, tell students that Mrs. Haddad solved 946 + 966 using yet another method, called the compact method. Ask students to use Questions 7A–7C to analyze Mrs. Haddad's solution. Once these questions are reviewed and discussed, ask students to try the compact method when they solve the addition problems in Question 8. Record the solution for one of the problems in Question 8 on the chart paper so it can be added to the class collection of addition strategies.