Number Sentences

Est. Class Sessions: 2–3

Developing the Lesson

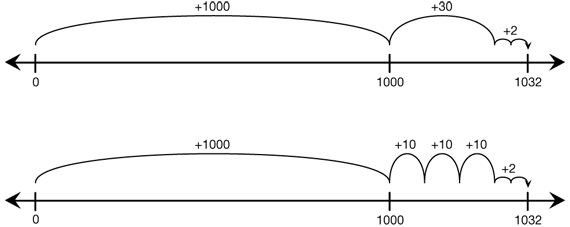
Examine Number Sentences and Equations. Refer to the opening vignette in the Student Guide and sketch the number lines. See Figure 1.

Ask:

How are the two number lines alike? (They both show moves from 0 to 1032. They both start with hops of 1000 and end with hops of 2.)
How are they different? (One shows 30 as one hop of 30 and the other shows 30 as 3 hops of 10.)
How do the number lines show the amounts on both sides of the equal sign are equal to 1032? Match each move with numbers in the number sentence. (1000 + 30 + 2 = 1000 + 10 + 10 + 10 + 2)

Discuss the term equation with the students using the vignette in the Student Guide. Ask whether it reminds them of any other word they have seen. Students should notice that the first part looks like the word equal. Tell them it is a word mathematicians use to describe a number sentence when the amounts on both sides of the equal sign are equal to each other.

Ask:

Are the amounts on both sides of Tanya's number sentence equal to each other? How do you know? (Yes ; 1000 + 30 + 2 = 1032)
Is Tanya's number sentence a correct equation? (Yes)

Ask students to work in pairs to complete Questions 1–7. As students work, ask them to tell you how they know their answers are correct. Use Tanya's discussion in the Student Guide as a model.

Students may complain of tedium in drawing and labeling each move, such as the multiple hops of 10 as in Question 3. If so, tell them the thirteen hops of ten can be written as one hop of 130, because 130 is a multiple of 10.

Replace Unknowns in Number Sentences. Have students read the vignette in the Unknowns section in the Student Guide. The vignette and Questions 8–10 introduce the idea of finding the value of an unknown in an equation. While this is clearly an introduction to an aspect of algebraic reasoning, students should solve the problems using their knowledge of place value and methods partitioning numbers rather than following a set of formal steps.

One method for completing the number sentences is to draw number lines to show that the values on both sides of the equation are the same. See Figure 2.

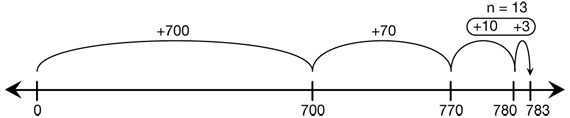
Have students work in pairs to complete Questions 8–10. One way to solve the problems is to use a counting-up strategy and a number line as shown in Ming's solution to Question 10 in the Student Guide and in Figure 3. Students can complete the problems and then compare solutions with partners.

If students have trouble getting started with the problems in Questions 8–10, ask them to draw number lines to show the moves on the side of the number sentence that does not have an unknown. Then have them draw a number line with the moves that are shown on the other side of the equation and reason to find the missing hop.

After reviewing Questions 8–10, assign Check-In: Questions 11–14.

Use Check-In: Questions 11–14 in the Student Guide and the corresponding Feedback Box in the Teacher Guide to assess students' abilities to represent and solve addition and subtraction problems using number lines [E2, E3] and to show that different partitions of the same number are equal to [E1].

Provide feedback to help students choose targeted practice on the Number Lines and Number Sentences pages in the Student Activity Book.