Lesson 4

Addition

Est. Class Sessions: 2–3

Developing the Lesson

Part 3. Choosing Appropriate Strategies

When appropriate, point out that a paper-and-pencil method is often not the quickest, nor most efficient way to solve the problem.

For example, ask:

X
  • Find different ways to add 2004 to 1876 without using one of the paper-and-pencil methods.

Discuss strategies with students and encourage them to find different ways of doing the problem. One person might add the 4 to 1876 to get 1880 and then add 2000 to get 3880. Another person might add the 2000 first.

Ask:

X
  • Is the strategy you used one that uses paper-and-pencil? Or is it one where most of the work can be done in your head?
  • What do you “see” in your head?
  • Does the strategy you used relate to the base-ten pieces? How?

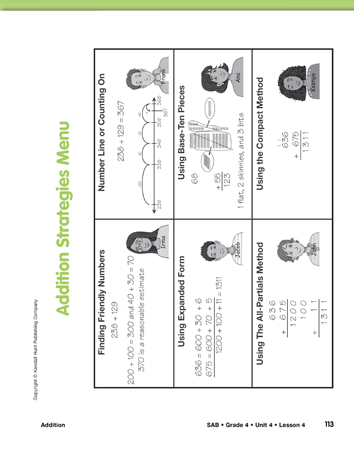
Refer students to the Addition Strategies Menu in the Student Activity Book. Ask students to compare the strategies on the menu to the strategies collected, discussed and posted. Check to see if the strategy they just used is on the menu.

Ask:

X
  • Is the strategy you just used similar to one represented on this menu?
  • Are there any other strategies that are not shown on the Addition Strategies Menu?
  • Which ones?
  • Do you think we should add this strategy to the menu?
  • Is this new strategy a mental math strategy or a paper-and-pencil strategy?

The Addition Strategies Menu in the Student Activity Book is blank on the back. Students can use the blank side to add their own invented strategy or reference another strategy. Identify a mental math strategy with a cloud or a thought bubble.

Now that students have several addition methods in their collection and the Addition Strategies Menu to summarize those strategies, students should explore which strategies work best in different situations. Ask students to solve the problem in Question 9 using any method they choose. Question 9B describes how Maya started a paper-and-pencil method and how John used a mental math strategy. Students are asked to complete each person's strategy and then choose the strategy they liked best for that problem.

Assign Questions 10 and 11 to give students more experience in choosing from a variety of strategies. Question 11 asks students to choose one problem to solve using a mental math strategy. The problems in Question 10A and 10B are good candidates for a mental math strategy. Encourage students to start asking themselves when a mental strategy seems to be the best strategy.

Question 12 asks students to look at mental math strategies and solve problems using those strategies. Questions 13 and 14 ask students to compare paper-and-pencil solutions to a problem and choose their preferred strategy for that problem.

X

When working with base-ten pieces at this point, some students may start with the tens, since they read from left to right. Students can work in either direction when using base-ten pieces, the all-partials method, or the expanded form method. However, when using the compact method (standard algorithm), it will be helpful for students to start with the ones digits. It is important to allow students to work with the pieces in ways that make sense to them. See the Mathematics in this Unit section for a summary of the methods presented in this unit.

As they build experience and confidence with the strategies, students will be better able to select more appropriate and efficient strategies. For now, getting students to explore the question of which strategy makes the most sense for a given problem is appropriate. They may not always agree on what is the most appropriate or efficient strategy. For some students the compact method may be one where error is common. Therefore, though efficient, it is not the best choice, because students are not confident with that strategy.

Student Guide: 132
Answers
X
SG_Mini
+
Student Activity Book: 113
X
SAB_Mini
+
Master: