Computation Methods

The development of computation methods in Math Trailblazers is based on the research of others in the field of mathematics education and our research in Math Trailblazers classrooms. Research by others corroborates the relationship between conceptual understanding and procedural fluency (Fuson & Burghardt, 2003; Fuson, 2003; Verschaffel, et al., 2007; National Research Council, 2001; NCTM, 2000; Hiebert & Wearne, 1996). For this reason, students using Math Trailblazers first develop their own methods for each operation. With these opportunities, students make connections between their understanding of place value and procedures for computation. As stated in Adding It Up: Helping Children Learn Mathematics, “Opportunities to construct their own procedures provide students with opportunities to make connections between the strands of proficiency. Procedural fluency is built directly on their understanding. The invention itself is a kind of problem solving, and they must use reasoning to justify their invented procedure. Students who have invented their own correct procedures also approach mathematics with confidence rather than fear and hesitation” (Kamii and Dominick, 1998 and National Research Council, 2001, p. 197).

Conceptual understanding supports procedural fluency with standard procedures and algorithms as well. Therefore, students learn to represent operations with base-ten pieces, number lines, or pictorial models. For the representations to be effective, students need sufficient opportunities and time to make connections between the models and numerical procedures. In summarizing findings of several researchers, the National Research Council reported, “Research indicates that students' experiences using physical models to represent hundreds, tens, and ones can be effective if the materials help them think about how to combine quantities and, eventually, how these processes connect with written procedures. The models, however, are not automatically meaningful for students; the meaning must be constructed as they work with the materials. Given time to develop meaning for a model and connect it with the written procedure, students have shown high levels of performance using the written procedure and the ability to give good explanations for how they got their answers” (National Research Council, 2001).

Throughout the unit, students share their own strategies with their classmates and read about possible strategies in the Student Guide. Comparing the various strategies and trying them out allows students to analyze the efficiency and usefulness of the methods in different situations (NCTM, 2000, p. 153).

Choosing Appropriate Strategies

Research in Math Trailblazers classrooms using previous editions indicates that students need support developing and using multiple computation strategies, instead of relying heavily on one procedure. Therefore, we have developed Strategy Menus for each operation to help students select appropriate methods for solving problems based on the context of the problem or the numbers involved. See Figure 1 for a menu of subtraction strategies from Lesson 5. The class develops similar menus for addition and multiplication in Lessons 4 and 10.

The menus remind students of strategies and methods they have practiced in class and help them choose appropriate methods for calculating based on the numbers in the problems. For example, students will arrive at accurate solutions more often if they have the flexibility to solve the subtraction problem 3001 − 2899 using a counting-up strategy, than if they use the traditional algorithm to subtract across zeros. See Figure 2. On the other hand, it is more appropriate to use the algorithm to solve 9524 − 3679.

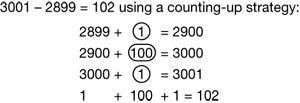
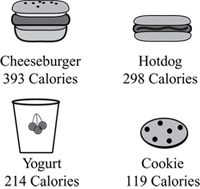
Students also use the menus to check their work for accuracy by choosing a second method to solve a problem and comparing the two answers. To solve the problem in Figure 3 efficiently, students need to develop the ability to identify it as an estimation problem and then solve it mentally using convenient numbers.

Partitioning Numbers

The ability to decompose and recompose numbers helps students understand more deeply the meaning of the computational algorithms they use and provides a greater flexibility in using them. The partitioning of numbers by place value (e.g., 1234 = 1000 + 200 + 30 + 4) is especially important when computing with larger numbers, both when using an algorithm and when using mental math.

For example, when using the traditional algorithm to solve the subtraction problem 1234 − 173, a trade is required. When the trade is made correctly, the minuend (top number) does not change in value. Rather, a different partition of the number is used to make subtraction possible.

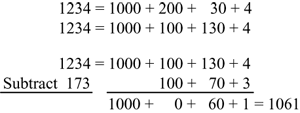
Without this understanding, a student who does not realize that the trade does not (and cannot) change the value of the top number (minuend) may make random changes to the top number in order to make it easy to subtract.

Using the Number Line

In this unit, students explore partitioning using base-ten pieces, number sentences, and the number line. Students using the number line develop images of the partitions that will help them solve problems using mental math.

Figure 4 shows two different ways that 6098 can be partitioned using a number line. As students find different ways to “get to” a number on the number line, they are also finding multiple ways to partition that number.

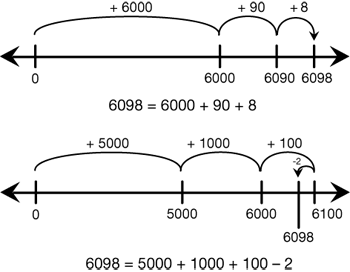
Each way can also be written using a number sentence. Students see how these equivalent expressions form number sentences, or equations:

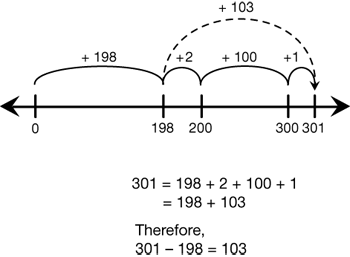
At the same time, students develop flexibility with all computations when they are not limited to partitioning by place value only. They should recognize, for example, that 301 − 198 can be solved by counting up from 198 to 301 and adding the partitions as shown in Figure 5. This method leads to efficient counting-up strategies for subtraction.

When unknowns are introduced into partitions as shown in the number sentence below, students are able to explore algebraic concepts as well.

An understanding of how numbers can be partitioned allows students to think of an unknown first as a “missing part,” rather than as a number to find via the formal rules of isolating variables.

Mental Math Strategies

Development of mental math strategies is an important outcome of students' study of whole numbers for two reasons. First, use of these strategies helps students in classrooms develop number sense and flexibility with numbers. Secondly, using mental math in the real world is often the most efficient means of solving problems, either for finding exact answers or for finding estimates when appropriate. Therefore, students need to have many opportunities to choose an efficient strategy for a given problem based on the numbers in the problem and the real-world context. For example, using mental math strategies to find exact answers to the subtraction problems in Figures 2 and 5 is more efficient than subtracting across zeros using the traditional algorithm. Similarly, using a mental math strategy to estimate is most appropriate for solving the problem in Figure 3 or to check exact answers for reasonableness.

Students should have opportunities to develop strategies that make sense to them. Some strategies may include some mental calculations along with a few written notes. For example, to solve 301 − 198 in Figure 5, students may visualize the number line but keep track of the hops by writing down the numbers: 2 + 100 + 1 = 103.

Discussing their strategies and explaining them in writing will help students clarify their own thinking and provide new ideas for others. However, it is important that students have opportunities to practice strategies that emphasize their efficiency. That is, when they choose to solve a problem mentally, they should not have to explain their thinking every time. For these reasons, students will see different types of directions for solving mental math problems in the unit. In some cases they are asked to explain their thinking in writing. At other times they are asked to share their thinking with a partner in discussion or to choose one problem out of a set of problems to show their reasoning in writing.

Practice is an essential part of mathematics. Fluency with basic procedures enhances conceptual understanding of new material. It is achieved gradually over time and is maintained with regular and consistent practice. In Math Trailblazers, computational practice is implemented according to the following considerations:

1. Practice is distributed over the curriculum. Students do short sets of problems frequently, rather than many problems all at one time, especially in the Daily Practice and Problems and Home Practice.
2. Practice is embedded in problem solving in the lessons, activities, and games.
3. Students practice material already mastered while learning new content.

This program of practice allows teachers to monitor students' use of computation strategies as they are being developed. Teachers can quickly identify incorrect procedures and help students correct them before they become ingrained.

This unit continues the review and assessment of the multiplication facts to develop mental math strategies, gain proficiency, and to learn to apply multiplication strategies to larger numbers. Students will focus on the multiplication facts for the 2s, 3s, and 9s.

Resources

• Fuson, K.C. “Developing Mathematical Power in Whole Number Operations.” J. Kilpatrick, W.G. Martin, and D. Schifter, eds. A Research Companion to Principles and Standards for School Mathematics. National Council of Teachers of Mathematics. Reston, VA, 2003.
• Fuson, K.C. and B.H. Burghardt. “Multidigit Addition and Subtraction Methods Invented in Small Groups and Teacher Support of Problem Solving and Reflection.” A.J. Baroody and A. Dowker, eds. The Development of Arithmetic Concepts and Skills: Constructing Adaptive Expertise. Lawrence Erlbaum Associates, Mahwah, NJ, 2003.
• Hiebert, J., and D. Wearne. “Instruction, Understanding, and Skill in Multidigit Addition and Subtraction.” Cognition and Instruction, 14(3), pp. 251–283, 1996.
• Kamii, C. and A. Dominick, The harmful effects of algorithms in grades 1–4. In L.J. Morrow and M.J. Kenney (Eds.), The teaching and learning of algorithms in school mathematics (1998 Yearbook of the National Council of Teachers of Mathematics, pp. 130–140). Reston, VA, 1998.
• National Research Council. “Developing Proficiency with Whole Numbers.” In Adding It Up: Helping Children Learn Mathematics. J. Kilpatrick, J. Swafford, and B. Findell, eds. National Academies Press, Washington, DC, 2001.
• Principles and Standards for School Mathematics. The National Council of Teachers of Mathematics, Reston, VA, 2000.
• Verchaffel, L., B. Greer, and E. Decorte. “Whole Number Concepts and Operations.” F.K. Lester, Jr., ed. Second Handbook of Research on Mathematics Teaching and Learning. Information Age Publishing Inc., Charlotte, NC, 2007.