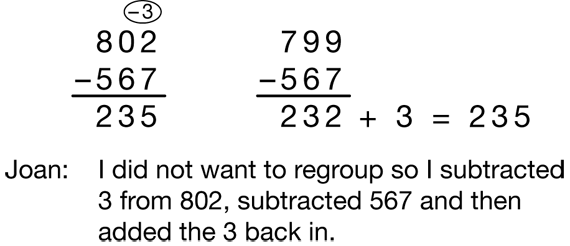Subtraction

The opening pages of the Subtraction pages in the Student Guide provide a written record of a problem solved with base-ten pieces and on a recording sheet, similar to the problems the students solved in Part 2. Ask students to read through the solution in the Student Guide and use their base-ten pieces to follow the steps in the first problem solved by Mrs. Haddad. Ask them to discuss Question 1 with a partner and then with the class.

Have students read through the next scenario. Students should talk with partners about the trades recorded in Joe's solution to 1237 − 459.

It is an important skill to be able to read and understand a solution in a math book. However, it is sometimes hard to understand someone else's marks when you do not know the order in which they were written. If students follow along with their own base-ten pieces as they read Joe's solution to the problem, they will be better able to understand the written solution.

Ask students to solve the problems in Questions 2–6. They can solve these problems on their own paper instead of on a recording sheet, using the traditional algorithm as Mrs. Haddad did. Use your judgment about whether some students would benefit from continuing to use the Base-Ten Recording Sheet to solve these problems.

If the strategy is not suggested by a student, show Joan's strategy in Figure 13 for Question 6H. Joan's strategy avoids regrouping.

After discussing the strategy, try a similar strategy for 702 − 346 and on the problem in Question 6D, 392 − 169.