Teacher Notes
X
TIMS Task
This item can be used as a Problem of the Week.
Students' strategies will vary. Allow students to develop their own solution paths. Some students will choose to solve the problem by calculating the total number of people in a stepwise fashion by adding the numbers together for each group that arrives. Other students may find a more efficient strategy by using a table as shown below and looking for patterns.
- Possible response: I started using a table like this one.
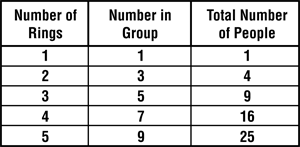
Then I noticed patterns. The numbers in the second column are the odd numbers. The numbers in the 3rd column are square numbers. I saw that the total number of people after 4 rings was 4 × 4 = 16 people and the total after 5 rings was 5 × 5, or 25 people. So I didn't have to write all the numbers in the table to find the total after 10 rings. It will be 10 × 10 = 100 people.
- The total number after 20 rings will be 20 × 20 or 400 people.
Challenge:
900 people after the 30th ring.
1600 people after the 40th ring.
P. Sally's Party



Sally is having a party. The first time the doorbell rings, one guest enters. Each time the doorbell rings after that, a group comes in that has two more people than the previous group had.
- How many people will have arrived after the tenth ring?
- After the twentieth ring?
Use a separate sheet of paper to show all your steps in solving the problem. Explain how you use any tools. Include strategies you tried that did not work or that you changed.
Challenge: How many people will have arrived after the thirtieth ring? After the fortieth ring?















