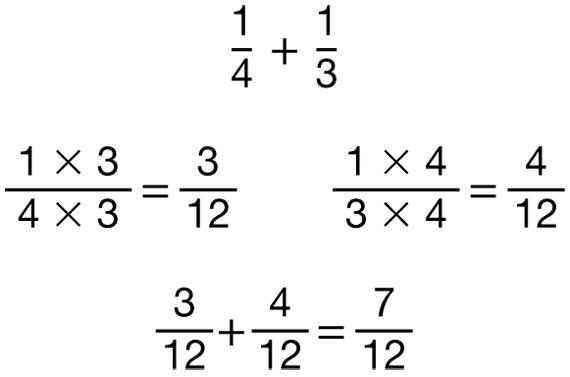Add Fractions

Use Circle Pieces to Add Fractions with Unlike Denominators. Read the opening vignette in the Add Fractions pages in the Student Guide. The discussion between Kathy and Romesh is a continuation of the vignette about the class pizza party from the previous lesson.

Assign Question 1. Students model the situation (1/2 + 3/8) using fraction circle pieces (Question 1A). Before solving to get an exact answer, Question 1B asks students to use their pieces to find out whether Kathy's estimate is accurate (i.e., whether the sum is less than one whole pizza). Then for Question 1C they use circle pieces to find an exact answer to the problem. They write a number sentence that corresponds to the solution in Question 1D.

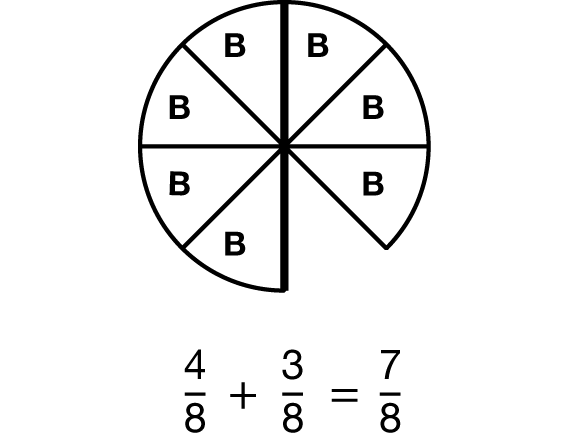
Ask students to read through Romesh's and Kathy's solutions. Romesh replaces one of the colors to get only pieces of a single color. He then adds the single-color pieces together as a fraction sum. Romesh's method, which we will call the “single-color method,” lays the foundation for finding common denominators to add fractions. See Figure 1 and the Content Note.

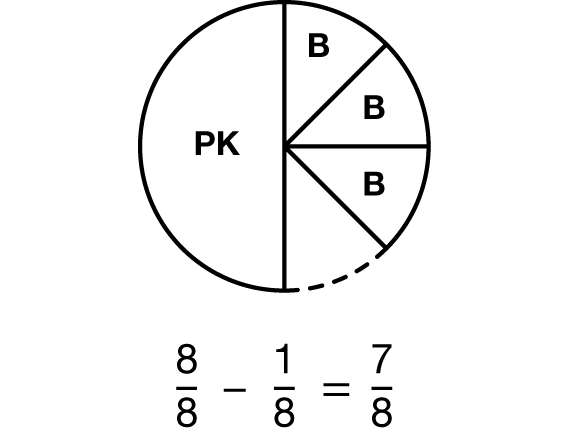
Kathy's method involves solving the problem by finding the missing piece from the unit whole (the red circle). She recognizes that the second addend, 3/8, is 1/8 less than one half, so the entire sum is exactly 1/8 less than one, or 7/8. See Figure 2.

Question 2 asks students to discuss similarities and differences among Romesh's, Kathy's, and their own solutions.

Use Circle Pieces to Add Fractions with Like Denominators. The problem in Question 1 requires finding the sum of fractions with two different denominators. When using the single-color method, one of the colors is replaced to match the second color. The problem in Question 3 involves adding fractions with like denominators. Therefore, no circle pieces need to be replaced before adding.

Have students read about Romesh's and Kathy's solutions and complete Question 4. Students compare Romesh's and Kathy's strategies for solving the cookie problem. Romesh's method again involves adding pieces of a single color. Kathy's method again involves finding the missing piece from the unit whole.

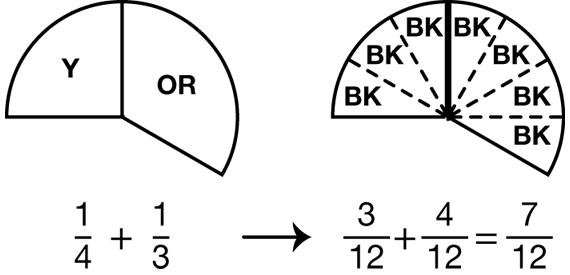
Question 5 involves addition of fractions with unlike denominators. After students complete the question using circle pieces, have them read Romesh's, Kathy's, and Julia's methods for solving the problem. Using Romesh's single-color method, both colors need to be replaced to achieve a single color. See Figure 3.

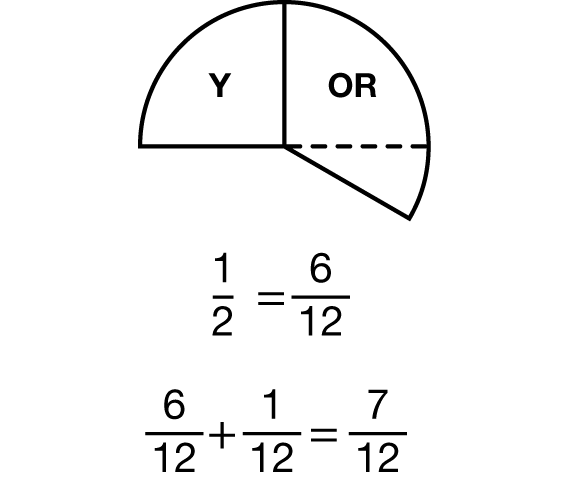
Kathy's method, however, does not use replacement. Rather, she compares the sum to the benchmark fraction of 1/2. She notices that the pieces extend beyond 1/2 by the equivalent of one black piece (1/12). Her method is like her strategies from the pizza and cookie problems, except that she finds the “extra” piece instead of the “missing” piece. See Figure 4.

Julia makes the connection between replacing the fraction circle pieces with all one color and using multiplication or division to find equivalent fractions with common denominators. See Figure 5.

Assign Question 6. Students are asked to note the variations and similarities in the ways that Questions 1, 3, and 5 can be solved.