Estimate Fraction Sums

Est. Class Sessions: 1–2

Developing the Lesson

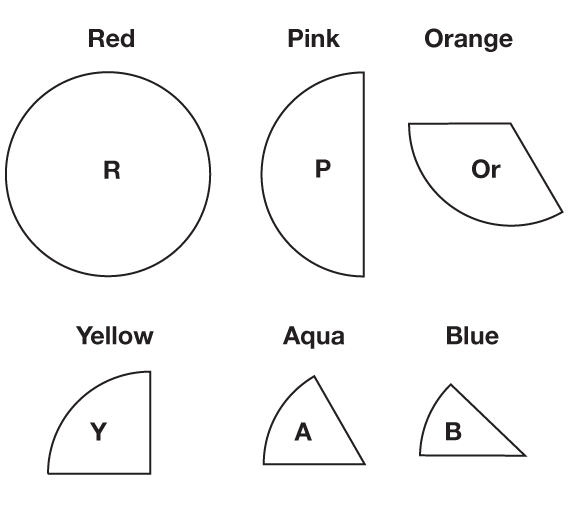
Estimate with Fraction Circle Pieces. Ask students to take out the red, pink, orange, yellow, aqua, and blue fraction circle pieces from their sets and to put the rest of the pieces away. See Figure 1.

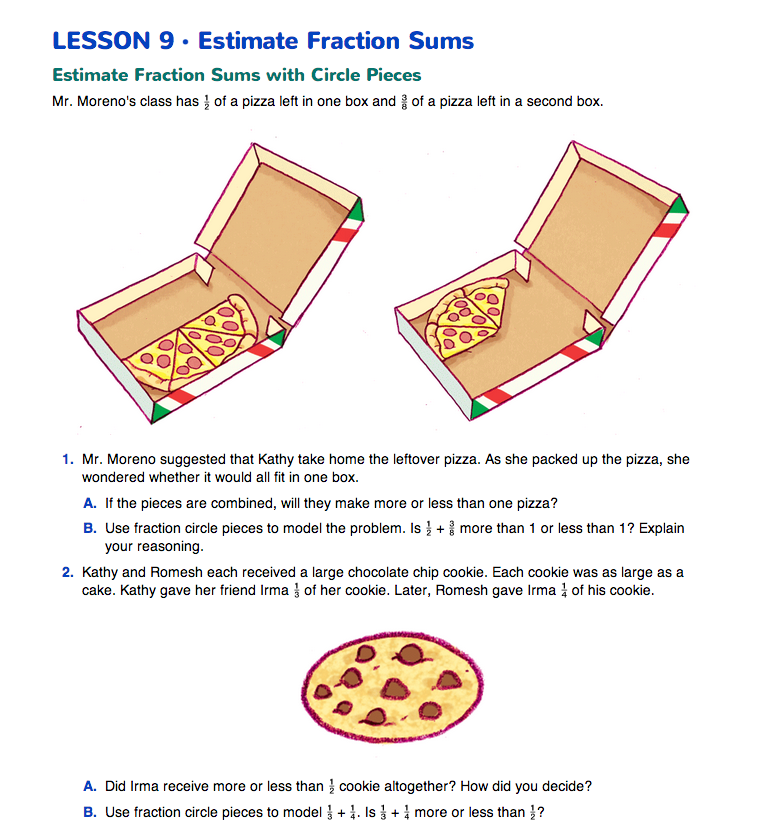
Direct students to the Estimate Fraction Sums pages in the Student Guide. These pages use a class pizza party as the context for estimating the sum of fractions. In Questions 1–4, students are asked to use the benchmarks 1 and 1/2 to help them make reasonable estimates of the sum of two fractions.

After reading the brief vignette that sets the context for the problems, ask students to work with a partner to solve Questions 1–2. Encourage students to use fraction circle pieces to model each problem. Be sure each student models each problem with his or her own pieces. Partners can then compare to see that they have the same answer. The time spent with the concrete models helps students develop mental images that will help them solve similar fraction problems when models are not available.

In Questions 3–4, students should first look at each problem and estimate if they think the fraction is more or less than the benchmark. They should then check the reasonableness of their estimate by using fraction circle pieces to model each problem.

Use Strategies to Estimate. In Questions 5–7, students solve problems without using fraction circle pieces. To introduce these problems, ask students to read how Kathy thought about whether she could combine the leftover pizza from two boxes into one box. Her reasoning showed that 1/2 + 3/8 is less than 1, so the pieces would fit in one box.

Ask students to solve Questions 5–7 and then share their thinking. In Question 5, they reason without using fraction circle pieces that 1/3 cookie plus 1/4 cookie is more than 1/2 cookie. Remind them that they solved this problem in Question 2 using fraction circle pieces.

Provide students many opportunities to talk about and share what they are doing as they solve the problems. They should talk with one another, with the class, and with you. This is a crucial part of the development of good communication skills. It will also help students formulate their written responses.

Students might describe their reasoning about the cookie problem by referring to the fraction circle pieces, even though this time they do not physically model the problem with the pieces:

1/3 of the cookie is like the orange piece. 1/4 is yellow. Two yellows make 1/2. An orange is bigger than a yellow. So an orange and a yellow make more than 1/2.

Other students might refer only to the fractions and not to the pieces:

She ate more than 1/2. 1/3 is bigger than 1/4. You only need 2/4 to make 1/2. So 1/3 plus 1/4 is more than 1/2.

After several student pairs have shared their thinking, ask:

How can you explain that 1/3 is larger than 1/4 without using fraction circle pieces? (Possible response: The smaller the denominator the larger the fraction, because it means the unit whole is divided into fewer pieces. If it is divided into fewer pieces, each piece will be larger. Since the numerator for both fractions is one, it means that we are talking about only one piece of each unit whole.)

Ask students to share their solutions for Questions 6–7.

Use these or similar prompts to guide them as they share:

What is one strategy you can use to decide if the sum of two fractions is less than or greater than one? (Possible response: Look at both fractions in the problem to see if they closer to one or to zero. If both fractions are close to one, the sum will be greater than one. If both fractions are closer to zero, then the sum will be less than one.)
Is there anyone who chose a problem to solve using that strategy? (Possible response for Question 3G: I looked at 7/8 + 2/3. Both 7/8 and 2/3 are close to one whole, so if you add them together the sum will be greater than 1. It will be close to 2.)
What strategy can you use if one fraction in the problem is close to one and the other is close to zero? (Possible response: You can think about the bigger fraction and think about how much of the whole would be left and then decide if the smaller fraction is larger or smaller than that space.)
Is there anyone who chose a problem to solve using this strategy? (Possible responses for Questions 3A and 3C: For Question 3A, I saw that 2/3 was close to one. There would be 1/3 of the whole left. I know that 1/8 is smaller than 1/3 because both have 1 as the numerator so the smaller the denominator the larger the fraction. That means that 2/3 + 1/8 will be a little less than 1 whole. For Question 3C, I know that 7/8 is almost 1 whole. There would be 1/8 of the whole left. I know that 1/4 is bigger than 1/8 because when you divide a whole into less pieces, each piece is bigger, so 7/8 + 1/4 is a little bigger than one.)
How can you use these or similar strategies to decide if the sum of two fractions is greater than 1/2 ? (Possible response: First I would look at both fractions. If one or both fractions are greater than 1/2, then the sum of the two fractions will be greater than 1/2. If both fractions are less than 1/2, then I need to see if each fraction is closer to 1/2 or to zero.)
Who will share a strategy they used to solve one of the problems in Question 4? (Possible response for Question 4B: 1/4 is equal to 2/8. 1/8 + 2/8 = 3/8. Since it takes 4/8 to equal 1/2, 3/8 is less than 1/2. Possible response for Question 4F: 1/3 + 1/3 = 2/3. I know that 1/2 = 2/4 and that 2/3 is larger than 2/4, so 2/3 is larger than 1/2.)

Continue asking questions and sharing strategies until a variety of students have had an opportunity to share.

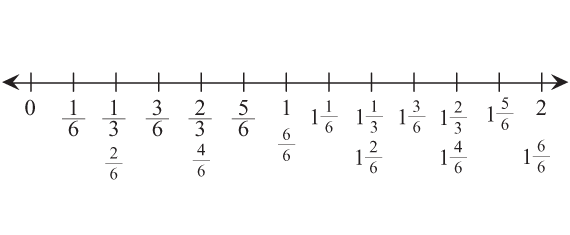
Use Number Lines to Estimate. Direct students to the Estimate Fraction Sums with Number Lines pages in their Student Activity Book. In Questions 1–5, students use number lines to visualize the relative size of fractions since the fractions are listed in order. Ask students to work with their partners to solve these questions. Encourage them to use the number lines as they work. Note that not all fractions in the problems are labeled on the lines. Students should reason about where the unlabeled fractions are located.

For example, as students are working on Question 2, ask:

I don't see 1/6 on either number line. Where would I put it if I labeled it on one of the number lines? (Possible response: I know 1/3 is equal to 2/6, so I would label it on the line that shows thirds. 1/6 would go halfway between zero and 1/3.)

If students have difficulty solving this problem using the number line, ask them to think about how they can divide the number line into sixths and label it from 0/6 to 12/6. See Figure 2.