Introduce Numerators and Denominators. Use the vignette on the Wholes and Parts pages in the Student Guide and the questions that follow to introduce this lesson. After reading the introduction, ask students to work with a partner to discuss Question 1.
Use these or similar discussion prompts to guide a discussion.
- When Irma said she ate 1/2 of a cake, what does the number 1/2 mean? (Possible response: It means that Irma took a whole cake and divided it into two equal pieces and then she ate one of the two pieces.)
- If all of the students heard Irma share the same information about eating 1/2 of a cake, why do you think each one had a different thought about what she ate? (Possible response: Irma did not tell them what the whole cake looked like so they each thought about a kind of cake they liked.)
- What information does Irma need to include that would help her friends understand how much cake she actually ate? (Possible response: She would have to tell them the size and shape of the whole cake.)
Continue the discussion about fractions by reading the Numerators and Denominators section in the Student Guide. Remind students that when Irma said she ate 1/2 of a cake, the denominator in the fraction (the two) means that her cake (the unit whole) was divided into two equal pieces and the numerator (the one) means she ate one of the two pieces. Have students work with their partner to read and discuss Questions 2–4.
In Question 4, students review the idea that equal fractional parts of a unit whole must be the same size. However, the parts need not be the same shape.
- What does it mean to divide a unit whole (the cake) into fourths? (The shape is divided into four equal parts.)
- How do you know that David's cake is not divided fairly into fourths? (There are four pieces but they are not all the same size.)
- How do you know Jerome's cake is divided fairly? (Possible response: First Jerome divided the cake into two equal pieces or halves. Then he divided each half into two equal pieces or halves again. He made one cut up and down and the other across, but he still divided each half into two equal pieces. That means he cut the cake into 4 equal size pieces, or fourths.)
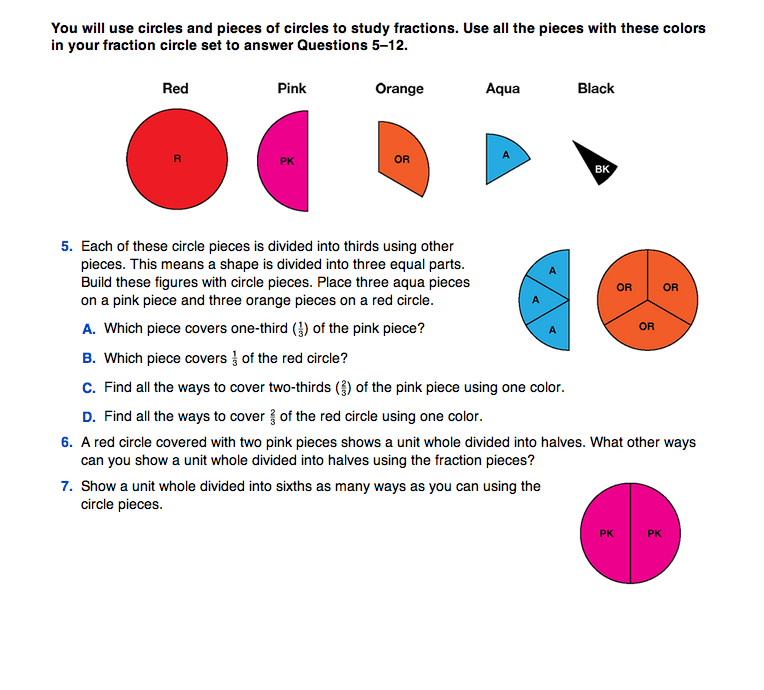
Write Fractions with Words and Numbers. Students will use the fraction circle pieces to help them think about fractions and the unit whole. Storing the individual sets in resealable plastic bags provides easy access to all pieces. Ask students to take out the red, pink, orange, aqua, and black circle pieces from their set and put the rest away. See Figure 1.
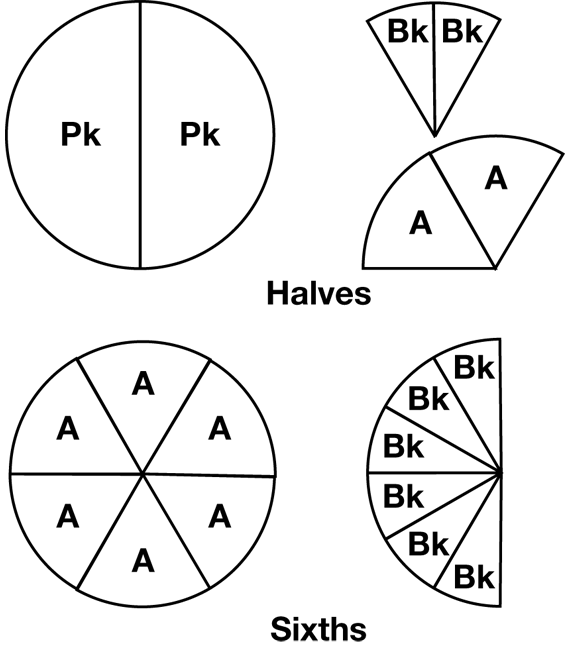
Ask students to work with their partners to complete Questions 5–7 using the fraction circle pieces. These questions continue the ideas introduced in Questions 1–4. For example, for Question 6, students must find all the ways to show a unit whole divided into halves, and for Question 7 they must show sixths. To answer these questions, they must understand that any of the pieces can represent the unit whole and that the whole must be divided into equal size parts. Figure 2 shows solutions to Questions 6–7.

Students used fraction circles to explore fractions in earlier grades. If you have students who are new to Math Trailblazers or who need additional practice with fraction circles, they can complete the Use Fraction Circle Pieces Master in the Teacher Guide.
Some questions ask students to make drawings (e.g., Questions 3B and 4A) to help them develop visual images of the pieces. Other questions give students a choice between making a drawing and writing a response in words (e.g., Questions 5B, 6B, and 7). This allows students to choose the representation that makes sense to them. Drawings will be a natural way for some students to show solutions. Other students may prefer to describe their solutions in words.
Point out to students that when they make drawings, they need only make sketches so that someone else can understand what they did. They need not take a lot of time drawing the pieces exactly to scale. Students can also trace the pieces they use. Encourage students to label the pieces with the colors as shown in the Student Guide to show the pieces they use.
Use these or similar prompts and display sets of fraction circle pieces to guide a class discussion.
- If the pink piece is the unit whole, which pieces will you use to divide it into three equal parts? (three aqua pieces)
- What fraction does each piece represent? (one-third)
- If the red circle is the unit whole, which pieces will you use to show it divided into three equal parts? (three orange pieces)
- Which pieces can you use to represent two-thirds of the red circle? (two orange pieces)
- Which pieces can you cover with two pieces of the same color, dividing the piece in half? (You can cover the red with two pink pieces, the orange with two aqua pieces, and the aqua with two black pieces.)
- Which pieces can be divided into six equal parts? (The red circle can be covered with 6 aqua pieces and the pink half circle can be covered with 6 black pieces.)
Students continue their exploration of fractions as they work with their partners to complete Questions 8–18. These questions ask students to model various fractions and mixed numbers when given a whole, and give the whole when given a fraction. Encourage students to use the Writing Numbers in Words page in the Student Guide Reference section to help them write the fractions in words. Students use the red, pink, orange, aqua, and black pieces to answer Questions 8–12. Questions 13–18 direct students to use the red, pink, green, and purple circle pieces. Circulate throughout the classroom.
As you observe students working, use these or similar prompts to check student understanding:
- When you write a fraction, how do you decide what number to use in the denominator? Numerator? (Possible response: The denominator tells how many pieces the whole is divided into. The numerator tells how many pieces you are considering or talking about.)
- When you know the fraction represented by a piece, how can you use that to find the unit whole? (Possible response: If you know how many pieces the whole is divided into, you can put them together to find the shape of the unit whole.)
- How can you tell if two fractions are equal? (Possible response: If the two fractions cover the same area or space, they are equal.)
- What does it mean when you see the fraction 2/1? (The one in the denominator means that you are talking about the unit whole. The two in the numerator means you have 2 unit wholes, or 2.)
- What does it mean when you see the fraction 2/2? (When the numerator and denominator are the same it tells you that you have all the pieces into which the unit whole is divided, so you have one.)
- How can you write 4/3 as a mixed number? (11/3)
- How can you write 11/3 as an improper fraction? (4/3)
- How do you know that 2/10 is equal to 1/5? (Possible response: If you put 2/10 on top of the piece for 1/5 it will cover exactly the same area, so they are equal. Or, 1/10 covers half of 1/5 so 2/10 will cover the whole 1/5 piece.)
- How are decimals and fractions the same? (Possible response: They are both numbers and both ways to represent a whole divided into equal pieces.)