Use Circle Pieces to Define Equivalent Fractions. For this part of the lesson, students will continue to work only with the red, pink, yellow, blue, and black pieces.
Equivalent Fractions. In mathematics, two fractions that have the same value are considered equivalent fractions. At this level of mathematics, we do not distinguish between the words equal and equivalent. Therefore, it is acceptable for students to use either equal or equivalent when comparing two fractions that have the same value.
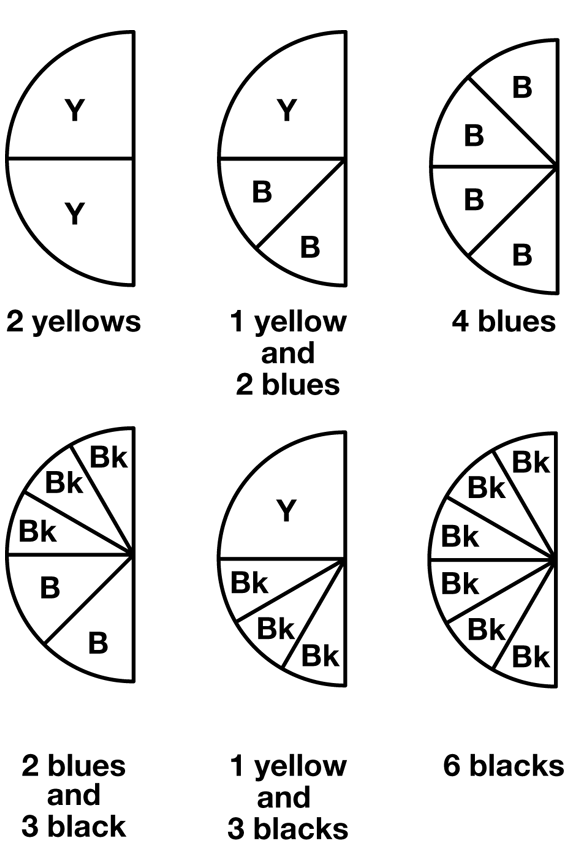
Begin by displaying a pink piece. Ask students to work with a partner to find as many ways as they can to cover the pink piece using a combination of the pieces. Possible responses are shown in Figure 3. As students report their solutions to the class, ask them to write the names of the pieces they used as shown in the figure.
- Which ways use only one color? (2 yellows, 4 blues, and 6 blacks)
- What fraction of the red circle is covered each time? (one-half of the red circle)
- If the red circle is the unit whole, what fraction can you write for two yellows? (2/4)
- What fraction can you write for the 4 blues? (4/8)
- What fraction can you write for 6 blacks? (6/12)
Tell students that fractions that have the same value are called equivalent fractions. Draw students' attention to the fact that one pink, two yellows, four blues, and six blacks all cover 1/2 of the red circle. So 1/2, 2/4, 4/8 and 6/12, are all equal to one another.
Use Circle Pieces to Find Equivalent Fractions. Tell students to add the orange and aqua circle pieces to those they already have on their desks. Students will use the red, pink, orange, yellow, aqua, blue, and black pieces for this part of the lesson.
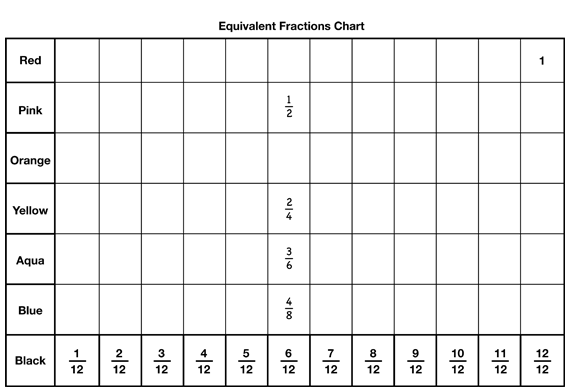
Show students the Equivalent Fractions Chart prepared before the lesson or a display of the Equivalent Fractions Chart page from the Student Activity Book. Write 1/2 on the chart in the appropriate box, as shown in Figure 4.
- Why did I write 12 in this column? (It is equivalent
to 6/12.)
- How did I know which row to put it in? (It's a pink piece so it goes in the pink row.)

Talk with students as they work on the puzzles. For students who are having trouble getting started on a given puzzle, provide clues on how to begin. Sample prompts follow for Puzzle 3:
- What piece would you start with? What piece covers the most of the red circle? (pink)
- How much of the circle is left to cover? (Another half. Another pink.)
- Do you know how many blues it would take to cover a pink piece?
- How many blues are the same as a yellow? (2 blues)
- How many blacks are the same as the yellow? (3 blacks)
For students who readily see the puzzle solution, ask questions that will enable them to articulate their thinking:
- I see that you saw the solution right away. How did you do that?
- What piece did you think of first? Why? (Possible response: I know that pink was half and it was the largest.)
- How did you know what to do with the other pieces? Did you divide up the other half of the circle in your head? How? (I thought back to the example. I knew that the other half is the same as two yellows or fourths. Then I tried to think of a way to use blues and blacks to cover the fourths.)
- Did you know that some pieces would not work? How did you know that? (Possible response: I knew I only needed two blues to cover a fourth, so I didn't need one of the blues.)
Ask volunteers to write 2/4 and 4/8 in the appropriate boxes so that all the fractions in that column are equivalent.
- Look at the pieces that are on your desk now. Can you use any other pieces to cover the pink piece and represent another fraction equivalent to 12 ? (3 aquas)
- What fraction of the circle piece does 3 aquas represent? (1/2 or 3/6)
- Where will 36 go on the Equivalent Fractions Chart? (In the row for aqua and the column for 6/12.)
- What boxes in the column for 612 do not have fractions yet? What rows are they in? (The rows for red and orange.)
- Why isn't the box in the row for red filled in? (The red circle is the whole. It is bigger than 1/2.)
- Can we fill in the box in the row for orange? Why or why not? (No. Possible response: One orange piece fits on a pink, but not two. Or, no number of orange pieces fit exactly on a pink piece.)
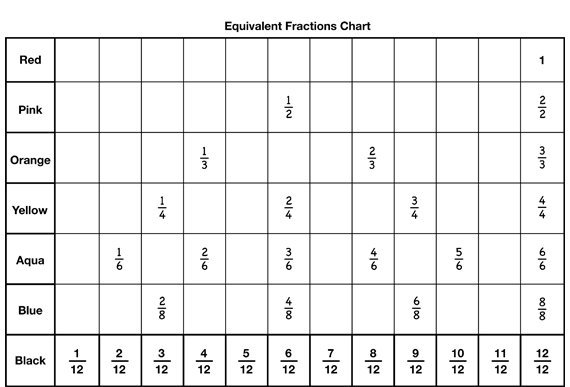
Ask students to find their Equivalent Fractions Chart in the Student Activity Book and fill in the column for 6/12. Then direct their attention to the column for 12/12 and ask them to fill in the chart with equivalent fractions. Ask volunteers to add fractions to the class chart and show the fraction with circle pieces (e.g., 4 yellows represents 4/4). Emphasize that fractions are equivalent if they cover the same amount of the circle. Each of the fractions in the last column is equal to one whole.
As students work, ask them to look carefully at the fractions in the two columns and discuss the following with their partners:
- What patterns do you see in the fractions that are equivalent to 1/2? (Possible responses: All the denominators are even numbers. The denominators are twice the numerators. The numerators are half the denominators.)
- Why do these patterns work? Think about what the numerators and denominators mean. (Possible response: All the fractions are 1/2 of the red circle. The denominator tells how many would cover the whole circle and covering 1/2 will take half the pieces.)
- What patterns do you see in the fractions that are equivalent to one whole? (Possible response: The numerators equal the denominators.)
- Why does this pattern work? (Possible response: The denominator tells how many pieces cover the whole and the numerator tells how many pieces cover the fraction we are talking about. To equal one whole, the whole circle must be covered with pieces. So the numerator will equal the denominator.)
When students have completed the columns for one half and one whole, ask them to work with their partners to make predictions.
- You are going to complete the chart by finding all the fractions in each column that are equivalent to the fractions in the bottom row. Look at the whole chart now. Predict what the chart will look like when all the equivalent fractions have been added.
- Will all the boxes be filled in?
- Will any of the columns above the twelfths row be empty? If so, which columns? Why? If not, why not?
- Will you be able to use any patterns to fill in the chart? If so, which patterns?
- Which row do you think will have the most fractions? Why?
Write down a few of the predictions. Then ask students to use their own strategies to find the equivalent fractions and complete the chart. Encourage them to help each other and to share their strategies. The completed chart is shown in Figure 5.

Some students may need some additional help to get started filling in the chart. Focus students on the next largest piece, the orange piece. Ask these students:
- What fraction of the red circle does the orange piece cover? (1/3)
- What is one way you can cover the orange piece with the same color pieces? (4 blacks or 2 aquas)
- What fraction of the whole does four blacks represent? What fraction does 2 aquas represent? (4/12, 2/6)
- What fractions are equal to 4/12? What fractions cover the same part of the red circle? (1/3 and 2/6)
- Where will you write them on the chart? In what rows? (in the column for 4/12 in the rows for orange and aqua)
For students who finish quickly, ask them to look for patterns in the chart and to find ways to explain why the patterns work. Then ask them to use the patterns to predict where the fractions for green and purple pieces will go on the chart and to check their predictions.
When students have completed their charts, ask them to look back at the charts and their predictions.
Use prompts similar to the following:
- Did you fill in all the boxes on your chart? Why or why not? (No; Possible response: We were not able to find any equivalent fractions using many of the fraction pieces.)
- What patterns do you see in the chart? (Possible responses: There are no equivalent fractions for 1/12, 5/12, 7/12, and 11/12. The aqua pieces were used the most for making equivalent fractions. You can use every piece to find equivalent fractions for 1. The fraction with the second highest number of equivalencies is 1/2.)
- What patterns do you see going across the rows? (Possible responses: The denominators in each row are the same, the numerators go up by one as you read across except in the blue row. That numerator starts with 2 and goes up by 2. In all the rows except the blue row, the denominators are factors of 12. The numerator and denominator for the last fraction in each row is the same. As you go across each row, there is an equal number of blank spaces between each fraction. For example, as you go across the yellow row there are two blank spaces between each fraction.)
- What patterns do you see going down the columns? (Possible responses: In the last column each fraction has the same numerator and denominator. I noticed that the shape made by the numbers in the chart is a triangle shape.)
- Were you able to use any of the patterns to help you complete the chart? If so, how? (Possible response: Yes, I used the pattern in the numerators and denominators going across each row.)
Ask volunteers to fill in the classroom display of the Equivalent Fractions Chart with all of the equivalent fractions they found.
Use Multiplication and Division Strategies to Find Equivalent Fractions. Direct students to the Find Equivalent Fractions pages in the Student Guide. In Questions 1–4 students will work with a partner to find equivalent fractions using multiplication and division strategies. As students are working, encourage them to refer back to either the completed display of the classroom Equivalent Fractions Chart or to their completed Equivalent Fractions Chart in the Student Activity Book. Students can also use fraction circle pieces, as needed.
To solve Question 1, students can use the multiplicative relationship between numerator and denominator in each fraction to help them decide if 10/30 is equivalent to 1/3. For each fraction: 1/3, 2/6, and 4/12 the denominator is 3 times the numerator. In the fraction 10/30, this relationship is also true: 10 × 3 = 30, so 10/30 = 1/3. Students may also see that for each fraction, if you divide the denominator by the numerator, the answer is three. Since 30 ÷ 10 = 3, they can see that 10/30 = 1/3. Students may also remember that you can find equivalent fractions by multiplying both the numerator and denominator by the same number. Since 1 × 10/3 × 10 = 10/30, you know that 1/3 = 10/30.
In Questions 2–3, students continue to explore using multiplicative strategies to find equivalent fractions.
- Why does multiplying both the numerator and denominator by the same number result in an equivalent fraction? (Possible response: When you multiply both the numerator and denominator by the same number it is like multiplying by one. That means the fraction has the same value, but it just divided into a different number of pieces.)
- What strategy can you use to decide if 2/6 = 7/21? (Possible responses: You can look at the relationship between the numerator and denominator in each fraction. If the relationship is the same then the two fractions are equivalent. For example, in the fraction 2/6, if you divide 6 by 2 the answer is 3. In the fraction 7/21, if you divide the 21 by 7 the answer is also 3. That means that 2/6 = 7/21. You can use fraction circles to see that 2/6 = 1/3. You can multiply both the numerator and denominator for 1/3 by 7, 1 × 7/3 × 7 = 7/21, so 1/3 = 2/6 = 7/21.)
- Does this strategy work when you are trying to decide if 4/6 = 9/15? (Possible responses: For these fractions you can't divide the denominator by the numerator because 4 is not a factor of 6 and 9 is not a factor of 15. You can use fraction circles to find that 4/6 = 2/3. You can then see if there is any number that you can multiply the numerator and denominator by to get 9/15. Since 2 can't be multiplied by any number to equal 9, you know that 2/3 is not equal to 9/15, so 4/6 is also not equal to 9/15.)
- How do these strategies help you decide if 3/12 = 5/20? (Possible responses: I know that if I multiply three times four the answer will be 12, and if I multiply five times four the answer will be 20. Since you can multiply the numerators in both fractions by four to equal the two denominators, these fractions are equivalent. You can use the Equivalent Fractions Chart to see that 3/12 is equal to 1/4. The fraction 5/20 is also equal to 1/4, because if you multiply both the numerator and denominator in 1/4 by 5 it will equal 5/20.)
In Question 4 a division strategy is used to explore equivalency.
After sharing their strategies for finding equivalent fractions in Questions 1–4, students can continue to work with a partner to complete Questions 5–8. As students are working, encourage them to share their strategies with one another. Circulate throughout the room and observe their ability to use multiplication and division strategies to find equivalent fractions.
Assign Check-In: Question 9 to students to complete independently. Students apply their knowledge of fractions in a problem-solving context. Before students begin, display and direct students to the Math Practices page in the Reference section of the Student Guide. Ask students to read Math Practice Expectation 2, Find a strategy, and 5, Show my work.
- What are the tools and strategies you have been using to find equivalent fractions? (Possible response: Tools you can use include the fraction circle pieces, the display of the Equivalent Fractions Chart, or drawings. You can also use strategies for multiplication and division.)
- In Question 9D you are asked to explain your thinking. What should you include to make sure others know what you were thinking? (Possible response: You need to make sure you answer the question that is being asked. You should use words or drawings to help others understand your answer.)
Use Check-In: Question 9 on the Find Equivalent Fractions page in the Student Guide and the corresponding Feedback Box in the Teacher Guide to assess students' abilities to find equivalent fractions using area models and multiplication and division strategies [E4].
Question 9D can also be used to assess students' abilities to find a strategy [MPE2] and show work [MPE5].