Display the following equation:
- Is the sum closer to 0, 1/2, or 1? How do you know? (Possible response: 3/8 is close to 1/2 so 1/2 + 3/8 will be close to 1. Adding 1/4 will make it more than one.)
Ask students to model this problem with a partner using circle pieces.
After a minute or two, ask:
- How is this problem different from others you have solved so far? (Possible response: The pieces fill more than one full circle.)
- Use the display set of fraction circle pieces to show your model. Why did you group your pieces that way?
- How did you solve the problem, and what answer did you get? (Possible response: I used the single-color method, like Romesh. I replaced all the pieces with blue pieces. I counted the 9 blue pieces and got 9/8.)
- Did anyone solve the problem a different way? (I filled one full circle with the pink piece, the yellow piece, and two blue pieces. I had one blue piece left over. Since 8 blue pieces cover one whole, each blue piece is 1/8. Since I had one whole and 1/8, my answer was 11/8.)
- Show how to use common denominators like Julia did and see if you get the same answer. (1/4 × 2/2 = 2/8; 1/2 = 4/8; 2/8 + 4/8 + 3/8 = 9/8)
- Is this a true number sentence: 11/8 = 9/8? How do you know? (Possible response: Yes, 11/8 is equivalent to 9/8. I know 8/8 make a whole or 1, and then there is 1/8 extra.)
- Did you estimate the sum to be closest to 0, 1/2, or 1? Was your estimate correct?
Read the vignette in the Fraction Sums Greater Than One section in the Student Guide. Assign Questions 11–12. Students are asked to solve a problem using a method different from Romesh's way and to practice finding common denominators like Julia.
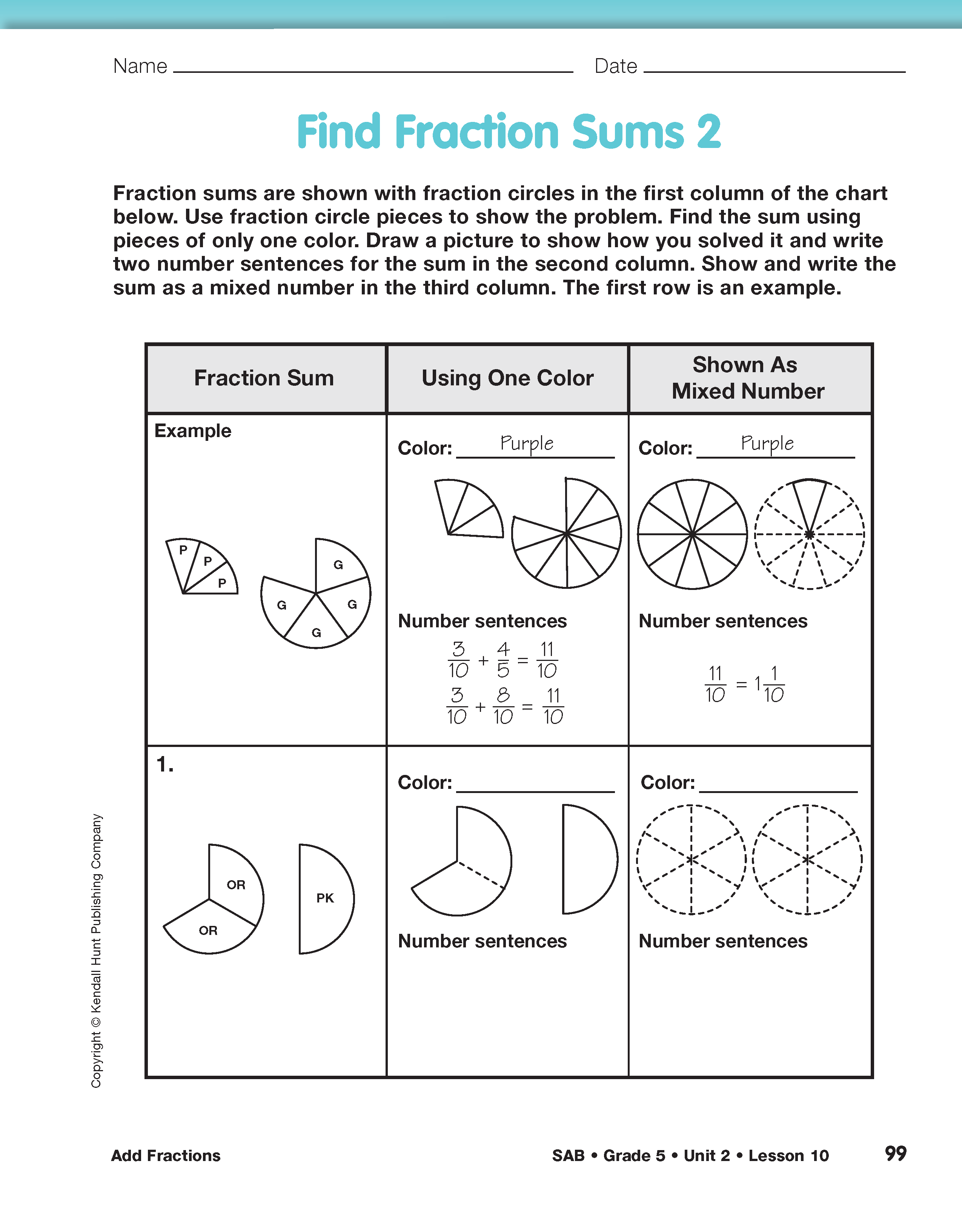
To provide further practice finding sums greater than one using circle pieces and common denominators, display and direct students to the Find Fraction Sums 2 pages in the Student Activity Book. Demonstrate the example problem 3/10 + 4/5 using display fraction circle pieces.
- How is replacing the circle pieces with all purple pieces like finding equivalent fractions with common denominators? (We replace the green circle pieces with all purple pieces because then we can just count the number of purple pieces, tenths in this case, to find 11/10. We can find equivalent fractions with the common denominator 10 to add like fractions.)
- How do the number sentences match with the model? (3 purples show 3/10 + 4 greens show 8/10, which equals 11 purples or 11/10. Replacing the green pieces with all purple is like 3/10 + 8/10 = 11/10.)
- How do you know 11/10 is equivalent to 11/10? (Possible response: 10/10 = 1, and the eleventh tenth makes 11/10.)
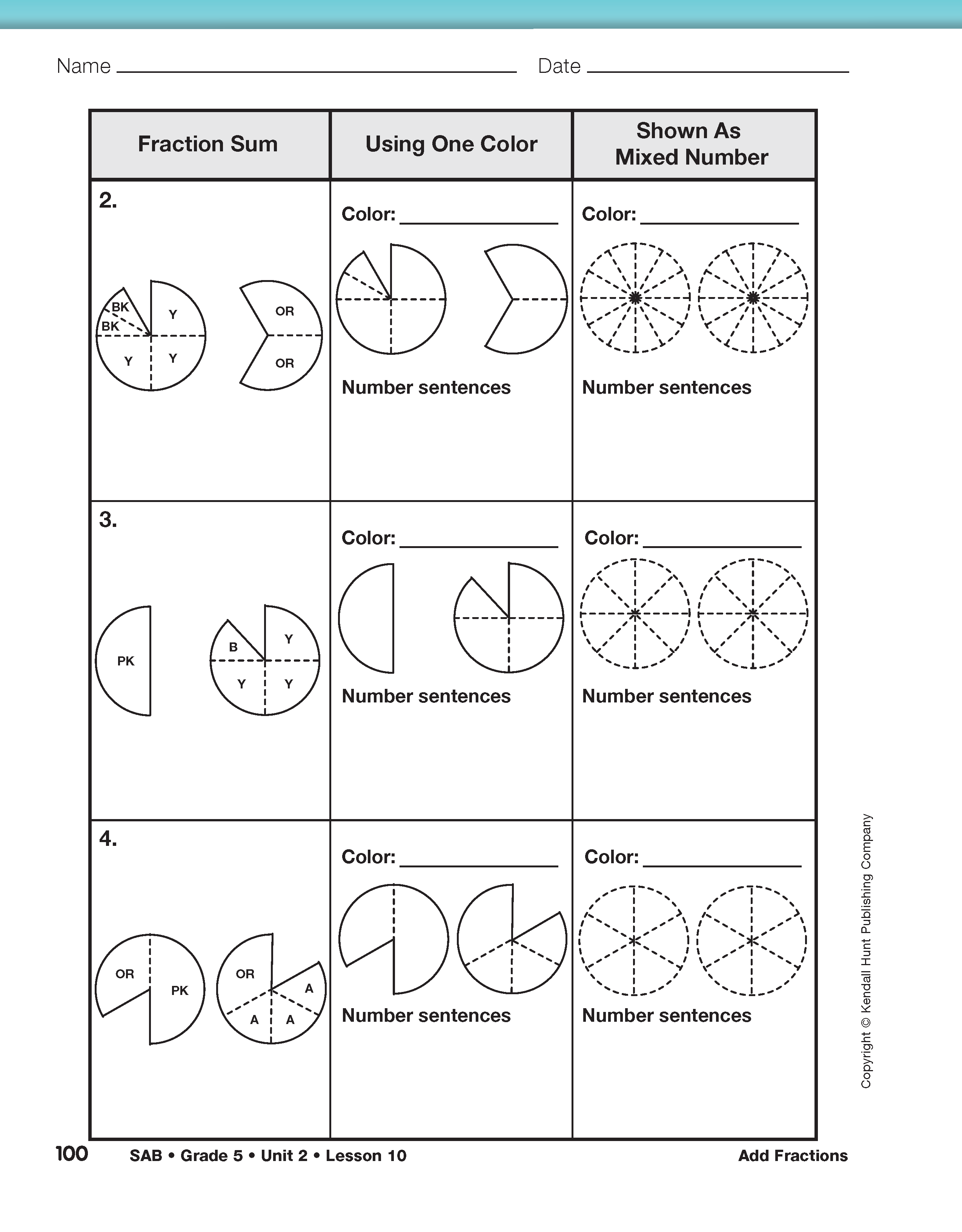
Assign Questions 1–6 to student pairs. Upon completion, ask several students to share their solutions to Question 6A–C with the class. Ask one student or student pair to show how to model the problem using display circle pieces. Ask a second student or student pair to show how to solve the problem by finding equivalent fractions with common denominators.