Compare Fractions to Benchmarks

Est. Class Sessions: 2–3

Developing the Lesson

Part 1. Use Benchmarks to Compare Fractions

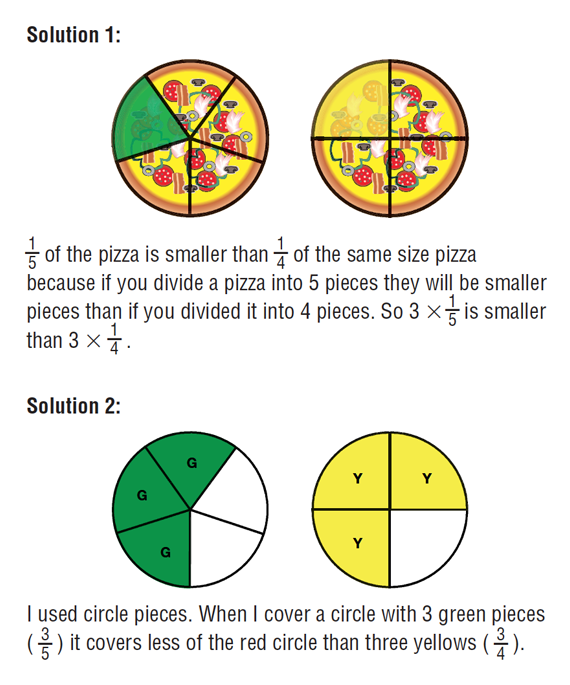
Review Fractions on a Number Line. Begin this lesson by posing the following problem.

Ask students to discuss this with a partner:

Which is smaller: 3/5 of a pizza or 3/4 of the same size pizza? How do you know?

After partners discuss this, ask several students to share their strategies with the class. Figure 1 shows two possible solution strategies.

Display the Fractions on Number Lines Chart page from the Student Guide Reference section. Explain that number lines can also be used to compare fractions. Fractions that are closer to zero on the number line are smaller.

Ask:

Which fraction is closer to zero, 3/5 or 3/4? (3/5)
What does this tell you about the size of 3/5 compared to the size of 3/4? (When the whole is the same, 3/5 is smaller than 3/4.)

A fraction with zero in the numerator and a whole number in the denominator is equal to zero. For example, 0/4 = 0. This makes sense: If you divide something into 4 equal parts and then take 0 of the parts, you will have taken nothing.

By definition, fractions cannot have a zero in the denominator. For example, 4/0 is not a fraction. One reason mathematicians chose to exclude zero denominators in defining fractions is that the denominator indicates the number of parts a whole is divided into and it doesn't make sense to divide something into zero parts. If you start with a whole, you cannot cut it up so that it has no parts at all.

Direct students to the Compare Fractions to Benchmarks pages in the Student Guide. The opening paragraphs show students how to use number lines to compare fractions and how to write number sentences comparing fractions using the less than (<) and greater than (>) signs. Question 1 provides practice using the number lines to compare fractions.

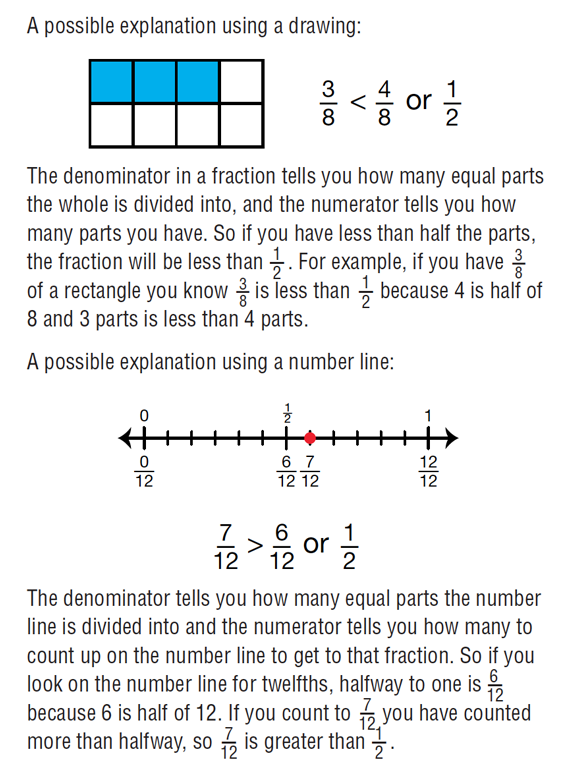
Compare Fractions to 1/2. In Question 2 of the Compare Fractions to Benchmarks pages in the Student Guide, students are directed to use 1/2 as a benchmark to compare fractions. Ask students to work in pairs and use the number lines on the chart to complete Question 2A. Sketch a three-column chart on a display with the headings: “< 1/2 ”, “= 1/2”, and “ > 1/2 ”. Ask several volunteers to put one fraction in each column using their answers to Question 2A.

Then discuss the second part of the question using these or similar prompts:

What patterns tell whether a fraction is less than, equal to, or greater than one-half? Use examples from the chart on the display to justify your thinking. (Possible response for the fractions less than 1/2: When fractions are less than 1/2 the numerator is less than half the denominator. For example, in the fraction 2/5, 2 is less than half of 5 so 2/5 is less than 1/2. Possible response for fractions equal to 1/2: When a fraction is equal to 1/2, the numerator is half of the denominator. For example, in the fraction 6/12 , 6 is half of 12 so 6/12 is equal to 1/2. Possible response for fractions greater than 1/2: When a fraction is greater than 1/2, the numerator is more than half of the denominator. For example, in the fraction 5/8, 5 is more than half of 8 so 5/8 is greater than 1/2.)
Think about what numerators and denominators tell you. Work with your partner to find an explanation to justify how these patterns work. Use tools such as fraction circle pieces, number lines, or drawings to help you. Use examples in your explanation.

Ask several students to share their explanations. Figure 2 shows one possible explanation using a drawing and one using a number line.

Students use their patterns to complete Question 2B. As students work, ask them how they decided whether the fractions were more or less than 1/2.

Compare Fractions to 0, 1/2, and 1. Use Question 3 to lead a similar discussion. Students identify, describe, and use patterns to compare fractions to one.

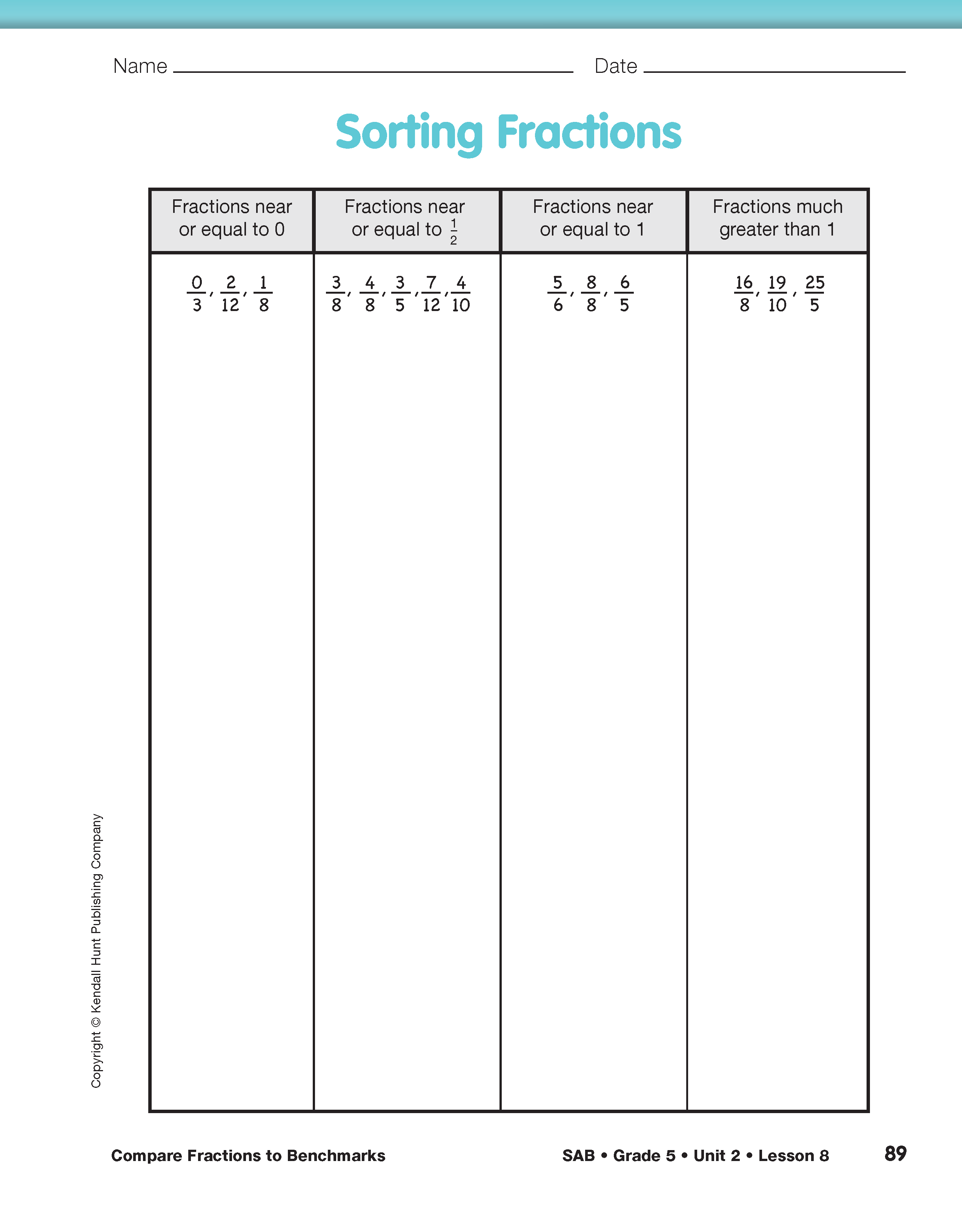
Question 4 asks students to sort fractions into a four-column data table on the Sorting Fractions page in the Student Activity Book. Encourage students to use the number lines to help them, as needed. After they have added the fractions in Question 4A to the table, students can compare their tables with those of their partners and can discuss any differences.

In Question 4B, students describe the similarities of fractions that are close to each benchmark. They discuss these questions in pairs or small groups. Then they share their ideas with the whole class. Their responses may include:

Fractions equal to zero have zero for a numerator.
Fractions near zero have small numerators but much larger denominators.
Fractions near 1/2 have numerators that are about half of their denominators.
Fractions equal to 1/2 have numerators that are exactly half of their denominators. The denominators are twice the numerators.
Fractions equal to 1 have the same numerator and denominator.
Fractions close to 1 have numerators that are almost the same as their denominators.
Fractions much greater than one have numerators that are much larger than their denominators.

Questions 4C–4D ask students to add fractions to their tables. After providing time to complete each of these questions, allow students to share their answers and strategies.

For example, ask:

How did you use the patterns to add 17/10 to your table? (Possible response: I knew that 17 is greater than 10 so that means it's greater than one.)

Question 5 asks students to use the benchmarks of 0, 1/2, and 1 to compare fractions. As students work, ask them which benchmarks they used and how they helped them decided which fraction was larger. Encourage them to refer back to the number lines as necessary.

For example, ask:

How did you decide which fraction was larger in Question 5A? Which benchmarks did you use? (Possible response: I knew that 5/12 is larger than 1/10 because 5/12 is close to 1/2 and 1/10 is close to 0.)

Assign the Use Benchmarks to Sort Fractions Homework in the Student Activity Book.