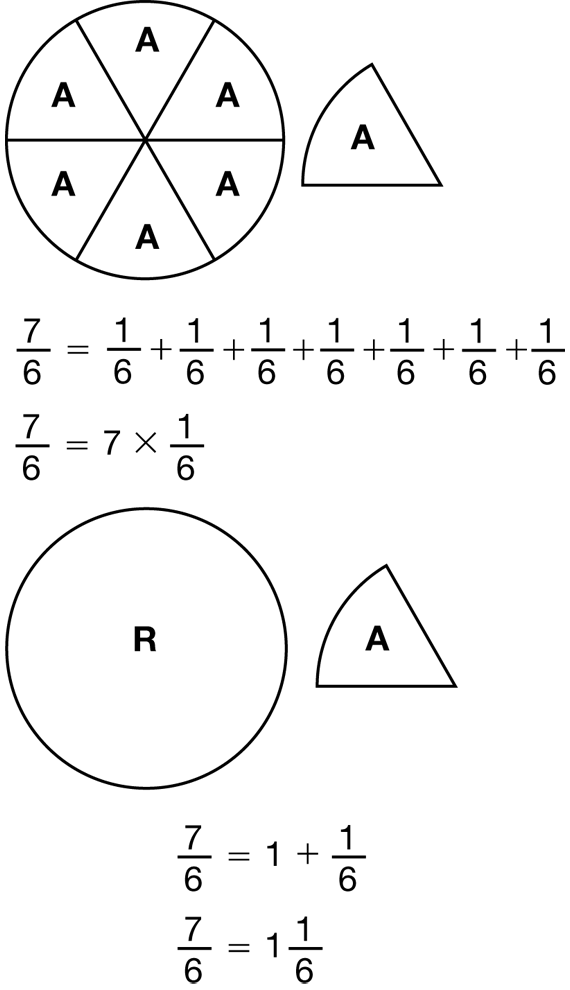
Begin with the diagrams in the Fractions Greater Than One section in the Student Guide. Draw these two figures on a display or build them with display fraction circle pieces. Ask students to write number sentences for each of your figures. Since students know that multiplication can be thought of as repeated addition, encourage them to write an addition sentence and a multiplication sentence for the improper fraction. They can write an addition sentence for the mixed number. Figure 4 shows 7/6 and 11/6 with number sentences.
Use the terms improper fraction and mixed number as you discuss the figures. An improper fraction is a fraction in which the numerator is greater than or equal to the denominator. A mixed number is a number made up of a whole number and a fraction. A proper fraction is a fraction that is less than one. The numerator is less than the denominator.
Have students study the diagrams of the improper fraction and the mixed number in the Student Guide.
- Does the diagram showing 5/3 and the diagram showing 12/3 represent the same quantity? Why or why not? (Possible response: Yes, they both represent the same quantity because the 3/3 in the first diagram is equal to the one whole in the second diagram. Both diagrams also have pieces representing 2/3.)
- What do you call a fraction that has a numerator that is equal to or greater than the denominator? (an improper fraction)
- What do you call a number that has a whole number and a fraction? (a mixed number)
- When a fraction's numerator is less than its denominator, what is that number called? (a proper fraction)
While working on Questions 9–15, students may need to work in groups of four in order to have enough fraction circle pieces.
To complete Questions 9–15, students use fraction circle pieces to model fractions greater than one and then write number sentences for the models. As they work, ask students to look for strategies that will help them write mixed numbers for improper fractions and improper fractions for mixed numbers when they do not have circle pieces available.
To guide their thinking, ask:
- When you change an improper fraction to a mixed number, how can you decide how many wholes you will have? (Possible response: You use the denominator to see into how many pieces each whole is divided. Then you divide the denominator into the numerator to see how many wholes there will be.)
- What happens to the numerator? (Possible response: The numerator will be less than the denominator, once all the whole numbers are taken out.)
- For 9/4, how many fourths make a whole? (4)
- How many wholes are there in 9/4? (2 wholes with 1/4 left over.)
- What mixed number represents the same quantity as 9/4? (21/4)
- When you change a mixed number into an improper fraction, what does the denominator tell you? (Possible response: It tells you into how many pieces each whole will be divided.)
- For the mixed number 22/3, into how many parts will each whole be divided? (3)
- How many total thirds are represented by the whole number 2? (6)
- What is the improper fraction that represents the same quantity as 22/3? (8/3)
Questions 16–17 ask students to explain their strategies to convert between improper fractions and mixed numbers. After giving students some time to think about their explanations, help them to develop procedures that are both meaningful and efficient by asking questions such as those contained in the Sample Dialog.

Teacher: Let's say you wanted to explain to your friend how to change 11/4 to a mixed number. How would you do that?
John: Well, you know the denominator has to stay the same. There are 4 fourths in one whole, so you need to know how many wholes are in 11/4.
Teacher: And how would you find that?
John: Four of the fourths is one whole [raising one finger], then 8 of the fourths makes two wholes [raising two fingers], and then there are 3 fourths left over. So, 2 and 3 fourths.
Teacher: Good, John. Did anyone use the word “subtract” in a strategy?
Ana: I would tell my friend to keep subtracting the bottom number from the top number and count how many times. Subtract four once and you have 7 left. Subtract four twice and you have 3 left. You can't subtract four again so the three is left over and then it's 3 fourths. Two and 3 fourths.
Teacher: That's right, Ana. And did anyone use the word “division” in a strategy?
Maya: I did. You just divide 11 by 4. That means you find how many groups of four are in 11. There are two groups, so you have 2. Then there is 3/4 of a group left over, so you have 2 and 3 fourths total.
In Questions 18–19 students practice using their favorite strategies from the class discussion to convert between improper fractions and mixed numbers. Students may complete unfinished questions at home.