Use the Single-Color Method with Circle Pieces. Introduce the example problem on the Find Fraction Sums 1 pages in the Student Activity Book. Before referring to the page, use the display set of circle pieces to demonstrate the problem. Display one yellow piece and one orange piece.
- What fraction addition problem do these pieces show? (1/4 + 1/3)
- Is the sum more than 1/2 or less than 1/2? How do you know? (It is more than 1/2 because it is larger than a pink piece.)
- Can you tell what the exact answer is easily by looking at the pieces? (Possible response: No, since the colors are different.)
- How can you make it so that the colors are the same? (Replace pieces so that they are all one color and so that they cover the yellow and orange piece exactly.)
- How can you find the right color to replace the pieces with? (Possible response: Try different colors until a color covers both pieces evenly.)
If it does not come up, suggest starting with orange and yellow. If one of the colors covers the other evenly, only one color needs to be replaced. For this problem, however, this single color-replacement method will not work. Students may recall from work on Question 5 that black covers both yellow and orange.
Demonstrate replacing pieces and ask:
- What is the sum? (7/12)
- How do you know? (Count the number of black pieces. There are 7. Since there are 12 black pieces in a whole circle, each piece is 1/12 of the whole circle.)
- What are some number sentences you could write for this sum? (1/4 + 1/3 = 7/12 or 3/12 + 4/12 = 7/12)
- Was your estimate correct? Is the sum more or less than 1/2? (a little more than 1/2)
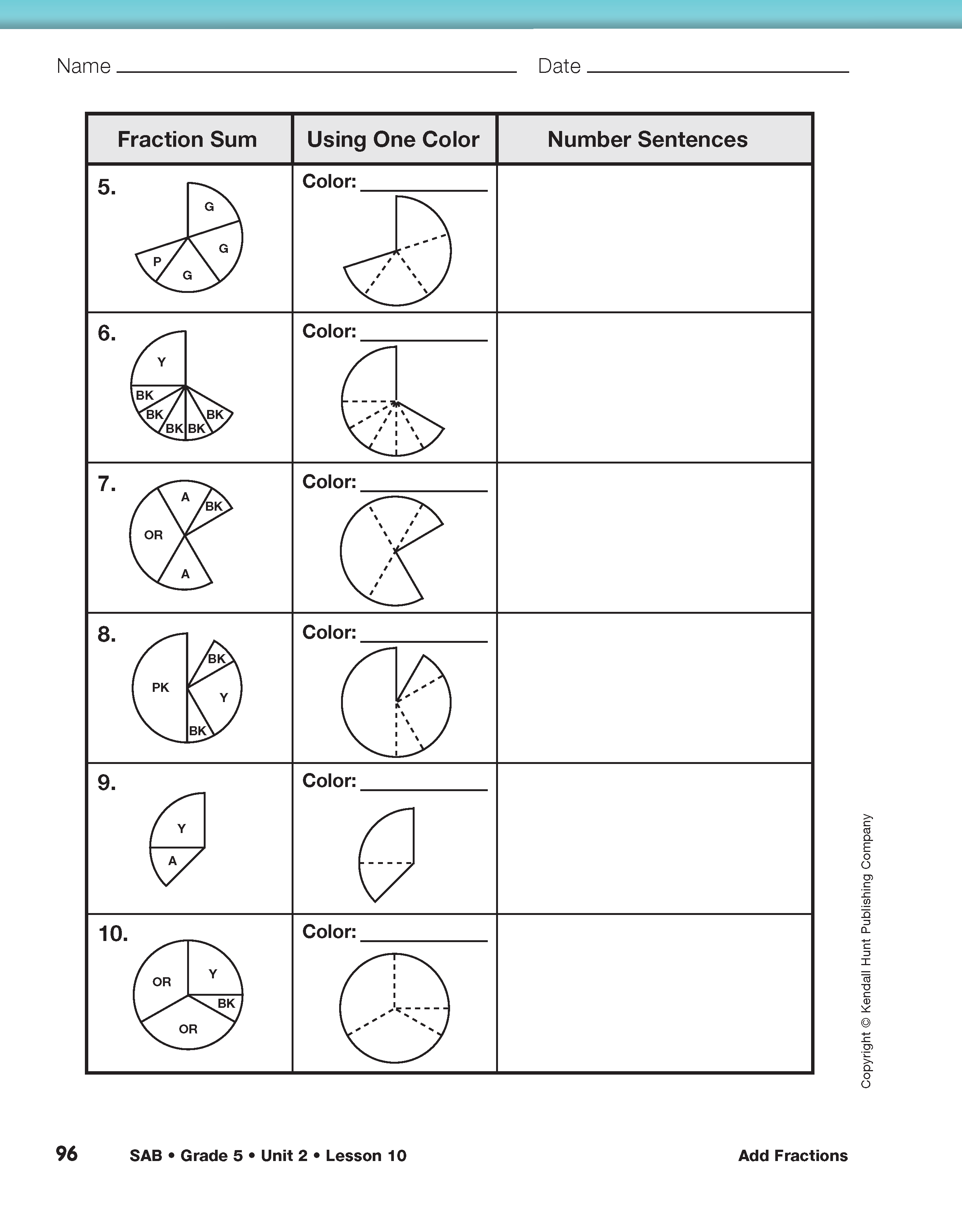
Display the first page of the Find Fraction Sums 1 pages in the Student Activity Book. Discuss the directions and ask students to complete Questions 1–10 with a partner using circle pieces. In the second column of the table, students draw a sketch to show how they replace the pieces with a single color. The dashed lines show where the original pieces are located in the unit circle. Students may use the lines as a guide for the sketch. Remind them to write the name of the replacement color in each box of the second column as in the example. As they are working, select pairs of students to display their work for two or three of the problems.
As students show their solutions, ask them to explain their thinking with questions such as the following:
- How did you decide which single color to use?
- What is the common denominator for the fractions you added?
- How do the number sentences relate to the circle pieces?

The instructions for the Find Fraction Sums 1–2 pages in the Student Activity Book ask students to find the sums by using the single-color method. This method eventually leads students to a structured procedure for finding common denominators (though this term is not used at this point). For some students, the consistent use of the single-color method may be helpful for building number sense with fractions. It may also help establish a consistent place to start for solving fraction sums.
At the same time, it is important to help students become flexible problem-solvers. Some students may already be thinking flexibly about fraction sums. For example, in the sample problem on the Find Fraction Sums 2 pages, students may notice that they can fill in a unit whole by placing two of the purple pieces with the five green pieces, leaving only one additional purple piece left over. Students should be encouraged to model and solve these problems in flexible ways as they are ready to do so. As students become comfortable with the single-color method, they should also be encouraged to think about solving problems using various strategies.
Find and Add Equivalent Fractions with Common Denominators. After discussing a few problems, ask students to read about Julia's solution to Question 2 on the Find Fraction Sums 1 pages in the Student Activity Book. Julia finds equivalent fractions with common denominators to add 1/2 + 1/6. Assign Questions 11–12 to provide practice with this method.
Upon completion, discuss Question 12 by having a volunteer demonstrate how to find fractions with common denominators to solve 1/4 + 1/6.
- Is Julia's method more like Kathy's method or Romesh's? Explain. (Julia's method of finding equivalent fractions with common denominators is like Romesh's single-color method. Both methods find common denominators to make adding easier.)
- To add 1/4 + 1/6 in Question 12, the common denominator 12 was found. Could Romesh have used 24ths instead? Explain. (Yes; By multiplying 1/4 by 6/6 and by multiplying 1/6 by 4/4, equivalent fractions for 1/4 and 1/6 can be found. 1/4 = 6/24 and 1/6 = 4/24.)
- What do you notice about 12 and 24? (12 and 24 are multiples of 4 and 6.)
- How do you know that the fractions 1/4, 3/12, and 6/24 are equivalent? (Possible response: I can use fraction circle pieces to show that 1/4 and 3/12 each covers the same amount of the circle. Then I imagine cutting each of three black twelfths into six pieces, or 6/24 to show that 6/24 covers the same part of a circle as 3/12 does.)
- Do you see a pattern in the fractions' denominators? (Yes; Possible response: 4, 12, and 24 are multiples of 4.)
- How do you know that the fractions 1/6, 2/12, and 4/24 are equivalent? (Possible response: I can use fraction circle pieces to show that one aqua piece can be replaced with 2 black pieces, so 1/6 is equivalent to 2/12. If I multiply 2/12 by 2/2, I find that 4/24 is equivalent.)
- Do you see a pattern in these fractions' denominators? (Yes; 6, 12, and 24 are multiples of 6.)
Relate the single-color method of replacing fraction circle pieces with pieces of all one color to that of finding common denominators.
- Was it easier to add fraction pieces of all one color or of different colors? (all one color)
- Was it easier to add fractions with like denominators or unlike denominators? Why? (Like; Possible response: Numerators tell the number of parts to add. Denominators tell the type of parts, so I just add the numerators together to find the sum.)
- Explain how Julia's method of finding common denominators is the same as replacing fraction circle piece with pieces of all one color. (It is just like using the single-color method. You trade pieces so you have all one color but you still cover the same amount of the circle. Instead of exchanging pieces, you exchange fractions, renaming them by finding equivalents. Instead of all the same color, you have all the same denominators.)
For more practice, ask students to use circle pieces, Julia's way, or another method to find the answers to the word problems in Questions 7–10 in the Student Guide.